
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Полные и неполные дифференциалы
Выше упомянули, что U – является функцией состояния подобно V, т.к. она зависит только от состояния системы.
Интегрирование дифференциальных функции состояния по любому произвольно выбранному пути дает просто разность между значениями этой функции в двух граничных точках. Пусть система переходит из состояния «a» в состояние «b».
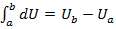
(1.9)
Поскольку этот интеграл не зависит от пути, то дифференциал функции состояния называется полным дифференциалом. Величины q и  не являются функциями состояния: интеграл от дифференциала этих величин при a -> b зависят от выбранного пути – это неполные дифференциалы.
не являются функциями состояния: интеграл от дифференциала этих величин при a -> b зависят от выбранного пути – это неполные дифференциалы.
Обозначим их 
Для работы: 
Совершенной при переходе из состояния a -> b
Запись  невозможна, так как произведённое количество работы зависит от пути перехода между состояниями a и b.
невозможна, так как произведённое количество работы зависит от пути перехода между состояниями a и b.
Если система поглощает бесконечно малое количество теплоты  и над ней совершается бесконечно малая работа
и над ней совершается бесконечно малая работа  , то соответствующее бесконечно малое изменение внутренней энергии
, то соответствующее бесконечно малое изменение внутренней энергии
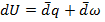
(1.10)
Таким образом сумма двух  может быть полным дифференциалом.
может быть полным дифференциалом.
Циклическим процессом называется процесс, когда система проходит через ряд стадий, которые в конце концов приводят её обратно в исходное состояние. Изменение внутренней энергии, т.к. dU – полный дифференциал
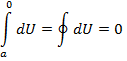
(1.11)
В общем случае  и
и 
Обратимые процессы
Обратимым называется процесс, который можно в любой момент заставить протекать в обратном направлении, изменив какую-нибудь независимую переменную на бесконечно малую величину.
Обратимый процесс часто определяют как ряд последовательных состояний равновесия. Такое представление часто используют как идеализацию реальных процессов.
Обратимые процессы очень важны для теории, потому что они дают наибольшую работу, которая может быть вообще получена при данном изменении от состояния 1 до состояния 2. Это как раз то количество работы, которое необходимо, чтобы вернуть систему в исходное состояние.
При необратимом процессе работы производится меньше, чем нужно затратить, чтобы вернуть систему в начальное состояние.
Пример:

При таком расширении газа в цилиндре давление его уменьшается пока не станет равным внешнему давлению, после этого поршень перестает двигаться. Следующее бесконечно малое уменьшение давления вызывает новое расширение газа на dV. Т.о. происходит ряд последовательных приращений V.
Во время любой отдельной стадии расширения давление в газе постоянно (с точностью до dP – бесконечно малое)
Работа, производимая на любой стадии, равна внешнему давлению, x на «-dV».
Общее количество работы, которое можно получить при обратимом расширении газа от начального V1 до конечного V2 и равно:
 на любой стадии
на любой стадии
(1.12)
Поскольку на любой стадии расширения газ находится при равновесном давлении (с точностью до dP) можно подставить в формулу выражение для зависимости давления от V, полученное из равновесных данных равенство.
Если бы газ расширялся быстро, такую подстановку уже нельзя было бы сделать.
Только в том случае, когда расширение проводится обратимо при T=const, получается достаточное количество энергии, чтобы осуществить обратный процесс сжатия газа до исходного состояния.
Пример:
Вывести формулу для максимальной работы, получаемой при изотермическом расширении идеального газа в обратимом процессе.
T=const; P=nRT/V, подставим в (1.12)

Если количество газа составляет 1 моль, то 
Тогда

Численный пример:
Какова работа, производимая при обратимом расширении 1 моля идеального газа при 00С от 2.24 до 22.4л?

(273.15K)lg=-1250 кал/моль=-2.303[8.314Дж/(К*моль)]
(273.15К)lg10=-5230Дж/моль
Другой пример обратимого процесса – испарение жидкости при изменении T на бесконечно малую величину на каждой стадии процесса в следующей схеме эксперимента:
Жидкость в цилиндре снабженном поршнем, вся система находится в равновесии при Tрезервуара=Тр1
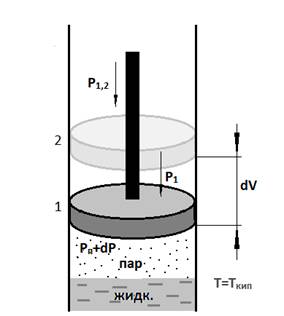
Пусть Тр1+dT ->P+dP -> поршень поднимается; V увеличивается, следовательно давление падает, испаряется дополнительное количество жидкости. Как только давление пара над жидкостью станетравным внешнему давлению поршень остановится.
Давление таким образом поддерживается постоянным. Теплота, за счет которой происходит испарение иподдерживается T=const, поступает из теплового резервуара.
Этот процесс поглощения теплоты и совершения внешней работы обратим, поскольку в любой момент испарение можно приостановить, понизив Т на бесконечно малую величину или повысив Pвнешнее на бесконечно малую величину так, чтобы Pвнутр.=Pвнеш.
Если еще увеличить Pвнеш. На бесконечно малую величину, то пар начнет конденсироваться, при этом в тепловой резервуар будет возвращаться теплота, поглощенная при испарении.
[Задача 4? ]
Не нашли, что искали? Воспользуйтесь поиском: