
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретическая часть.
Для
дисциплины «Математика»
Саратов 2016
Содержание: ст.
| Практическая работа. Функция одной переменной. Свойства функций. | |
| Практическая работа. Вычисление производных алгебраических функций. Вычисление производных сложных и обратных функций. | |
| Практическая работа. Предел и непрерывность функции. | |
| Практическая работа.Вычисление предела функции, раскрытие простейших неопределенностей. | |
| Практическая работа. Исследование функций посредством производной и построение графиков. | |
| Практическая работа. Дифференцирование функций. | |
| Практическая работа. Нахождение неопределённых интегралов. | |
| Практическая работа. Решение задач прикладного характера с применением определенного интеграла. | |
| Практическая работа. Элементы комбинаторики. | |
| Используемая литература |
ПРАКТИЧЕСКАЯ РАБОТА. Функция одной переменной. Свойства функций.
ЦЕЛЬ РАБОТЫ:
1. Скорректировать знания, умения и навыки в теме: «Свойства функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности студентов.
Методические указания для проведения практической работы.
Теоретическая часть.
Ответить на контрольные вопросы:
а) Что называется функцией?
б) Что такое естественная область определения функции?
в) Какая функция называется четной, нечетной?
г) Как найти точки пересечения графика функции с осями координат?
 Понятие функции. Пусть Х и У – два множества действительных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число
Понятие функции. Пусть Х и У – два множества действительных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число 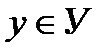 , то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:
, то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:  .
.
Множество Х- называют областью определения функции, а множество У, состоящее из всех чисел вида 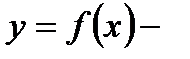 множеством значений функции.
множеством значений функции.
Если у является функцией от х, то пишут 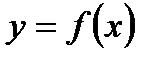 . Область определения обозначается через
. Область определения обозначается через 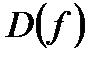 , а множество значений – через
, а множество значений – через 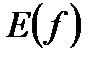 .
.
 Основные элементарные функции. Основными элементарными функциями называют следующие функции:
Основные элементарные функции. Основными элементарными функциями называют следующие функции:
1) степенная функция  ,
, 
2) показательная функция 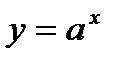 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 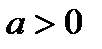 ,
, 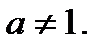
3) логарифмическая функция 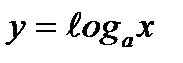 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 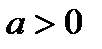 ,
, 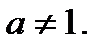
4) тригонометрические функции: 
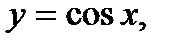

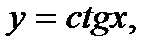

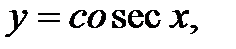
5) обратные тригонометрические функции: 

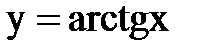
 ,
,  ,
, 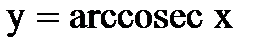 .
.
Элементарными называются функции, получающиеся из основных элементарных функций с помощью четырёх арифметических действий и применённых конечное число раз.
Графиком функции 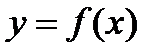 называется множество точек плоскости хОу с координатами
называется множество точек плоскости хОу с координатами  , где
, где 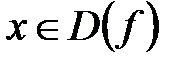 .
.
Функция 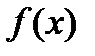 , область определения которой симметрична относительно нуля, называется чётной, если
, область определения которой симметрична относительно нуля, называется чётной, если 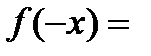
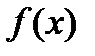 для
для 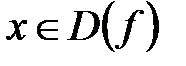 и нечётной, если
и нечётной, если 
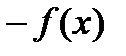 ,
, 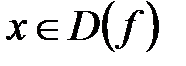 .
.
Произведение двух нечетных функций является четной функцией.
Функция 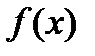 называется периодической, если существует положительное число Т такое, что при
называется периодической, если существует положительное число Т такое, что при 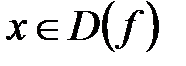 и
и  выполняется равенство
выполняется равенство 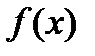 =
=  .
.
Решение заданий типового варианта практической работы
Пример 1. Найти область определения функции 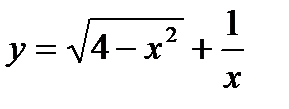 .
.
Решение. Данная функция определена, если  и
и 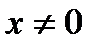 . Решаем эту систему:
. Решаем эту систему:

| -2 |
| - |
| - |
| + |
Рис. 1.
Ясно, что искомое неравенство имеет место при 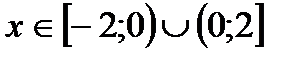 , значит, полученное множество есть область определения данной функции.
, значит, полученное множество есть область определения данной функции.
Пример 2. Установить чётность или нечётность функции 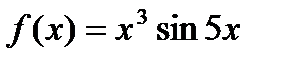 .
.
Решение. Для данной функции область определения симметрична относительно нуля: 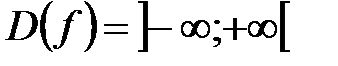 .
.
Заменяя х на –х, получим 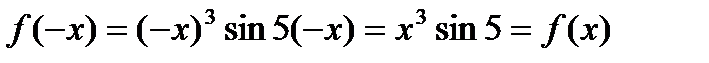 , т.е.
, т.е. 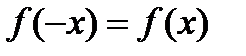 . Итак, данная функция чётная.
. Итак, данная функция чётная.
Пример 3. Найти основной период функции  .
.
Решение. Так как основной период функции 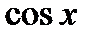 есть
есть  , то основной период функции
, то основной период функции 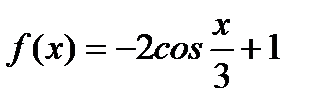 есть
есть 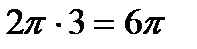 , т.е.
, т.е. 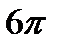 .
.
Не нашли, что искали? Воспользуйтесь поиском: