
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вычисление производных алгебраических функций. Вычисление производных сложных функций.
Вариант 1.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
1)  ; 2)
; 2)  ; 3)
; 3) 
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
2. Решите уравнение  , если
, если  .
.
3. Решите неравенство  , если
, если  .
.
4. Материальная точка движется прямолинейно по закону  . Через сколько секунд после начала движения точка остановится?
. Через сколько секунд после начала движения точка остановится?
Вариант 2.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 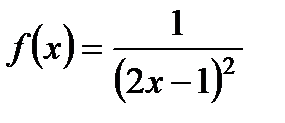 ; 5)
; 5)  ; 6)
; 6)  .
.
2. Решите уравнение  , если
, если  .
.
3. Решите неравенство  , если f(x) =
, если f(x) =  .
.
4. По прямой движутся две материальные точки по законам  и
и  . В каком промежутке времени скорость первой точки больше скорости второй?
. В каком промежутке времени скорость первой точки больше скорости второй?
Вариант 3.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
1)  ; 2)
; 2)  ; 3)
; 3) 
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
2. Решите уравнение  , если
, если  .
.
3. Найдите х, при котором  , если
, если  .
.
4. Тело движется по прямой согласно закону  . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени  .
.
Вариант 4.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
2. Решите уравнение  , если
, если  .
.
3. Решите неравенство  , если
, если  .
.
4. Тело движется по прямой согласно закону  . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени  .
.
Не нашли, что искали? Воспользуйтесь поиском: