С) Цепь с емкостным сопротивлением.

Конденсатор, имеющий емкость С, в цепи переменного тока обладает определенным сопротивлением, обусловленным свойством конденсатора накапливать и отдавать электрическую энергию.

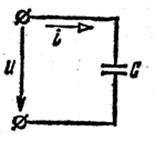
Рисунок 3.8 Электрическая цепь переменного тока с идеальным конденсатором

Сопротивление в цепи с емкостным сопротивлением является реактивным емкостным. Оно обозначается X_С и измеряется в Омах.

(3.8)

где ω – угловая частота, с^-1

С– емкость конденсатора, Ф

В цепи с идеальным конденсатором угол сдвига фаз между током и напряжением составляет φ = 90⁰.

Рисунок 3.9 Временные диаграммы тока и напряжения для цепи с идеальным конденсатором

Рисунок 3.10 Векторная диаграмма для цепи с идеальным конденсатором

В цепи с емкостью нет преобразования электрической энергии в тепловую. Происходит лишь обмен энергией между конденсатором и источником питания. Мощность в цепи с емкостным сопротивлением является реактивной емкостной. Она обозначается Q _С и измеряется в «вар».

Реактивную мощность, рассеиваемую на идеальном конденсаторе, можно рассчитать по формулам:

Q_С = U · I (3.9)

Q_С = I² · X_с (3.10)

Неразветвленная электрическая цепь переменного тока

Рассмотрим последовательное соединение активного индуктивного и емкостного сопротивлений.

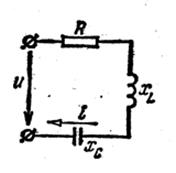
Рисунок 3.11 Неразветвленная электрическая цепь переменного тока

При последовательном соединении вектор приложенного к цепи напряжения равен сумме векторов падений напряжения на участках цепи, а ток на всех участках цепи имеет одно и то же значение.

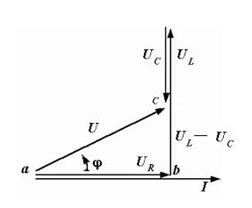
Рисунок 3.12 Векторная диаграмма для неразветвленной цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений

Построение векторной диаграммы начинают с вектора тока, который располагается горизонтально. Вектора напряжений на участках цепи откладывают последовательно один за другим с учетом угла сдвига фаз. В результате сложения векторов U_R, U_L, U_C получен вектор приложенного напряжения U.

Рассматривая векторную диаграмму, можно выделить прямоугольный треугольник напряжений.

Рисунок 3.13 Треугольник напряжений для неразветвленной цепи переменного тока

Из треугольника напряжений по теореме Пифагора можно записать:

(3.11)

Разделив обе части уравнения на I, получим формулу вычисления полного сопротивления неразветвленной цепи с последовательным соединением активного, индуктивного и емкостного сопротивлений.

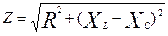(3.12)

Это уравнение иллюстрируется треугольником сопротивлений

Рисунок 3.14 Треугольник сопротивлений для неразветвленной цепи переменного тока

Из треугольника сопротивлений можно определить коэффициент мощности cos φ, который показывает, какая часть потребляемой цепью мощности приходится на активную составляющую.

(3.13)

Умножив все стороны треугольника напряжений на ток I, получим подобный треугольник мощностей, он также будет скалярным, так как мощность – величина скалярная.

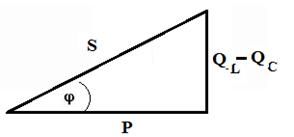
Рисунок 3.15 Треугольник мощностей для неразветвленной цепи переменного тока

Гипотенуза треугольника соответствует полной мощности, потребляемой цепью от источника питания. Она обозначается S и измеряется в Вольт-Амперах [ ВА ]. Формула для определения полной мощности имеет вид:

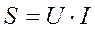(3.14)

Прилежащий катет треугольника соответствует активной мощности, выделяемой на активных сопротивлениях. Она обозначается P и измеряется в Ваттах [Вт ]. Формула для определения активной мощности имеет вид:

(3.15)

Противолежащий катет треугольника соответствует реактивной мощности, накапливаемой реактивными сопротивлениями. Она обозначается Q и измеряется в вольт – амперах реактивных [вар]. Формула для определения реактивной мощности имеет вид:

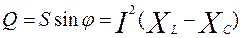(3.16)

Величина тока в цепи определяется по закону Ома

(3.17)

Не нашли, что искали? Воспользуйтесь поиском: