Подпространство топологического пространства

Теорема 1. Пусть A - подмножество в топологическом пространстве (X, t). И пусть t_A - семейство пересечений множества A со всеми элементами из t: t_A={U|U=AÇV,VÎt}. Тогда t_A - топология на A.

Доказательство. Так как Æ ÇA= Æ и XÇA=A, то аксиомы 1 и 2 выполняются. Далее, пусть U₁ и U₂ принадлежат t_A, где U₁=V₁ÇA, U₂=V₂ÇA, V₁,V₂Ît. Тогда U₁ÇU₂=(V₁ÇA)Ç(V₂ÇA)=V₁ÇV₂ÇA, так как V₁ÇV₂Ît, то U₁ÇU₂Ìt_A и третья аксиома тоже выполняется.

Пусть теперь U_lÌt_A, где индекс l пробегает некоторое множество L, U_l=V_lÇA, V_lÎt. Рассмотрим . Имеем 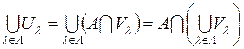, так как , то Ît_A и четвертая аксиома тоже выполняется. ÿ

Определение. Топология t_A, определенная в теореме 1, называется топологией, индуцированной на множестве A топологией t, а топологическое пространство (A, t_A) называется подпространством топологического пространства (X, t).

Замечание 1. Любое подмножество топологического пространства всегда рассматривается как топологическое подпространство исходного пространства.

Теорема 2. Если топологическое пространство имеет счетную базу, то любое его подпространство имеет счетную базу.

Теорема 3. Если пространство (X, t) имеет топологию, индуцированную метрикой r, то любое его подпространство (A, t_A) имеет топологию t_A, индуцированную метрикой r|_A.

Определение. Свойство топологического пространства называется наследуемым, если оно сохраняется при переходе от данного пространства к любому его подпространству.

Следствие из теоремы 2. Счетность базы - наследуемое свойство.

Не нашли, что искали? Воспользуйтесь поиском: