Решение игр вида 2хn и mх2

Методы решения конечных игр

Решение игр вида 2хn и mх2

Графо-аналитический метод.

У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2, которую мы уже умеем решать. Поэтому игры 2 х n и m х 2 решают обычно графоаналитическим методом.
Рассмотрим решение матричной игры на примере.
Пример.

Решение.

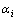
	1	4	7	1
	6	3	2	2
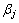
	6	4	7	2 4

a = 2, b=4, , поэтому игра не имеет седловой точки, и решение должно быть в смешанных стратегиях.
1. Строим графическое изображение игры.

Если игрок B применяет стратегию В₁, то выигрыш игрока A при применении стратегии А₁ равен а₁₁ = 1, а при использовании А₂ выигрыш равен а₂₁ = 6, поэтому откладываем отрезки А₁В₁ = 1, А₂В₁^′ = 6 на перпендикулярах в А₁ и А₂ и соединяем их отрезком. Аналогично для стратегий В₂ и В₃ строим отрезки В₂ В₂^′ и В₃ В₃^′.
2. Выделяем нижнюю границу выигрыша В₁М N В₃^′ и находим наибольшую ординату этой нижней границы, ординату точки М, которая равна цене игрыγ.
3. Определяем пару стратегий, пересекающихся в точке оптимума М.
В этой точке пересекаются отрезки В₂В₂^′ и В₁В₁^′, соответствующие стратегиям В₁ и В₂ игрока B. Следовательно, стратегию В₃ ему применять невыгодно. Исключаем из матрицы третий столбец и решаем игру 2 x 2 аналитически:

; ; .
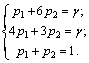
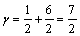
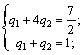
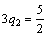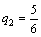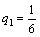Ответ: γ = 7/2; P_A = (1/2; 1/2); Q_B = (1/6; 5/6; 0). Правила решения игры 2xn

♦ строится графическое изображение игры;
♦ выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы, которая равна цене игры γ;
♦ определяется пара стратегий, пересекающихся в точке оптимума M. Эти стратегии являются активными стратегиями игрока B. Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них;
♦ решается полученная игра 2x2.
Решение игры m x2 осуществляется аналогично. Вместо пункта 2 применяется;
♦ выделяется верхняя граница выигрыша, и на ней находится точка оптимума с наибольшей ординатой.
Пример.

Решение.

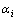
	0,4	1,0	0,4
	0,5	0,5	0,5
	1,0	0,3	0,3
	0,8	0,3	0,3
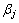
	1,0	1,0	0,5 1,0

a= 0,5, b= 1,0. Седловой точки нет.
1. строим графическое изображение игры относительно игрока В.
Если А применяет А₁, то при использовании игроком В стратегии В₁ выигрыш игрока А равен 0,4, а выигрыш А при стратегии В₂ равен 1,0, поэтому на перпендикулярах строим такие отрезки. Видно, что стратегия А₄ заведомо невыгодная по сравнению со стратегией А₃ (выигрыш меньше).
2. Выделяем верхнюю границу выигрыша А₃NА₁^′; точка с наименьшей ординатой – N.
3. В этой точке пересекаются отрезки А₁А₁^′ и А₃А₃^′, соответствующие активным стратегиям А₁ и А₃. Стратегия А₂ не является активной, поэтому из матрицы исключаем вторую и четвертую строки: .

4. решаем игру:

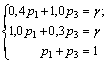
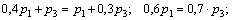
13p₃ = 6; p₃ =6/13; p₁ = 7/13

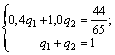
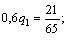
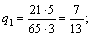
q₂ = 6/13.
Ответ: γ = 44/65; P_A = (7/13; 0; 6/13; 0); Q_B = (7/13; 6/13).

Примечание: Игроку А не выгодно отклоняться от спектра своих активных стратегий.

Игры с "природой"

Термин "природа" в теории игр понимается в широком смысле. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и т.п. процессы, которые сопровождают экономическую деятельность. Под "природой" может также пониматься рынок, противостоящий предпринимателю, конкурирующая среда, монополия и т.п. "Природа" может выступать как антагонистическая сторона, а может как кооперативная среда. "Природа" в виде природных процессов, как часть экономики, не стремиться "специально" навредить предпринимателю, но она несёт определённый урон от его экономической деятельности и этот "проигрыш"для неё должен быть минимален, если, вообще, без него для окружающей среды нельзя обойтись. Игрок A в таких играх - это экономические субъекты, а игрок B - это "природа". Откуда средства у физической "природы"? Проигрыш игрока B, физической "природы", должен компенсироваться из вне, например, государственными дотациями либо заложенными в инвестиционные проекты средствами на возобновление природных ресурсов. Знание оптимальных стратегий "природы" позволяет определить наиболее неблагоприятные условия для игрока A (предпринимателя), которые его ожидают ("надейся на лучшее, но готовься к худшему"), и оценить необходимые ресурсы на восстановление природных ресурсов, дающих ему возможность получить гарантированный доход.

Если "природа" подразумевает конкурентную среду - то проигрыш второго игрока есть цена борьбы с конкурентами на рынке.

Перейдём к примерам содержательных постановок задач игры с "природой".

Не нашли, что искали? Воспользуйтесь поиском: