
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Антагонистические игры
Пример 1. (Планирование посевов). Фермер, имеющий ограниченный участок земельных угодий, может его засадить тремя различными культурами A1, A2, A3. Урожай этих культур зависит главным образом от погоды ("природы"), которая может находиться в трёх различных состояниях: B1, B2, B3. Фермер имеет информацию (статистические данные) о средней урожайности этих культур (количество центнеров культуры, получаемого в одного гектара земли) при трёх различных состояниях погоды, которая отражена в таблице:
| Виды культур | Возможные состояния погоды | Цены | ||
| Засуха B1 | Нормальная B2 | Дождливая B3 | ||
| A1 | ||||
| A2 | ||||
| A3 |
Тогда матрица доходов (платёжная матрица) фермера A имеет вид:

Элемент матрицы A - (aij) показывает, какой доход может получить фермер с одного гектара земли, если он посеет культуру i ( i =1, 2, 3), а погода будет находиться в состоянии j (j = 1, 2, 3).
Необходимо определить пропорции, в которых фермер должен засеять имеющийся участок земли, чтобы получить максимальный гарантированный доход вне зависимости от того, какие погодные условия будут реализованы.
Данная задача может быть сведена к антагонистической игре. В данном случае в качестве первого игрока выступает фермер, а в качестве второго игрока - природа. Будем предполагать, что природа, как игрок, может вести себя таким образом, чтобы максимально навредить фермеру, преследуя тем самым противоположные интересы (эти предположения позволяют оценить тот доход, который он может получить в том случае, если погодные условия будут для него максимально неблагоприятные). В этом случае фермер имеет в своём распоряжении три чистые стратегии:
· первая чистая стратегия предполагает, что весь участок земли буде засеян культурой A1;
· вторая чистая стратегия предполагает, что весь участок земли будет засеян культурой A2;
· третья чистая стратегия предполагает, что весь участок будет засеян культурой A3.
Как игрок, природа может также использовать три возможные стратегии:
· засушливую погоду, которая соответствует первой чистой стратегии B1;
· нормальную погоду, которая соответствует второй чистой стратегии B2;
· дождливую погоду, которая соответствует третьей чистой стратегии B3.
Решение
1. Проанализируем платёжную матрицу A.

Матрица A не имеет доминируемых стратегий и не может быть упрощена.
2. Проверим, имеет ли данная игра седловую точку.
Найдём нижнюю и верхнюю цену игры:
V*=maxi minjaij = 50.
V*=minjmaxiaij = 100.
Поскольку V* ≠V*, то данная антагонистическая игра не имеет седловой точки и решения в чистых стратегиях.
3. Решение игры следует искать в смешанных стратегиях. Сведём игровую задачу к задаче линейного программирования. Если первый игрок - фермер - применяет свою оптимальную смешанную стратегию P*, а второй игрок - природа - применяет последовательно свои чистые стратегии, то математическое ожидание дохода, который фермер может получить со своего участка, будет не меньше цены игры V. Следовательно, должна выполняться следующая система неравенств:

Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:
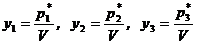 .
.
В результате получим новую систему неравенств:

Разделим равенство:
p*1 + p*2 + p*3 = 1
на V, получим, что новые переменные y1, y2, y3 удовлетворяют условию:
y1 + y2 + y3 = 1/V
Поскольку цель первого игрока - максимизация его выигрыша, а математическое ожидание его выигрыша не меньше цены игры, то первый игрок будет стремиться максимизировать цену игры, которая эквивалентна минимизации величины 1/V.
Итак, для первого игрока (фермера) задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:
найти минимум функции F = y1 + y2 + y3
при следующих функциональных ограничениях:

и прямых ограничениях:
y1 ≥ 0, y2≥ 0, y3≥ 0
Переходим ко второму игроку, к природе. Если второй игрок - природа - будет применять свою оптимальную смешанную стратегию Q*,а первый игрок - фермер будет последовательно применять свои чистые стратегии, то математическое ожидание проигрыша второго игрока будет не больше цены игры. Следовательно, должна выполняться следующая система неравенств:

Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:
 .
.
В результате получим новую систему неравенств:

Разделим равенство:
q*1 + q*2 + q*3 = 1
на V, получим, что новые переменные q1, q2, q3 удовлетворяют условию:
q1 + q2 + q3 = 1/V
Поскольку цель второго игрока - природы - минимизация его проигрыша, а математическое ожидание его проигрыша не больше цены игры, то второй игрок будет стремиться минимизировать цену игры, которая эквивалентна максимизации величины 1/V.
Итак, для второго игрока (природы) задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:
найти максимум функции F/ = x1 + x2 + x3
при следующих функциональных ограничениях:

и прямых ограничениях:
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
Таким образом, для того чтобы найти оптимальную смешенную стратегию второго игрока, необходимо также решить задачу линейного программирования.
Задачи обоих игроков свелись к паре двойственных задач линейного программирования:
| Задача второго игрока минимизация проигрыша V | Задача первого игрока максимизация выигрыша V |
| Целевая функция | |
F/ = x1+x2+x3 =   → max → max
| F = y1+y2+y3 =  → min → min
|
| Функциональные ограничения | |

| 
|
| Прямые ограничения | |
| x1 ≥ 0, x2 ≥ 0, x3 ≥ 0 | y1 ≥ 0, y2 ≥ 0, y3 ≥ 0 |
Задача первого игрока решается симплекс-методом. Результаты счёта:
| у1 = | 0,01 | p1 = | 0,67 |
| у2 = | p2 = | 0,00 | |
| у3 = | 0,005 | p3 = | 0,33 |
| F = | 0,015 | V = | 66,67 |
Задача второго игрока решается также симплекс-методом. Результаты счёта:
| x1 = | 0,005 | p1 = | 0,33 |
| x2 = | p2 = | 0,00 | |
| x3 = | 0,01 | p3 = | 0,67 |
| F = | 0,015 | V = | 66,67 |
Выводы. В соответствии с полученными результатами фермеру гарантирован средний доход в размере 66,67 единиц с каждого гектара используемой под культурами земли при самых неблагоприятных условиях. Оптимальная стратегия для него - выращивание двух культур, A1 и A3, причём, под первую культуру ему следует отвести 0,67 часть всей земли, а под третью культуру 0,33 часть всей земли.
Природа "грозит" фермеру жарой 0,33 часть сезона возделывания культур и 0,67 часть сезона дождями.
Пример 2. (Планирование выпуска продукции при разных состояниях природы - рынка спроса)
Предприятие может выпускать 4 вида продукции: A1, A2, A3, A4, получая при этом прибыль. Её величина определяется состоянием спроса (природой рынка), который может находиться в одном из четырёх возможных состояний: B1, B2, B3, B4. Зависимость величины прибыли от вида продукции и состояния рынка представлено в таблице:
| Виды продукции | Возможные состояния рынка спроса | |||
| B1 | B2 | B3 | B4 | |
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
Платёжная матрица имеет вид:

Элемент матрицы A - { aij } характеризует, какую прибыль может получить предприятие, если оно будет выпускать i - й вид продукции(i =1, 2, 3, 4) при j-м спросе(j = 1, 2, 3, 4).
Необходимо определить оптимальные пропорции выпускаемых предприятием видов продукции, продажа которой обеспечила бы ему максимально возможную выручку вне зависимости от того, какое состояние спроса будет реализовано
Эта задача может быть сведена к антагонистической игре.
В данном случае в качестве первого игрока выступает предприятие, а в качестве второго игрока - природа, которая влияет на состояние спроса и может сделать его максимально неблагоприятным для предприятия. Будем предполагать, что природа, как игрок, будет вести себя таким образом, чтобы максимально навредить предприятию, преследуя тем самым противоположные интересы.
В этом случае конфликт двух сторон может характеризоваться, как антагонистический, а использование модели этого конфликта позволяет предприятию. оценить выручку, которую оно может получить вне зависимости от того, какое состояние спроса будет реализовано.
Выступая в качестве первого игрока, предприятие может использовать четыре стратегии:
· первую чистую стратегию, соответствующую выпуску предприятием только продукции A1
· вторую чистую стратегию, соответствующую выпуску предприятием только продукции A2
· третью чистую стратегию, соответствующую выпуску предприятием только продукции A3
· четвёртую чистую стратегию, соответствующую выпуску предприятием только продукции A4
Выступая в качестве второго игрока, природа может использовать также четыре стратегии:
· первую чистую стратегию, при которой реализуется состояние спроса B1;
· вторую чистую стратегию, при которой реализуется состояние спроса B2;
· третью чистую стратегию, при которой реализуется состояние спроса B3;
· четвёртую чистую стратегию, при которой реализуется состояние спроса B4.
Решение
1. Проанализируем платёжную матрицу A.

Матрица A не имеет доминируемых стратегий и не может быть упрощена.
2. Проверим, имеет ли данная игра седловую точку.
Найдём нижнюю и верхнюю цену игры:
V*=maxi minj aij = 3.
V*=minj maxiaij = 4.
Поскольку V* ≠V*, то данная антагонистическая игра не имеет седловой точки и решения в чистых стратегиях.
Решение игры следует искать в смешанных стратегиях. Сведём рассматриваемый антагонистический конфликт к прямой и двойственной задаче линейного программирования.
Если первый игрок - предприятие - применяет свою оптимальную смешанную стратегию P*, а второй игрок - природа - применяет последовательно свои чистые стратегии, то математическое ожидание дохода, который предприятие может получить, будет не меньше цены игры V.
И наоборот, если второй игрок - природа - будет применять свою оптимальную смешанную стратегию Q*, а первый игрок - предприятие будет последовательно применять свои чистые стратегии, то математическое ожидание проигрышавторого игрока будет не больше цены игры. Следовательно, должна выполняться следующая система неравенств:
| Задача второго игрока минимизация проигрыша V | Задача первого игрока максимизация выигрыша V |
| Целевая функция | |
F/ = x1+x2+x3+x4 =  → max → max
| F = y1+y2+y3+y4 =  → min → min
|
| Функциональные ограничения | |

| 
|
| Прямые ограничения | |
| x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0 | y1 ≥ 0, y2 ≥ 0, y3 ≥ 0, y4 ≥ 0 |
Применяя симплекс-метод для решения задачи первого игрока, получим:
Y*= (y1* = 0,182; y2* = 0; y3* = 0; y4* =0,091)
F= y1*+ y2*+ y3*+y4*= 0,273
Из соотношения y1*+ y2*+ y3*+y4*=1/V найдём V:

Из соотношений:

Найдём:
p*1 = y*1V = 0,67, p*2 = y*2V = 0, p*3 = y*3V = 0, p*4 = y*4V =0,33
Окончательно имеем:
Р* = (р*1 =0,67; р*2 = 0; р*3 = 0; р*4 = 0,33), V = 3.67
На основании решения, найденного для двойственной задачи линейного программирования, найдём решение исходной задачи - задачи второго игрока:
X*= (x1* = 0,121; x2* =0,121; x3* = 0,03; x4* = 0)
F/ = x1*+ x2*+ x3*+x4*= 0,273
Из соотношения x1*+ x2*+ x3*+x4* = 1/V найдём V:

Из соотношений:
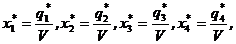
Найдём:
q*1 = x*1V = 0,445, q*2 = x*2V = 0,444, q*3 = x*3V = 0,111, q*4 = x*4V = 0.
Окончательно имеем:
Q*= (q*1= 0,445; q*2=0,444; q*3= 0,111; q*4= 0), V = 3.67
Не нашли, что искали? Воспользуйтесь поиском: