
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятие о методе динамического программирования
Лекция 5 Задачи динамического программирования
1. Понятие о методе ДП
2. Задачи, решаемые методами динамического программирования
Понятие о методе динамического программирования
Динамическое программирование – это особый метод поиска оптимального варианта управления (последовательности действий) среди n–мерных вариантов путем декомпозиции задачи оптимизации на n этапов, каждый из которых представляет подзадачу относительно одной переменной.
Этот метод специально приспособлен к многошаговым (многоэтапным) операциям. Управление таким процессом состоит из выбора на каждом этапе одного из возможных вариантов действий. Совокупность (последовательность) вариантов действий для каждого этапа представляет собой стратегию проведения операции (управление операцией):
U = (u1,u2, …, um),
где U – управление операцией в целом; i – управление на i –м шаге операции.
В задаче динамического программирования требуется найти такое оптимальное управление U*, при котором W(U*) = max {W(U)}, где  . Как мы заметили, интегральный критерий является аддитивным. В некоторых случаях он может быть мультипликативным, например, когда целевая функция имеет смысл вероятности наступления какого-либо события.
. Как мы заметили, интегральный критерий является аддитивным. В некоторых случаях он может быть мультипликативным, например, когда целевая функция имеет смысл вероятности наступления какого-либо события.
Модели динамического программирования могут быть как дискретными, так и непрерывными.
В основе моделей ДП лежит принцип оптимальности, выраженный математически в виде функциональных уравнений Беллмана. Р. Беллман (1952) впервые широко применил метод ДП для решения ряда оптимизационных задач в технике, экономике и исследовании операций. Строгое математическое обоснование метода ДП в 50-е годы было дано академиком Л. С. Понтрягиным и его учениками по математической теории управляемых процессов.
Метод динамического программирования можно применять для нахождения оптимального управления процессом (последовательности действий) если:
- процесс (операция) может быть интерпретирован, как многошаговый процесс выбора управляющих параметров;
- процесс (операция) определен для любого числа шагов и имеет структуру, не зависящую от числа шагов;
- число параметров, характеризующих состояние процесса (операции, системы) на каждом шаге, не зависит от числа шагов;
- процесс (операция) является Марковским, т. е. очередное его состояние зависит только от настоящего состояния и не зависит от того, как процесс пришел в это состояние;
- целевая функция (показатель эффективности) обладает свойством разъединения прошлого и настоящего: является аддитивным или мультипликативным.
Наиболее важным в модели ДП является понятие состояния системы. В общем случае состояние системы 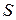 можно отождествить с точкой
можно отождествить с точкой  – мерного пространства
– мерного пространства  . Переходя из состояния в состояние, система
. Переходя из состояния в состояние, система 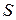 осуществляет переход из одной точки пространства в другую (один шаг), описывая траекторию. Оптимизируя управление состоянием системы между последовательными шагами, удается получить
осуществляет переход из одной точки пространства в другую (один шаг), описывая траекторию. Оптимизируя управление состоянием системы между последовательными шагами, удается получить  оптимальное управление в целом на всем пути (траектории) состояния системы
оптимальное управление в целом на всем пути (траектории) состояния системы 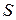 .
.
Пусть рассматриваемая система 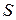 находится в начальном состоянии
находится в начальном состоянии  и под действием управления
и под действием управления  может перейти в конечное состояние
может перейти в конечное состояние  .
.
Замечание. Модели, в которых начальное и конечное состояния определены, называются моделями с фиксированными концами.
Определение. Управление, удовлетворяющее ограничениям, связанными с условиями осуществления процесса, называется допустимым.
Качество любого из допустимых управлений характеризуется значением целевой функции  – показателя качества.
– показателя качества.
Требуется из множества допустимых управлений  найти такое управление
найти такое управление  , при котором показатель качества принимает экстремальное (
, при котором показатель качества принимает экстремальное ( или
или  ) значение
) значение  или
или  .
.
Определение. Управление  называется оптимальным управлением.
называется оптимальным управлением.

Для нахождения оптимального управления  введем следующие предположения:
введем следующие предположения:
1) процесс управления системой 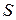 состоит из
состоит из  шагов, на каждом из которых состояние системы определяется совокупностью
шагов, на каждом из которых состояние системы определяется совокупностью  переменных
переменных
 ,
,  ,
,
где  – начальное,
– начальное,  – конечное состояния системы;
– конечное состояния системы;
2) на  -м шаге (
-м шаге (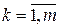 ) управление
) управление  переводит систему из состояния
переводит систему из состояния 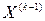 , достигнутого в результате
, достигнутого в результате  -го шага, в состояние
-го шага, в состояние 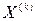 ;
;
3) состояние 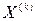 зависит только от состояния
зависит только от состояния 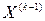 и выбранного управления
и выбранного управления  и не зависит от того, каким было и как осуществлялось управление на предыдущих шагах – условие отсутствия последействия;
и не зависит от того, каким было и как осуществлялось управление на предыдущих шагах – условие отсутствия последействия;
4) если в результате реализации  -го шага значение показателя качества равно
-го шага значение показателя качества равно  , то общее значение показателя качества за
, то общее значение показателя качества за  шагов равно
шагов равно  . Данное выражение есть условие аддитивности целевой функции.
. Данное выражение есть условие аддитивности целевой функции.
Эти предположения позволяют сформулировать принцип оптимальности Беллмана, который лежит в основе методологии нахождения оптимального управления: каково бы ни было начальное состояние и начальное управление, последующее управление должно быть оптимальным по отношению к состоянию, получаемому в результате действия начального управления.
Процесс динамического программирования состоит из двух частей:
- планирование управления на каждом шаге, в результате которого находятся условные оптимальные управления и условные оптимальные выигрыши на каждом шаге, а также оптимальный выигрыш всей операции;
- выбор совокупности управлений на каждом шаге (управления операцией в целом) обеспечивающей найденный максимум (минимум) целевой функции – показателя эффективности проведения операции.
Управление на каждом шаге должно выбираться не отдельно от других шагов, а с учетом всех его последствий в будущем. Управление на данном шаге выбирается таким, чтобы была максимальной сумма выигрышей на всех оставшихся до конца шагах плюс на данном шаге. Исключением из этого правила является последний шаг, который может планироваться без оглядки на будущее. Этот шаг должен планироваться первым и именно таким образом, чтобы он сам (без других шагов) принес наибольшую выгоду.
Поэтому процесс динамического программирования при планировании управления на каждом шаге обычно разворачивается в направлении от последнего шага к первому. Планируя последний m –й шаг нужно сделать разные предположения, чем мог бы закончиться предпоследний m -1–й шаг. Для каждого такого предположения нужно найти условное оптимальное управление и соответствующий ему условный оптимальный выигрыш. Управление и выигрыш называются условными потому, что управление выбирается исходя из условия, что предыдущий шаг закончился именно так. Выигрыш на данном шаге получается при выбранном управлении на этом шаге.
При выборе условного оптимального управления рассматриваются (перебираются) все возможные исходы предыдущего шага и выбирается оптимальное на этом шаге управление. Спланировав m-й шаг при различных условиях окончания m–1-го шага, мы планируем m–1-й шаг при различных условиях окончания m–2-го шага, затем m-2-й шаг при различных условиях окончания m–3-го шага и так далее до первого шага.
Планирование условного оптимального управления на первом шаге сразу же позволяет вычислить оптимальный выигрыш W (U *) всей операции в целом, поскольку условные оптимальные управления за последующие шаги уже найдены.
После того как будут найдены все условные оптимальные управления и условные оптимальные выигрыши за весь «хвост» процесса, можно начать формировать оптимальное управление всей операцией U * (т. е. выбирать совокупности управлений на каждом шаге в направлении от первого шага к последнему шагу ). Под понятием «хвост» процесса подразумеваются все шаги, начиная от данного шага и до последнего шага.
Так как известно, в каком состоянии S 0 была система в начале первого шага, то можно из множества возможных управлений на первом шаге выбрать оптимальное управление u 1*.
В результате применения этого управления u 1* система перейдет из состояния S 0 в новое состояние S 1*. В этом состоянии система находится в начале 2-го шага, поэтому можно из множества возможных управлений на втором шаге выбрать оптимальное управление u 2*. Продолжая подобным образом, мы получаем всю совокупность шаговых управлений U * = (u1*, u2*, …, um*).
Иными словами, если, при управлении системой 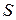 , некоторые управления
, некоторые управления  (и соответствующие им состояния
(и соответствующие им состояния  ) уже выбраны, то необходимым условием нахождения оптимального управления
) уже выбраны, то необходимым условием нахождения оптимального управления  при выборе последующих управлений
при выборе последующих управлений  (и соответствующих им состояний
(и соответствующих им состояний  ) является условие экстремума функции:
) является условие экстремума функции:
 .
.
Получим рекуррентные соотношения Беллмана.
Пусть  –
–  значение показателя качества при переходе из состояния
значение показателя качества при переходе из состояния 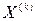 в состояние
в состояние  , тогда, полагая
, тогда, полагая
 ,
,
основное функциональное уравнение, выражающее принцип оптимальности, примет вид  , где
, где 
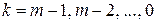 , а
, а  берется по всем управлениям
берется по всем управлениям  , допустимым на шаге
, допустимым на шаге  .
.
Отсюда, при  получим
получим

или  .
.
Данное выражение определяет минимальное (максимальное) значение показателя качества при переходе из состояния  в состояние
в состояние  .
.
Определение. Совокупность управлений 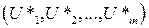 , обеспечивающая экстремальное значение целевой функции, называется оптимальной стратегией управления (ОСУ).
, обеспечивающая экстремальное значение целевой функции, называется оптимальной стратегией управления (ОСУ).
При построении функций  на каждом шаге находятся условные оптимальные управления (УОУ).
на каждом шаге находятся условные оптимальные управления (УОУ).
Определение. Условными оптимальными управлениями называются управления  , равные значениям оптимального управления
, равные значениям оптимального управления  шага при всевозможных состояниях системы на предыдущем
шага при всевозможных состояниях системы на предыдущем  -м шаге.
-м шаге.
Приведем алгоритм построения стратегии управления.
I ход (обратный). В соответствии с принципом оптимальности найти условные оптимальные управления (УОУ)  на каждом шаге, переходя от последнего шага к первому, для чего следует произвести:
на каждом шаге, переходя от последнего шага к первому, для чего следует произвести:
1. Условную оптимизацию последнего  -го шага.
-го шага.
Для этого необходимо вычислить значения показателя качества каждого из переходов в конечное состояние  , рассматривая все состояния системы
, рассматривая все состояния системы 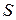 , из которых этот переход можно осуществить за один последний шаг
, из которых этот переход можно осуществить за один последний шаг
 .
.
2. Условную оптимизацию  -го шага для любых состояний системы, используя полученные за предыдущий шаг значения
-го шага для любых состояний системы, используя полученные за предыдущий шаг значения 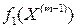
 .
.
3. Условную оптимизацию  -го шага,
-го шага, 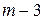 -го шага и т. д. до второго шага включительно.
-го шага и т. д. до второго шага включительно.
4. Указать с помощью рекуррентных соотношений условное оптимальное управление.

5 Поскольку рассматривается модель с фиксированными концами, то на первом шаге варьировать состояния не нужно, найденное условное оптимальное управление для начального состояния  совпадает с искомым оптимальным управлением на первом шаге.
совпадает с искомым оптимальным управлением на первом шаге.
II ход (прямой). «Восстановить» оптимальную стратегию управления по условным оптимальным стратегиям, начиная с первого шага.
Замечание. Этот алгоритм используется также и при реализации моделей с незакрепленными концами, в которых начальное и конечное состояния не единственны, а выбираются из множества начальных и множества конечных состояний.
В моделях с незакрепленными концами при выполнении условной оптимизации последнего шага вычисляются значения показателя качества переходов в любое из конечных состояний  , среди которых и находится наибольшее (наименьшее) значение для каждого из состояний
, среди которых и находится наибольшее (наименьшее) значение для каждого из состояний  .
.
При выполнении п. 5 условная оптимизация первого шага выполняется для любого из начальных состояний, что позволяет выделить то начальное состояние, у которого значение целевой функции максимально (минимально).
“Восстановление” оптимальной стратегии управления в прямом ходе производится так же, как и для задач с фиксированными концами. Если наибольшего (наименьшего) значения целевой функции достигают сразу несколько начальных состояний, то ОСУ не единственна.
Приведем несколько задач, в которых управления состоянием системы могут быть описаны моделями ДП.
Следует заметить, что значение W (U *) стало известно сразу после определения условных оптимальных управлений, т. е. еще до выбора u1*. Поэтому при формировании оптимального управления всей операцией U* задача состоит в том, чтобы выбирать такие ui*, которые позволили бы сформировать управление всей операцией U* с уже известным значением W(U*).
В основе метода динамического программирования лежит следующий принцип оптимальности:
На каждом этапе оптимальная стратегия определяется независимо от стратегий, примененных на предыдущих этапах. Оптимальная стратегия обладает тем свойством, что каковы бы ни были первоначальное состояние системы и первоначальный выбор, последующие выборы должны составлять оптимальную программу относительно состояния, полученного в результате первоначального выбора.
Последовательность действий при формулировке и решении задач динамического программирования
При формулировке задачи динамического программирования целесообразно придерживаться следующей последовательности действий:
- определить, что является шагом процесса, а если процесс непрерывный, то произвести искусственное разбиение его на шаги;
- определить параметры, характеризующие вектор состояний процесса (состояний объекта управления), и пределы их изменений;
- определить параметры управления (вектор управления), и пределы их изменений;
- определить функциональную зависимость состояний процесса от параметров управления (уравнение процесса), указывающую на правило перевода процесса из состояния в состояние в зависимости от принятого (примененного) управления;
- с учетом выбранной целевой функции (показателя эффективности) составить функциональное уравнение, математически выражающее принцип оптимальности.
Специфика каждой конкретной задачи динамического программирования сказывается на виде функционального уравнения, виде целевой функции, числе и виде параметров состояния процесса и управляющих параметров.
В связи с этим не существует единого алгоритма, позволяющего решить любую задачу, сформулированную, как задачу динамического программирования. Хотя каждая задача решается специфическим образом, для всех задач динамического программирования имеется и общее, которое заключается в решении задач в два этапа:
- На первом этапе с помощью функционального уравнения последовательно находятся значения целевой функции (показателя эффективности) для всех значений параметров состояния и управляющих параметров на каждом шаге начиная с последнего до первого шага;
- На втором этапе, используя полученные значения целевой функции, последовательно начиная с первого до последнего шага, находятся соответствующие максимуму (минимуму) значения целевой функции значения управляющих параметров и значения параметров состояния на следующем шаге. Полученная совокупность значений управляющих переменных и есть стратегия, обращающая целевую функцию (показатель эффективности) в максимум (минимум).
Не нашли, что искали? Воспользуйтесь поиском: