
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задачи, решаемые методами динамического программирования
В задачах динамического программирования вычисления выполняются рекуррентно в том смысле, что оптимальное решение одной подзадачи используется в качестве исходных данных для следующей подзадачи. Решив последнюю подзадачу, мы получим оптимальное решение исходной задачи. Способ выполнения рекуррентных вычислений зависит от того, как выполняется декомпозиция исходной задачи. В частности, подзадачи обычно связаны между собой некоторыми общими ограничениями. Если осуществляется переход от одной подзадачи к другой, то должны учитываться эти ограничения.
В ряде задач динамического программирования нет разницы между началом и концом процесса, как в приведенном ниже примере. В этом примере планирование управления на каждом шаге производится в направлении от первого шага к последнему шагу. А формирование оптимального управления всей операцией U * – в направлении от последнего шага к первому. Такое становится возможным, когда значение целевой функции не зависит от направления движения. В данном примере кратчайший маршрут между первым и седьмым городом не зависит от направления, в котором мы начнем путешествие: из первого города или из последнего.
Выбор кратчайшего пути на сети
Предположим, необходимо выбрать кратчайший путь между двумя городами. Сеть дорог, показанная на рис, представляет возможные маршруты между исходным городом, находящимся в узле (вершине графа) 1, и конечным пунктом, который находится в узле 7. Маршруты проходят через промежуточные города, обозначенные на сети узлами с номерами 2-6. Расстояния между городами в милях проставлены дугами между вершинами графа (узлами).
|

Мы можем решить эту задачу посредством полного перебора всех маршрутов между узлами 1 и 7 (имеется пять таких маршрутов). Однако в большой сети полный перебор является неэффективным с вычислительной точки зрения.
Чтобы решить эту задачу с помощью методов динамического программирования, сначала разделим ее на шаги. Вертикальные пунктирные линии на втором рисунке очерчивают три шага задачи. Далее выполняются вычисления для каждого этапа в отдельности.
Общая задача состоит в вычислении кратчайших (постепенно накапливаемых) расстояний ко всем вершинам шага с последующим использованием этих расстояний в качестве исходных данных для следующего шага. Рассматривая узлы, относящиеся к первому шагу, замечаем, что каждый из узлов 2, 3 и 4 связан с начальным узлом 1 единственной дугой (рис.). Следовательно, для первого шага имеем следующее.

|
Шаг 1. Итоговые результаты.
Кратчайший путь из узла 1 к узлу 2 равен 7 миль,
Кратчайший путь из узла 1 к узлу 3 равен 8 миль,
Кратчайший путь из узла 1 к узлу 4 равен 5 миль.
Далее переходим ко второму шагу для вычисления кратчайших (накопленных) расстояний к узлам 5 и 6. Рассматривая узел 5 первым, из второго рисунка, замечаем, что есть три возможных маршрута, по которым можно достичь узла 5, а именно (2, 5), (3, 5) и (4,5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3, и 4 определяет кратчайшее (накопленное) расстояние к узлу 5 следующим образом.
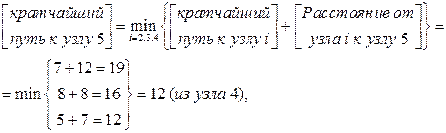
Аналогично для узла 6 имеем следующее.
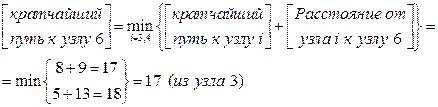
Шаг 2. Итоговые результаты.
Кратчайший путь из узла 1 к узлу 5 равен 12 миль,
Кратчайший путь из узла 1 к узлу 6 равен 17 миль.
Шаг 3. Последним шагом является третий шаг. Конечный узел 7 можно достигнуть как из узла 5, так и 6. Используя итоговые результаты шага 2 и расстояния от узлов 5 и 6 к узлу 7, получаем следующее.
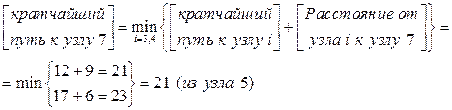
Шаг З. Итоговые результаты.
Кратчайший путь к узлу 7 равен 21 миле.
Приведенные вычисления показывают, что кратчайшее расстояние между узлами 1 и 7 равно 21 миле. Города, через которые проходит кратчайший маршрут, определяются следующим образом. Из итоговых результатов третьего шага следует, что узел 7 связывается с узлом 5. Далее из итоговых результатов второго шага следует, что узел 4 связывается с узлом 5. Наконец, из итоговых результатов первого шага следует, что узел 4 связывается с узлом 1. Следовательно, оптимальным маршрутом является последовательность 1-4-5-7,
Теперь покажем, как рекуррентные вычисления динамического программирования можно выразить математически.
Пусть i-номер шага. Рассмотрим «прямой» маршрут от начальной вершины к конечной.
Пусть fi(xi) — кратчайшее расстояние от вершины х 0 до вершины хi на этапе i, d (хi- 1, хi) — расстояние от узла хi- 1 до узла хi. Тогда fi вычисляется из fi -1 с помощью следующего рекуррентного уравнения.
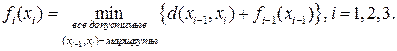
При i= 1 полагаем f 0(x 0)= 0. Это уравнение показывает, что кратчайшие расстояния fi (xi)на этапе i должны быть выражены как функции следующего узла хi. В терминологии динамического программирования хi именуется состоянием системы на этапе i.
Для обратного маршрута используется следующее рекуррентное уравнение.
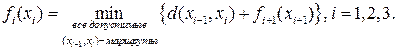
В действительности состояние системы на этапе i – это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах.
Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.
Определение состояния системы приводит к следующему унифицированному положению.
Применение принципа оптимальности демонстрируется вычислениями из рассмотренного примера. Например, на этапе 3 мы используем кратчайшие пути к узлам 5 и 6 и не интересуемся, как эти узлы были достигнуты из узла 1.
Пример 2.
Пусть требуется продолжить трубопровод между пунктами А, В так, чтобы затраты были минимальными.
Разобьем расстояние на шаги, отрезки и будем считать, что на каждом шаге возможно движение только на север или на восток. Тогда путь представляет собой ломаную линию. Разделим на три части каждое из направлений: на восток и на север.
Известны затраты, потребные на сооружение каждого участка.
| 12 12 | ||
| 15 10 | ||
| 10 12 |
Решение:
Разобьем расстояние от А до В в восточном направлении и в северном направлении на 3 части. Найдем условную оптимизацию последнего шага. В данную точку можно попасть двумя путями с расстояниями 10 (точка В1) и 14 (точка В2). В узлах напишем стоимость пути. Стрелкой укажем минимальный путь.

Рассмотрим предпоследний шаг. Для точки В3 условное направление по оси Х и для точки В5 – по оси У. Для точки В4 выберем минимальное значение, что соответствует оптимальному управлению, 

Продолжая дальнейшее движение, получим
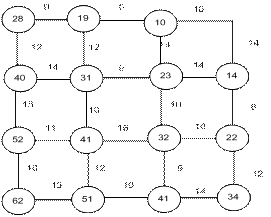
Минимальные затраты составят 62 млн. руб. Ему соответствует решение (с, в, с, в, с, в). Следует отметить, что для данного примера оптимальное решение совпадет, если не использовать метод динамического программирования, а находить оптимальное решение на каждом шаге, то получим решение
Не нашли, что искали? Воспользуйтесь поиском: