
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача распределения ресурсов
Пусть имеется некоторое количество экономических ресурсов. Под термином ресурсы подразумеваются люди, деньги, машины, материалы для технологических процессов, вода для сельскохозяйственных и промышленных целей, топливо и т.д. Эти ресурсы потребляются различными способами, в результате чего получают некоторой доход, размер которого зависит от употребленного количества ресурсов и от выбранного процесса распределения.
Задача заключается в распределении ресурсов таким образом, чтобы максимизировать общий доход при следующих условиях: доходы, полученные от различных процессов, измеряются общей единицей; доход, полученный от рассматриваемого процесса, не зависит от количества ресурсов, выделенных для других процессов; общий доход получается как сумма доходов полученных от отдельных процессов.
Математическая формулировка задачи следующая. Пусть имеется N различных процессов (i = 1, 2,..., N), каждому из которых соответствует функция полезности – целевая функция (доход) Q i, зависящая от количества выделенных ресурсов u ι. Общий доход определяется аддитивной функцией
 .
.
На количество ресурсов наложены ограничения, что общее их количество не должно превышать заданного, 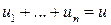 , где u ι ≥ 0.
, где u ι ≥ 0.
Конкретным примером рассматриваемой задачи является процесс распределения капиталовложений между предприятиями.
Задача о загрузке
Необходимо загрузить корабль грузом, составленным из отдельных предметов различного типа, имеющих различные массу и стоимость. Задача состоит в загрузке судна ограниченной грузоподъемности грузом наибольшей стоимости.
Данная задача – это задача о рациональной загрузке судна (самолета, автомашины), которое имеет ограничения по грузоподъемности или объему. Каждый помещенный груз приносит прибыль. Задача загрузки состоит в определении загрузки, приносящей наибольшую суммарную прибыль.
К таким задачам относится также задача о снаряжении, где пилот самолета выбирает вариант подвески и задача о рюкзаке, где турист должен выбрать наиболее ценные товары
Математическая модель задачи имеет вид:

Варианты решения задачи определяются следующим образом.
Введем обозначения:
mi – количество предметов i-го типа, загружаемых в самолет (i=1, 2, 3);
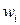 - вес каждого предмета;
- вес каждого предмета;
 - общий вес (грузоподъемность самолета);
- общий вес (грузоподъемность самолета);
 – суммарная стоимость предметов i -го типа (x), загруженных в самолет – частный показатель эффективности;
– суммарная стоимость предметов i -го типа (x), загруженных в самолет – частный показатель эффективности;
 – общая стоимость груза, загруженного в самолет – общий показатель эффективности;
– общая стоимость груза, загруженного в самолет – общий показатель эффективности;
Задачу можно решить симплекс-методом, но целочисленные решения не гарантируются.
f i,3(x) – максимальная стоимость груза при оптимальной загрузке в самолет предметов с i-го по 3-й (последний).
Этап в нашей задаче – загрузка в самолет предметов одного типа.
1. Допустим, что на 1-м этапе мы загружаем в самолет x -предметов 1-го типа, тогда для предметов 2-го и 3-го типа останется в самолете (w-w 1* m) тонн. В этом случае стоимость груза в самолете будет определяться как сумма
c 1* m 1+ f 2 (w - w 1* m).
По определению:
|
Получили рекуррентное соотношение, которое может быть записано параметрически, но не определено численно, т.к. в правой части есть неопределенный элемент f 2,3.
2. Второе допущение: пусть в самолет мы не загрузили предметы 1-го типа, а предметов второго типа мы загрузили x. Тогда для предметов 3-го типа осталось в самолете (w-w2*m) тонн. Тогда по аналогии с п.1 получаем:
|
Второе рекуррентное соотношение тоже не может быть определено численно.
3. Пусть в самолет не загружаются предметы 1-го и 2-го типа, а загружают m предметов 3-го типа. Тогда:
|
Данная неизвестная может быть рассчитана численно (нет необходимости учитывать последние этапы – он и есть последний).
Определив f 3,3(m), подставляем ее значение в предыдущее выражение и определяем f 2,3(m), а затем f 1,3(m).
Рассчитав значения f i,3(m) можно осуществить выбор управляющих воздействий на каждом этапе.
Этапы решения задачи:
1. Параметрической определение рекуррентных соотношений.
2. Численный расчет функциональных уравнений.
3. Составление оптимальной программы.
Пример. Самолет загружается предметами N различных типов. Каждый предмет типа i имеет вес wi и стоимость ci (i=1, 2, 3). Максимальная грузоподъемность самолета равна W. Требуется определить максимальную стоимость груза, вес которого не должен превышать максимальную грузоподъемность самолета. Предположим, что W =4 т и всего имеется три типа предметов (N =3), численные сведения о которых приведены в таблице:
| i | wi | ci |
Оптимальное решение данной задачи легко найти путем полного перебора вариантов. На практике чаще всего встречаются задачи, в которых количество типов предметов достаточно велико. Поиск решения таких задач методом полного перебора сопряжен со значительными сложностями:
1. В задачах средней и большой размерности объем необходимых вычислений становится чрезвычайно большим.
2. Отсутствует априорная информация о решениях, которые не являются допустимыми, что снижает эффективность вычислительной схемы полного перебора.
3. Информация, полученная в результате анализа некоторых комбинаций проектов, в дальнейшем не используется для выявления и исключения неоптимальных комбинаций.
Этап 3.
Пусть  -число предметов
-число предметов  -го типа,
-го типа,  - суммарный вес предметов, решение о погрузке которых принято на
- суммарный вес предметов, решение о погрузке которых принято на  -м этапе.
-м этапе.
Точный вес, который может быть загружен на третьем этапе при загрузке третьего типа предметов, заранее неизвестен. Состояния  являются крайними случаями, когда предметы третьего наименования полностью не загружаются или в самолет загружаются только предметы третьего наименования. Так как вес предметов третьего типа равен 1 тонне, то в самолет загружается 0,1, 2, 3 или 4 предмета третьего типа.
являются крайними случаями, когда предметы третьего наименования полностью не загружаются или в самолет загружаются только предметы третьего наименования. Так как вес предметов третьего типа равен 1 тонне, то в самолет загружается 0,1, 2, 3 или 4 предмета третьего типа.
Решение 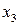 будет допустимым только, если
будет допустимым только, если  . Следовательно, все недопустимые альтернативы будут исключены. Следующее соотношение будет основным для третьего этапа.
. Следовательно, все недопустимые альтернативы будут исключены. Следующее соотношение будет основным для третьего этапа.
 .
.
Построим таблицу, в которой будут содержаться результаты частных шагов решения для третьего этапа.
| m 3 | |||||||
| X 3 | f 3(x3) | m3* | |||||
На втором этапе функциональное уравнение будет иметь вид:
 .
.
Таблица с содержимым результатов частных шагов решения имеет вид
| m 2 | m 2* | |||
| X 2 | f 2(x2) | |||
| 0+0 | ||||
| 0+14 | ||||
| 0+28 | ||||
| 0+42 | 47+0=47 | |||
| 0+56 | 47+14=61 |
Этап 1

| m 1 | f 1(x1) | m 1* | |||
| X 1 | |||||
| 0+0 | |||||
| 0+14 | |||||
| 0+28 | 31+0=31 | ||||
| 0+47 | 31+14=45 | ||||
| 0+61 | 31+28=59 | 62+0=62 |
Оптимальное решение определяется следующим образом. Из условия, что вес равен 4 тонн, оптимальное решение равно 62 000.
Не нашли, что искали? Воспользуйтесь поиском: