
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчеты на прочность и жесткость с учетом сил инерции
Напомним принцип Даламбера.
Если в любой момент времени к каждой точке системы, кроме фактически действующих на нее внешних и внутренних сил, приложить силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять все уравнения статики.
Силой инерции называют векторную величину, равную по модулю произведению массы на ускорение и направленную противоположно этому ускорению. Во многих случаях ускорения точек деформируемого тела могут быть найдены из анализа условий его работы. При известных ускорениях задача расчета на прочность и жесткость приводится к случаю статического действия нагрузок путем использования принципа Даламбера. Поясним алгоритм решения задачи на примере.
Пусть груз весом Q, подвешенный на тросе площадью поперечного сечения F, поднимается с помощью лебедки с ускорением  . Весом троса пренебрегаем. Требуется определить напряжения в тросе и его удлинение (рис. 19.1).
. Весом троса пренебрегаем. Требуется определить напряжения в тросе и его удлинение (рис. 19.1).
| а) |
| l |

|
| z |
| z |
| Nz |
| Q |
| z |

|
| б) |
Рис. 19.1. Определение напряжений в тросе при подъеме груза
Выделим участок троса длиной z (рис.19.1б). Если бы груз поднимался с постоянной скоростью (без ускорения), то на рассматриваемый участок троса действовала бы сила веса груза  и внутренняя продольная сила Nz. При подъеме с ускорением
и внутренняя продольная сила Nz. При подъеме с ускорением  в соответствии с принципом Даламбера прикладываем дополнительную внешнюю силу
в соответствии с принципом Даламбера прикладываем дополнительную внешнюю силу  (сила инерции груза). Здесь g – ускорение свободного падения. Таким образом, динамическую задачу удалось свести к статической. Тогда можем записать условие равновесия по оси z -
(сила инерции груза). Здесь g – ускорение свободного падения. Таким образом, динамическую задачу удалось свести к статической. Тогда можем записать условие равновесия по оси z -  и найти по методу сечений нормальную силу
и найти по методу сечений нормальную силу  :
:
 .
.
Напряжения в сечении z будут равны:
 (19.1)
(19.1)
Величина  представляет собой напряжения в тросе при статическом приложении нагрузки, а
представляет собой напряжения в тросе при статическом приложении нагрузки, а  - динамический коэффициент. Если ускорение будет направлено вниз (начальный период опускания груза), то в выражении для динамического коэффициента изменится знак второго слагаемого и при
- динамический коэффициент. Если ускорение будет направлено вниз (начальный период опускания груза), то в выражении для динамического коэффициента изменится знак второго слагаемого и при  напряжения в тросе будут отсутствовать.
напряжения в тросе будут отсутствовать.
Перемещение произвольного сечения при  будет равно удлинению верхней части стержня (от заделки в шкив до текущего сечения)
будет равно удлинению верхней части стержня (от заделки в шкив до текущего сечения)
 .
.
Координата  изменяется в пределах
изменяется в пределах  Наибольшее перемещение наблюдается в точке крепления груза к тросу и численно равно его удлинению:
Наибольшее перемещение наблюдается в точке крепления груза к тросу и численно равно его удлинению:
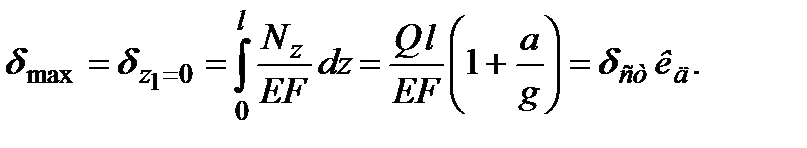 (19.2)
(19.2)
Не нашли, что искали? Воспользуйтесь поиском: