
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчеты на прочность и жесткость при ударном действии нагрузок
Под ударной будем понимать всякую быстро изменяющуюся нагрузку. Таким образом, кроме удара в обычном смысле слова, к ударной нагрузке будем относить, например, случай нагружения упругой системы при ее внезапном торможении. Так, при свободном падении тела с высоты 5 м его скорость в момент соударения с землей составит порядка 10м/с, соответствующей будет и скорость нагружения тела.
Определение перемещений, деформаций и напряжений, возникающих в конструкции при ударе, осложняется рядом трудно учитываемых факторов. Например, напряженное состояние в зоне контакта соударяющихся тел резко отличается от напряженного состояния в других точках тела. При этом могут возникать значительные местные пластические деформации и местный нагрев. При переходе от перемещений к деформациям и напряжениям возникают дополнительные трудности, связанные с установлением связи между напряжениями и деформациями при больших скоростях нагружения.
При технических расчетах влиянием большинства выше перечисленных факторов пренебрегают и задача сводится к анализу движения ударяющего тела и упругой системы при их взаимодействии.
Пусть тело массой m ударяет по упругой системе, жесткость которой с, а масса самой упругой системы пренебрежимо мала по сравнению с массой ударяющего тела (рис. 19.5). Предположим, что в момент удара тело имеет скорость V, а после удара оно не отделяется от упругой системы. Таким образом, задача сведена к анализу совместному движению тела и упругой системы после контакта. В результате решения соответствующего дифференциального уравнения получим уравнение движения, из которого можно определить максимальные перемещения системы, а затем и напряжения, как это делалось при рассмотрении колебаний. Однако максимальные перемещения системы можно найти и, не решая дифференциальные уравнения, из энергетических соображений.
| δст |
|
| m |
| V |
| c |
Рис. 19.5. Удар тела массой m по упругой системе
Предположим, что энергия, потерянная ударяющим телом, полностью переходит в потенциальную энергию деформации упругой системы U. Изменение энергии ударяющего тела в момент, соответствующий наибольшей деформации  упругой системы при вертикальном ударе, равно (когда скорость ударяющего тела становится равной нулю)
упругой системы при вертикальном ударе, равно (когда скорость ударяющего тела становится равной нулю)
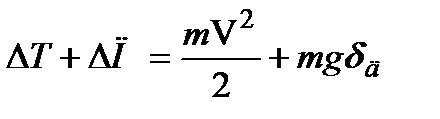 (19.19)
(19.19)
где 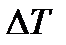 - изменение кинетической энергии;
- изменение кинетической энергии;
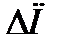 - изменение потенциальной энергии при перемещении
- изменение потенциальной энергии при перемещении 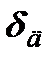 .
.
Определим потенциальную энергию системы в момент наибольшей упругой деформации 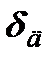 . Действие ударяющего тела на упругую систему заменим статически прикладываемой силой
. Действие ударяющего тела на упругую систему заменим статически прикладываемой силой  , вызывающей перемещение
, вызывающей перемещение 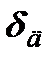 в точке приложения этой силы. Очевидно:
в точке приложения этой силы. Очевидно:
 , (19.20)
, (19.20)
здесь  - жесткость упругой системы при динамическом нагружении предполагается равной жесткости системы при статическом нагружении.
- жесткость упругой системы при динамическом нагружении предполагается равной жесткости системы при статическом нагружении.
Приравнивая выражения (19.19) и (19.20), получим
 (19.21)
(19.21)
Решая полученное квадратное уравнение, получим
 (19.22)
(19.22)
где  - коэффициент динамичности. Как следует из проведенного анализа, при вертикальном ударе он равен
- коэффициент динамичности. Как следует из проведенного анализа, при вертикальном ударе он равен
 (19.23)
(19.23)
где V – скорость ударяющего тела в момент контакта с упругой системой;
g – ускорение свободного падения;
 - перемещение в точке удара при действии статической силы, равной весу ударяющего тела.
- перемещение в точке удара при действии статической силы, равной весу ударяющего тела.
Если известна не скорость ударяющего тела, высота свободного падения Н  , то выражение для коэффициента динамичности примет вид:
, то выражение для коэффициента динамичности примет вид:
 (19.24)
(19.24)
При горизонтальном ударе полученные ранее соотношения баланса энергии приобретают вид:
 (19.25)
(19.25)
Отсюда коэффициент динамичности при горизонтальном ударе определяется соотношением:
 (19.26)
(19.26)
Рассмотрим случай внезапного торможения системы, состоящей из упругой связи С и груза Р массой m, движущегося равномерно со скоростью V. Массой упругой системы пренебрегаем. Перемещение точки подвески груза по сравнению с ненагруженным состоянием равно  (рис. 19.6)
(рис. 19.6)
| δст |
| δд |
| m |
| V |
| c |
| Р |
| Рд |
| Рст |
| δст |
| δд |
| δ |
Рис. 19.6. Внезапное торможение упругой системы
При внезапном прекращении движения приращение потенциальной энергии деформации 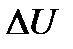 в момент, соответствующий наибольшему перемещению
в момент, соответствующий наибольшему перемещению  точки подвески груза, численно равно изменению кинетической и потенциальной энергии груза массой m, т.е.
точки подвески груза, численно равно изменению кинетической и потенциальной энергии груза массой m, т.е.
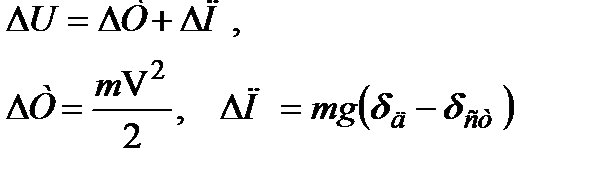 . (19.27)
. (19.27)
С другой стороны, изменение потенциальной энергии самой упругой системы 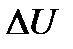 можно получить из соотношения:
можно получить из соотношения:
 (19.28)
(19.28)
Приравнивая выражения (19.27) и (19.28), получим
 . (19.29)
. (19.29)
После несложных преобразований получим:
 (19.30)
(19.30)
Решая полученное уравнение относительно  , имеем
, имеем
 (19.31)
(19.31)
где коэффициент динамичности равен
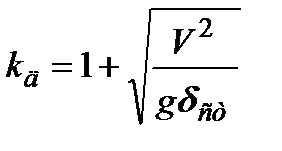 . (19.32)
. (19.32)
Таким образом, на примере простейших упругих систем мы показали, что при ударном нагружении максимальные перемещение следует определять соотношением
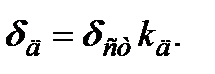 (19.33)
(19.33)
Во всех рассмотренных случаях  - это перемещение рассматриваемой точки конструкции при статическом приложении силы, равной весу ударяющего тела, а
- это перемещение рассматриваемой точки конструкции при статическом приложении силы, равной весу ударяющего тела, а  - коэффициент динамичности, который определяется особенностями взаимодействия тел при ударе и в рассмотренных выше случаях вычисляется по формулам (19.23), (19.24), (19.26) и (19.32).
- коэффициент динамичности, который определяется особенностями взаимодействия тел при ударе и в рассмотренных выше случаях вычисляется по формулам (19.23), (19.24), (19.26) и (19.32).
Предполагая, что напряжения прямо пропорциональны деформациям, для динамических напряжений при ударе имеем
 , (19.34)
, (19.34)
где  - напряжения в рассматриваемой точке при статическом приложении силы, равной весу ударяющего тела.
- напряжения в рассматриваемой точке при статическом приложении силы, равной весу ударяющего тела.
Рассмотренный энергетический метод расчета на прочность и жесткость при ударном действии нагрузок не учитывает массу самой упругой системы. Это приводит к завышению значений динамических перемещений, однако, динамические напряжения могут быть как больше, так и меньше своих истинных значений. Изложенная методика дает удовлетворительные результаты, если отношение веса ударяющего тела к весу упругой системы не менее 5…10, а скорость ударяющего тела значительно меньше скорости распространения возмущений в теле.
При оценке прочности максимальное динамическое напряжение сопоставляют с допускаемым напряжением, при определении которого коэффициент запаса прочности повышают, например, от 1,5…1,6 при статическом нагружении до 2,0 при динамическом нагружении.
Не нашли, что искали? Воспользуйтесь поиском: