
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчеты на прочность и жесткость при колебаниях
Расчеты на прочность и жесткость при колебаниях основываются на исследовании движения механических систем методами теоретической механики и математической физики. Напомним некоторые основные положения теории колебаний систем с одной степенью свободы.
Положение некоторой характерной точки системы во времени задается функцией  , которая называется законом колебаний данной точки. Важной особенностью данной функции, описывающей колебательный процесс, является наличие большого числа экстремумов. Речь может идти о линейных или угловых колебаниях, а также о колебаниях других параметров, зависящих от закона колебаний тела: скорости, деформации, напряжений и др.
, которая называется законом колебаний данной точки. Важной особенностью данной функции, описывающей колебательный процесс, является наличие большого числа экстремумов. Речь может идти о линейных или угловых колебаниях, а также о колебаниях других параметров, зависящих от закона колебаний тела: скорости, деформации, напряжений и др.
Простейшими являются гармонические колебания:
 , (19.3)
, (19.3)
где  - амплитуда колебаний;
- амплитуда колебаний;
 - круговая частота колебаний [рад/с];
- круговая частота колебаний [рад/с];
φ – фаза колебаний [рад].
В теории колебаний широко используются производные величины, описывающие колебательный процесс:
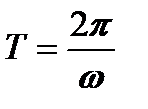 - период колебаний [с];
- период колебаний [с];
 - частота колебаний [1/с = Гц].
- частота колебаний [1/с = Гц].
Движение упругой системы, выведенной из положения равновесия, а затем освобожденной от внешнего воздействия, вызвавшего отклонение от положения равновесия, называют свободными колебаниями. Движение упругой системы под действием переменных внешних нагрузок называют вынужденными колебаниями. Закон колебаний механической системы зависит от числа степеней свободы – числа независимых (обобщенных) координат, определяющих положение всех точек системы в любой момент времени. Если движение тела в целом может быть описано одним уравнением движения характерной точки, то говорят что это система с одной степенью свободы (рис. 19.2).
Массой упругого элемента системы в этом случае пренебрегают, а его жесткость обозначим С. Жесткость упругого элемента численно равна силе Р, которая вызывает перемещение системы, равное единице, т.е.
 . (19.4)
. (19.4)
Положение массы m будем определять относительно положения статического равновесия. Тогда уравнение движения (закон колебаний) запишем в виде:

Решение полученного уравнения имеет вид
 . (19.5)
. (19.5)
| x |

|
| m |
| x |

|
| c |
Рис. 19.2. Собственные колебания системы с одной степенью свободы
Учитывая введенные обозначения, можно определить круговую частоту колебаний
 . (19.6)
. (19.6)
В формуле (19.6)  - перемещение в направлении движения точки сосредоточения массы m под действием силы, равной весу этой массы. Формула (19.6) позволяет экспериментально определить собственную частоту колебаний упругой системы в ряде случаев.
- перемещение в направлении движения точки сосредоточения массы m под действием силы, равной весу этой массы. Формула (19.6) позволяет экспериментально определить собственную частоту колебаний упругой системы в ряде случаев.
На рис. 19.3 показаны некоторые механические системы, которые в первом приближении могут приводиться к системе с одной степенью свободы.
Статические перемещения в этих случаях определяются так:
- рис. 19.3а  ;
;
- рис. 19.3б  ;
;
- рис. 19.3в  .
.
| l |
| m |
| m |
| c2 |
| m |
| a) |
| c1 |
| c2 |

|
| б) |
| c1 |
| в) |
Рис. 19.3. Перемещения в системах с одной степенью свободы
При наличии в системе сил, препятствующих движению (сил демпфирования), их необходимо учитывать при составлении уравнений колебаний. Наиболее простое и в тоже время практически важное решение получается в случае, когда демпфирующая сила пропорциональна скорости движения тела и направлена в сторону противоположную движению (существует термин вязкое сопротивление). Уравнения колебаний примут вид:

Общее решение данного уравнения при силах демпфирования намного меньших сил инерции ( ) находят в виде:
) находят в виде:
 (19.7)
(19.7)
где  . При этом колебания являются затухающими, т.к. амплитуда колебаний
. При этом колебания являются затухающими, т.к. амплитуда колебаний  со временем уменьшается.
со временем уменьшается.
Рассмотрим вынужденные колебания системы с одной степень свободы с учетом демпфирования, которые вызываются периодической силой  , где
, где  - частота вынужденных колебаний, Р0 – амплитуда возбуждающей силы. Уравнения колебаний принято записывать в виде:
- частота вынужденных колебаний, Р0 – амплитуда возбуждающей силы. Уравнения колебаний принято записывать в виде:
 (19.8)
(19.8)
Общее решение дифференциального (19.8) состоит из решения соответствующего однородного уравнения и частного решения общего уравнения. Решение соответствующего однородного уравнения имеет вид (19.7). Частное решение общего уравнения представим в виде:
 ,
,
где  . (19.9)
. (19.9)
В числителе данного выражения имеем  , тогда амплитуда вынужденных колебаний системы с одной степенью свободы (19.9) примет вид:
, тогда амплитуда вынужденных колебаний системы с одной степенью свободы (19.9) примет вид:
 . (19.10)
. (19.10)
Общее решение уравнения (19.8) примет вид
 . (19.11)
. (19.11)
Анализ выражения (19.11) показывает, что фактически вынужденные колебания системы с одной степенью свободы являются наложением двух движений: свободных колебаний с частотой ω1, причем эти колебаний затухают во времени; вынужденных колебаний с частотой Ω и амплитудой  , которые происходят все время приложения возбуждающей силы к системе.
, которые происходят все время приложения возбуждающей силы к системе.
Амплитуда вынужденных колебаний системы  определяется значением динамического коэффициента β, т.е.:
определяется значением динамического коэффициента β, т.е.:
 . (19.12)
. (19.12)
| β |
| 0,5 |
| 1,0 |
| 1,5 |
| 2,0 |
| 1 |
| Ω/ω |
| 2n/ω=0 |
| 2n/ω=0,3 |
| 2n/ω=0,5 |
Рис.19.4. График изменения динамического коэффициента
На рис. 19.4 приведены графики изменения коэффициента β от отношения частот Ω/ω и параметра 2n/ω, который характеризует диссипативные свойства системы. Видно, при Ω/ω<0,5 и Ω/ω>2 параметр 2n/ω мало влияет на динамический коэффициент. При отсутствии сил демпфирования (n=0) имеем
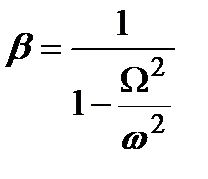 . (19.13)
. (19.13)
Если силы демпфирования в системе малы, то при совпадении частот возбуждающей силы и собственных колебаний наблюдается резкое увеличение амплитуд колебаний – резонанс.
Приведенные результаты анализа колебаний системы с одной степенью свободы показывают, что амплитуда при установившихся вынужденных колебаниях упругой системы может быть определена по формуле
 . (19.14)
. (19.14)
где  - перемещение точек системы при статическом приложении максимальной возбуждающей силы Р0 (ее амплитудное значение), а коэффициент β – это динамический коэффициент, определяемый по формулам (19.12) и (19.13). Если для конкретного случая нагружения выполняется закон Гука, то можно предположить, что напряжения определяются соотношением:
- перемещение точек системы при статическом приложении максимальной возбуждающей силы Р0 (ее амплитудное значение), а коэффициент β – это динамический коэффициент, определяемый по формулам (19.12) и (19.13). Если для конкретного случая нагружения выполняется закон Гука, то можно предположить, что напряжения определяются соотношением:
 . (19.15)
. (19.15)
Если кроме возбуждающей силы на конструкцию действует сила, не изменяющаяся во времени, например, сила тяжести Q, то максимальное перемещение и расчетное напряжение следует определять по формулам:
 ; (19.16)
; (19.16)
 , (19.17)
, (19.17)
где 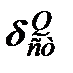 ,
,  - перемещение и напряжение в рассматриваемой точке при действии силы, не изменяющейся во времени.
- перемещение и напряжение в рассматриваемой точке при действии силы, не изменяющейся во времени.
Во многих случаях определить максимальную возбуждающую силу Р0 достаточно сложно. В этих случаях для обеспечения прочности вводят требование:
 (19.18)
(19.18)
Если частота возбуждающей силы Ω известна, то соблюдение неравенства (19.18) обеспечивают соответствующим выбором геометрических характеристик упругой системы (размеров и формы сечений, длины, материала и др.), т.е. путем изменения собственных частот колебаний системы. Здесь следует учесть, что при достаточно «быстром» переходе через резонансную частоту в упругой системе не успевают установиться опасные значения амплитуд вынужденных колебаний. Кроме того, данный подход справедлив для систем с одной степенью свободы, системы с распределенными параметрами имеют бесконечное множество собственных частот колебаний и подлежат более сложному динамическому анализу.
Не нашли, что искали? Воспользуйтесь поиском: