Инерциалды санақ жүйесі

Инерция (лат. іnertіa – әрекетсіздік), материялық денелердің механикадағы Ньютонның 1-және 2-заңдарында көрініс табатын қасиеті. Денеге сыртқы әсерлер (күштер) болмаған кезде немесе олар теңгерілген кезде, инерция дененің инерциялық санақ жүйесі деп аталатын жүйеге қатысты өзінің қозғалыс күйін немесе тыныштығын сақтайтындығынан білінеді. Егер денеге күштердің теңгерілмеген жүйесі әсер етсе, онда инерция дененің тыныштық күйі немесе қозғалыс күйі, яғни дене нүктелерініңжылдамдықтары лезде өзгермей, біртіндеп өзгеретіндігін көрсетеді. Бұл жағдайда дене инерциясы неғұрлым көп болса, дене қозғалысы солғұрлым баяу өзгереді. Дене инерциясының өлшемі – масса. Сондай-ақ «инерция» терминін әртүрлі аспаптарға да қолданады. Бұл ретте инерция деп аспаптың белгілі бір тіркелетін шаманы кешіктіріп көрсететіні түсініледі.^[1]

Инерциялық санақ жүйесі – инерция заңы орындалатын санақ жүйесі. Инерциялық санақ жүйесімен салыстырғанда ілгерілемелі, бірқалыпты және түзу сызықты қозғалған кез келген санақ жүйесі де инерциялық санақ жүйесі болады. Сондықтан теория жүзінде, физика заңдары бірдей орындалатын (салыстырмалылық принципі) инерциялық санақ жүйесімен бір мәндес жүйенің саны көп болуы мүмкін. Сондай-ақ кез келген инерциялық санақ жүйесінде Ньютонның 2-заңы және қозғалыс мөлшерінің (импульстің) сақталу заңы, қозғалыс мөлшері моментінің сақталу заңы, т.б. орындалады. Инерциялық санақ жүйесімен салыстырғанда үдей қозғалатын санақ жүйесі инерциялық санақ жүйесі бола алмайды және онда инерция заңы мен жоғарыда аталған заңдар орындалмайды. «Инерциялық санақ жүйесі» ұғымы ғылымиабстракция болып есептеледі. Нақты (реал) санақ жүйесі әрдайым қандайда бір нақты денемен (мысалы, Жермен, кеменің не ұшақтың қорабымен, т.б.) байланыстырылады және оларға қатысты қандайда бір нысанның қозғалысы зерттеледі. Табиғатта қозғалмайтын денелер болмайтындықтан, кез келген нақты санақ жүйесі инерциялық санақ жүйесіне белгілі бір дәрежеде жуық жүйе деп есептелінеді. Инерциялық санақ жүйесінің біреуінен екіншісіне ауысқан кезде, кеңістіктік координаттар мен уақыт үшін Ньютонның классикалық механикасында Галилей түрлендіруі, ал релятивистік механикада Лоренц түрлендірулері орындалады.^[3]

13.Ғарыштық жылдамдық туралы

Ғарыштық жылдамдық — физика мен ғарыш саласында үлкен маңызғы ие түсінік. Ғарыш жылдамдығы дегеніміз аспан денесін (планета) айнала ұшатын ұшу денесінің аспан денесінен (дәлірек, аспан денесі тартылыс күшінен құтылып шығатын) құтылып шығуға қажетті жылдамдығы.

Ғарыштық жылдамдықтар — жасанды денелердің (жерден) бастапкы ұшу жылдамдығы: біріншісі — 7,9 километр/сек., екіншісі — 11,2 километр/сек., үшіншісі — 16,7 километр/сек. Жердің тартылыс күшін теңестіріп, ракетаның жер орбитасын айналып жүруі үшін оған жер бетінде бастапкы жылдамдық беру керек. Ол — 7,9 километр/сек. (шеңбер жылдамдығы). Ракетаның ұшу биіктігі арткан сайын айналудың бастапқы жылдамдығы кемиді (200 километр ұшу биіктігінде — 7,9 километр/сек-ке дейін, 1000 километр биікте — 7,3 километр/сек-ке дейін). Өйткені жердің тартылыс күші азаяды. Жер бетіндегі бастапқы жылдамдықты 7,9-дан 11,2 километр/сек-ке дейін арттырса, ракета эллипс тәрізді орбитада ұшады, оның бір бүйірі жердің орталығында болады. Жылдамдық шеңбер жылдамдығынан артқан сайын, эллипс соғұрлым созылыңқы болады. Жер бетіндегі жылдамдық 11,2 километр/секундке жеткенде, ракета жердің тартылыс күшін женіп, жасанды планетаға айналады. Жер бетіндегі бастапқы жылдамдығы 16,7 километр/секундке жетсе, ракета Жердің де Күннің де тарту күшін жеңіп, күн жүйесінің шеңберінен шығады.^[1]

14.Бірінші ғарыштық жылдамдық

Бірінші ғарыштық жылдамдық (V1) — ұшу денесінің планетаны (аспан денесі) планетаның радиусындай қашықтыққа тастап шығуы үшін қажетті ең төменгі жылдамдық. Басқаша айтқанда, ұшу денесінің планетаны тастап, оның айналасындағы орбитаға барып орналасуы. Бұл жерде атмосфераның кедергісі мен планетаның қозғалысы мен айналу бағыты ескерілмейді.

Бірінші ғарыштық жылдамдыққа ие болып, орбитаға шыққан ұшу денесі планетаның тартылыс күші (гравитация) ықпалымен кері қарай құламай, шеңбер тәріздес орбитасын айнала ұшып жүреді.

Бірінші ғарыштық жылдамдық анықтау (есептеу)

Анықтау әрекетіміз түсінікті болу үшін Жер планетасы мен оны тастап шығатын ұшу денесін қарастырайық.

1) Жердің тартылыс күші аумағында (гравитациялық күш аумағы) ұшып жүрген денеге ол аумақты тастап шығу керек болды. Ол үшін оған, кем дегенде, бірінші ғарыштық жылдамдық керек. Бұл жылдамдық ұшу денесіне әсер ететін екі күшті – центрден тепкіш (центрифугалдық) күш пен гравитациялық тартылыс күші – теңестіру арқылы анықталады.

Формуладағы тұрақтыларды орындарына қойып есептегенде бірінші ғарыштық жылдамдық V1 ≈ 7,91 км/c болады.

2) Жердің еркін түсу үдеуі (g=9,8 м/c²) арқылы да бірінші ғарыштық жылдамдықты анықтай аламыз.

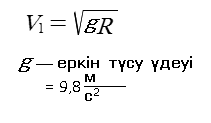
15. Екінші ғарыштық жылдамдық

Жер серігіңнің жылдамдығы бірінші ғарыштық жылдамдықтан сәл асқанда, оның орбитасы эллипс болады,ал жылдaмдық 11,2 км/сек-қа жеткенде, траекториясы, қанаттары шексізге кеткен параболаға айналады. Дененің аспан денесінің тартылыс күшінен босап, шексізге кету мүмкіншілігін тудыратын ғарыштық жылдамдықты екінші ғарыштық жылдмдық деп атайды. Кез келген массасы М, радиусы r аспан денесінің жұлдыз немесе планетаның бірінші ғарыштық жылдамдығын есептейік. Ньютонның екінші заңын және бүкіләлемдік тартылыс заңын ескерсек, бұл дененің r қашықтықтағы еркін түсі үдеуі.

Не нашли, что искали? Воспользуйтесь поиском: