
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Финансовые ренты в страховании
В преобладающем числе областей финансовой деятельности объектами приложения количественных методов анализа являются детерминированные процессы, описываемые верными рентами. Однако в страховании и при анализе некоторых инвестиционных проектов возникает необходимость в использовании условных рент (contingent annuity), в которых фигурируют вероятности наступления соответствующих событий (поступлений или выплат денег). Обсудим методы работы с такими рентами, причем для конкретности ограничимся страхованием. Выплата члена ренты здесь зависит от наступления страхового события. Назовем такие ренты cтраховыми aннуиmеmaми. К страховым, например, относятся все аннуитеты, применяемые в личном страховании. Соответствующие денежные суммы выплачиваются здесь только при жизни (например, пенсии) или, наоборот, смерти застрахованного. Заранее число платежей в таких аннуитетах или их срок остаются неизвестными. Условные аннуитеты являются основным инструментом количественного анализа в страховой деятельности.
Согласно договору страхования страхователь уплачивает вперед страховщику некоторую сумму — премию (premium). В свою очередь он (или его правопреемники) имеет право получить страховую сумму S после наступления страхового события. Если вероятность наступления страхового события q заранее известна (на основании прошлого опыта, по аналогии и т.д.), то теоретически, без учета всех прочих факторов (в том числе и фактора времени), премия P определяется как
P = Sq.
Приведенное равенство лишь иллюстрирует принцип эквивалентности обязательств страхователя и страховщика. В действительности премия обычно превышает величину Sq, так как включает помимо чистой премии и так называемую нагрузку (loading). Последняя охватывает все расходы по ведению дела и некоторую прибыль страховой организации.
Покажем в общем виде, как реализуется этот принцип в страховании жизни при решении важнейшей задачи — расчете тарифной ставки. Напомним, что под тарифной ставкой понимается цена страхования, т.е. цена обязательства уплатить некоторую фиксированную сумму при наступлении страхового случая в расчете на некоторую круглую сумму страховой выплаты (1 тыс. руб., 100 тыс. руб. и т.д.).
Пусть, как и выше, P — размер премии, qn — вероятность страхового события (например, смерть застрахованного через n лет после начала страхования). Речь далее пойдет о нетто-премии, т.е. премии без учета нагрузки. Если страховое событие произойдет на первом году страхования, то страховщик получит сумму P (пусть премии выплачиваются в начале года), если же это событие наступит во втором году, то общая сумма премий составит 2 P и т.д. Математическое ожидание такого ряда премий составит
E (q 1 + 2 q 2 +... + nqn).
Полученная величина хотя и обобщает все выплаты застрахованного с учетом вероятностей их выплат, однако при суммировании соответствующих величин нарушается принцип временной ценности денег, поскольку премии выплачиваются в разные моменты времени. С учетом этого фактора (т.е. с помощью дисконтирования платежей) находим:
Е (А) = P [ q 1 + (1 + v) q 2 + (1 + v + v 2) q 3 +... + (1 + v +... + vn -1) qn ],
где v — дисконтный множитель по ставке i.
Обратимся теперь к выплате страховой суммы. Положим, что она выплачивается в конце года, в котором имел место страховой случай. Тогда математическое ожидание выплаты в первом году составит Sq 1 во втором году — Sq 2 и т.д. Математическое ожидание выплат с учетом времени платежа, очевидно, будет равно:
E (S) = S (vq 1 + v 2 q 2 +... + vnqn).
Исходя из принципаэквивалентности обязательств страховщика и страхователя, теперь можно написать равенство:
E (S) = Е (А),
которое позволяет найти искомое значение нетто-премии и тариф страхования без учета нагрузки. Таков в общем виде теоретический подход к методу расчета премии и тарифа в личном страховании.
Пусть теперь речь идет об имущественном страховании. Если можно полагать, что вероятности наступления страхового случая постоянны, то математическое ожидание суммы премий с учетом их дисконтирования за n лет составит:
Е(А) = P [ q + (1 + v) q +... + (1 + v +... + vn -1)] q.
В свою очередь математическое ожидание выплат страховых сумм находится как
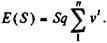
Из равенства математическихожиданий находим размер нетто-премии и тарифной ставки.
Математические ожидания Е (А) и E (S) являются основными характеристиками, с которыми имеют дело в страховании. Они, как видим, представляют собой современные стоимости специфических потоков платежей (платежей с учетом вероятностей их выплат). Причем в имущественном страховании часто это постоянные ренты (при постоянстве вероятностей наступления страховых случаев), а в личном страховании— переменные ренты, поскольку фигурирующие здесь вероятности зависят от возраста застрахованного и меняются для него с каждым годом.
В практике актуарных расчетов (актуарии — страховые математики) разработаны специальные приемы построения упомянутых выше потоков платежей и расчета их математических ожиданий. Рассмотрим их применительно к некоторым видам личного страхования — на дожитие, страхование жизни и, наконец, пенсионное страхование, коль скоро оно сейчас привлекает всеобщее внимание.
До обсуждения проблем построения страховых аннуитетов, связанных с жизнью людей (life annuity), и их использования в страховых расчетах следует ознакомиться с методикой определения необходимых вероятностей и ряда вспомогательных величин, с помощью которых существенно упрощается решение соответствующих задач. Речь пойдет о таблицах смертности и коммутационных функциях.
Таблицы смертности и коммутационные функции. Выше уже было показано, что при разработке страховых потоков платежей необходимы значения вероятностей дожития до определенного возраста или, наоборот, смерти в каком-то возрасте. Систему таких характеристик получают на основе таблицы смертности (mortality table), которая представляет собой числовую модель процесса вымирания некой абстрактной совокупности людей. Основноеее содержание — количества людей каждого возраста (lx), оставшихся в живых из первоначальной совокупности, равной 100 тыс. человек, и число умерших в каждой возрастной группе за год (dx) при некоторых заданных (наблюдавшихся в недавнем прошлом) коэффициентах смертности. Таблицы смертности разрабатываются демографами. В качестве примера приведем фрагмент такой таблицы (мужчины)[4].
| X | lx | qx | dx |
| 0,00196 | |||
| 0,00216 | |||
| 0,00249 | |||
| .... | |||
| 87 779 | 0,00708 | ||
| 87 157 | 0,00770 | ||
| .... | |||
| 65 130 | 0,02871 | ||
| .... | |||
| 43 405 | 0,05691 |
Показатели таблицы смертности связаны очевидными соотношениями:
lx +1 = lx - dx; dx = lx x qx,
где dx — количество умерших в течение года после возраста х лет; qx — вероятность умереть в течение года после возраста х лет.
На основе данных таблицы смертности нетрудно получить систему показателей вероятности дожития, необходимую для создания соответствующих страховых аннуитетов. Определим несколько таких вероятностей. Вероятность прожить по крайней мере еще один год лицу в возрасте х лет равна:

Вероятность дожить от возраста х до х + n составляет:
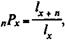
где n — число лет предстоящей жизни.
Пример 6.1. Вероятность двадцатилетнего мужчины дожить до 40 лет составит согласно приведенным в таблице смертности данным
20 P 20 =  = 0,92619.
= 0,92619.
По данным таблицы смертности находят и вероятности умереть в определенных возрастах. Например, вероятность умереть в течение года для лица в возрасте х лет составит:
qx = 1 - px =  , а в возрасте от х до х + п:
, а в возрасте от х до х + п:
nqx = 1 - nPx = 
Для сокращения записи страховых аннуитетов и формул, позволяющих быстро получить необходимые расчетные данные, применяют так называемые коммутационные функции (коммутационные числа). Названные функции делятся на две группы. В основу первых положены числа доживающих до определенного возраста, вторых — числа умерших. Кратко остановимся на методике получения наиболее важных в практическом отношении функций. Основными в первой группе являются функции Dx и Nx:
 (6.1) (6.2)
(6.1) (6.2)
где v — дисконтный множитель по ставке i;
w — предельный возраст, учитываемый в расчете.
Нетрудно получить еще две функции Nx, которые следует применять в случаях, когда выплаты производятся т раз в году. Так, для платежей постнумерандо:
 (6.3) Для платежей пренумерандо:
(6.3) Для платежей пренумерандо:
 (6.4)
(6.4)
Наиболее важными коммутационными функциями второй группы являются Сх и Мх:
 (6.5) (6.6)
(6.5) (6.6)
Примеры коммутационных чисел (т = 12):
| x | lx | Dx | Nx | 
| Cx | Mx |
| 16910,609 | 193931,706 | 202394,583 | 30,448 | 897,899 | ||
| 15483,872 | 177021,097 | 184771,927 | 30,787 | 867,451 | ||
| 12973,771 | 147362,624 | 154459,399 | 30,449 | 836,664 | ||
| ..... | ||||||
| 2794,671 | 28 878,763 | 30 284,048 | 18,167 | 410,185 | ||
| 2545,751 | 26084,094 | 27364,985 | 17,981 | 392,018 | ||
| 369,991 | 2930,070 | 2760,491 | 9,745 | 128,058 | ||
| .... | ||||||
| 104,156 | 650,279 | 602,540 | 5,438 | 50,463 |
Коммутационные числа не следует интерпретировать содержательно. Их, скорее, надо воспринимать как чисто технические, вспомогательные величины. Нельзя забывать и о том, что они существенно зависят от принятой процентной ставки.
Страхование жизни
Для начала рассмотрим самый простой случай личного страхования — страхование на дожитие (pure endowment), которое можно рассматривать как упрощенный вариант пенсионного страхования — страхование одной пенсионной выплаты. Строго говоря, здесь не возникает потребность в страховом аннуитете. Однако обсуждение применяемой методики окажется полезным далее. Итак, человек в возрасте х лет договаривается со страховой организацией о том, что при достижении им 60 лет он получит R рублей. Для определения размера премии найдем математическое ожидание суммы страховки, дисконтированной на срок страхования, т.е. на 60 лет:
60- xEx = R 60- xpxv 60- x
где 60- xpx - вероятность лицу в возрасте х лет дожить до 60 лет.
В общем виде с использованием коммутационной функции Dx получим:
 (6.7)
(6.7)
Влияние принятой процентой ставки здесь очевидно. Чем она выше, тем меньше премия.
Пример 6.2. Необходимо найти стоимость страхования на дожитие до 60 лет мужчины в возрасте 40 лет. Если расчет основывать на процентной ставке, равной 9%, то согласно формуле (6.7) получим:
20 Ex =  = R x 0,13239.
= R x 0,13239.
Премия здесь составляет чуть больше 13% страховой суммы. Полученная величина представляет собой нетто-ставкустрахования на дожитие, т.е. ставку, определенную из условия эквивалентности обязательств страхователя и страховщика. Напомним, что она не учитывает расходов страховщика на ведение дела.
Для того чтобы лучше понять смысл полученных результатов, предположим, что число застрахованных на дожитие равно 1000 человек, а страховая сумма равна 1 млн. руб. Таким образом:
| Число застрахованных | |
| Премия от одного застрахованного | 132390руб. |
| Общая сумма премии | 132 390 тыс. руб. |
| Сумма с процентами за 20 лет | 741 980 тыс. руб. |
| Количество доживших до 60 лет | 742 (741,198) |
| Общая сумма выплат | 742 000 тыс. руб. |
Как видим, наблюдается полная сбалансированность между взносами и выплатами, демонстрирующая соблюдение принципа эквивалентности обязательств страхователей и страховщика (небольшая разница объясняется округлением числа доживших).
Приведенный пример иллюстрирует действие принципа солидарной ответственности страхователей. Дело в том, что страхователь, доживший до 60 лет, часть денег получил за счет тех страхователей, которые не дожили до обусловленного возраста. В самом деле, если бы оговоренную сумму (1 млн. руб.) он обеспечивал самостоятельно (без солидарной ответственности всех участников), то ему необходимо было внести не 132 тыс. руб., а 178 тыс. руб.
Как было показано, в разовом страховании на дожитие страховые аннуитеты не применялись, однако в пенсионном страховании (которое фактически представляет собой многократно повторяемое страхование на дожитие) такие аннуитеты являются исходным материалом для расчета тарифов или размеров пенсий. Об этом более подробно будет сказано в следующем параграфе.
Обратимся теперь к страхованию жизни. Страховая сумма, равная S, выплачивается в случае смерти застрахованного. Допустим, страховой договор заключается в возрасте х лет. Если застрахованный умрет на первом году страхования, а выплата страховой суммы производится в конце этого года, то с учетом вероятности страхового случая современная величина выплаты (на момент заключения контракта) составит qxvS, если страховой случай наступит во втором году, то аналогичная величина равна 2 qxv 2 S и т.д.
Единовременный нетто-тариф определим исходя из принципа эквивалентности обязательств. Искомая величина равна современной стоимости страхового аннуитета или математическому ожиданию суммы дисконтированных выплат. Необходимые для расчета вероятности определим по таблице смертности как dx / lx, dx+ 1/ lx,..., dw / lx. Искомая величина определяется как

Как видим, здесь дисконтируются члены страхового аннуитета. Умножим и разделим каждое слагаемое на vх и используем коммутационную функцию Dx, после чего получим:
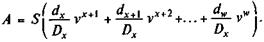
Применив функцию Мх, находим:
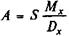 (6.8)
(6.8)
Пример 6.3. Найдем величину премии в виде доли от страховой суммы для сорокалетнего мужчины при немедленном пожизненном страховании жизни:
A = 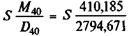 = 0,14677 S.
= 0,14677 S.
Аналогичным путем находятся страховые аннуитеты и тарифы для других условий страхования жизни.
Не нашли, что искали? Воспользуйтесь поиском: