Принцип суперпозиции электрических полей.

Напряженность и потенциал поля, создаваемые в некоторой точке пространства системой точечных зарядов, определяются принципом суперпозиции электрических полей:

, ,

где и φ _i – напряженность и потенциал, создаваемые i -м зарядом в данной точке поля.

Следует учитывать, что линии напряженности поля положительного заряда исходят от него. Линии же напряженности поля отрицательного заряда сходятся на нем (рисунок 1).

Поэтому в одних случаях (точка В) напряженности полей отдельных зарядов суммируют, а в других случаях (точки А и С) вычитают.

Рисунок 1 – Пояснение принципа суперпозиции напряженностей Е

Потенциалы полей складываются с учетом их знаков, как это показано на рисунке 2.

Рисунок 2 – Пояснение принципа суперпозиции потенциалов φ

При решении задач сначала по формулам вычисляются значения напряженностей (или потенциалов), которые создаются в заданной точке (А, В или С) каждым из зарядов (q₁ и q₂). Например, для точки А это будут Е_А1 и Е_А2 (или φ_А1 и φ_А2). Затем полученные значения соответствующих величин складываются с учетом их знаков.

Напряженность и потенциал поля, создаваемого распределенными зарядами.

Если заряд равномерно распределен вдоль линии с линейной плотностью τ, то на линии выделяется малый участок длиной dl с зарядом dq = τdl. Такой заряд можно рассматривать как точечный и применить следующие формулы:

; ,

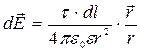где 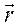– радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.

Используя принцип суперпозиции электрических полей, интегрированием находят напряженность и потенциал φ поля, создаваемого распределенным зарядом:

; .

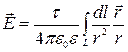Интегрирование ведется вдоль всей длины L заряженной линии.

Интегрирование приводитк следующей формуледля напряженности поля, создаваемого прямой бесконечной равномерно заряженной линией или бесконечно длинным цилиндром:

,

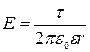где r – расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля;

τ – линейная плотность заряда, τ = q / l.

При расчетах электростатического поля системы зарядов используется теорема Остроградского – Гаусса.

Определение теоремы Остроградского – Гаусса для поля в вакууме: поток вектора напряженности Е электростатического поля через любую замкнутую поверхность S равен алгебраической сумме зарядов , которые охватываются этой поверхностью, деленной на электрическую постоянную.

Математическая формула теоремы имеет следующий вид:

,

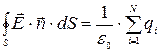где – единичный вектор нормали к элементу поверхности dS.

Если поверхность не охватывает заряд, то поток через такую поверхность равен нулю.

Значение потока вектора Е через замкнутую поверхность не зависит ни от размеров, ни от формы поверхности. Поэтому при расчетах следует выбирать поверхность такой формы, которая позволяет наиболее просто вычислить поток.

Применение теоремы Остроградского – Гаусса к расчету поля приводит к следующим формулам для напряженностей и потенциалов:

напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:

при r < R, E = 0; ;

при r = R, ; ;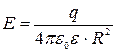

при r > R, ; ,

где q – заряд сферы.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, определяется как

.

Связь потенциала с напряженностью:

в общем случае или ;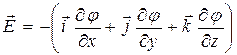

в случае однородного поля ;

в случае поля, обладающего центральной или осевой симметрией,

.

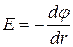Не нашли, что искали? Воспользуйтесь поиском: