Примеры решения задач. Пример 1 Три точечных заряда q1 = q2 = q3 = 1 нКл расположены в вершинах равностороннего треугольника

Пример 1 Три точечных заряда q₁ = q₂ = q₃ = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд q₄ нужно поместить в центре треугольника, чтобы система зарядов находилась в равновесии?

Решение

Все три заряда, расположенные в верши-

нах треугольника, находятся в одинаковых ус-

ловиях. Поэтому достаточно выяснить, какой

заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов,

например q₁, находился в равновесии.

Заряд q₁ будет находиться в равновесии, если векторная сумма действующих на него сил , , 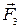равна нулю (рисунок 3):

,

где , , 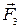– силы, с которыми на заряд q ₁ действуют заряды q ₄, q ₂, q ₃ соответственно;

– равнодействующая сил и .

Так как силы F и F ₄ лежат на одной прямой и направлены в противоположные стороны, то векторное равенство можно заменить скалярным: F – F ₄ = 0, откуда F ₄ = F. Выразив в последнем равенстве F через F ₂ и F ₃ и учитывая, что F ₃ = F ₂, получим

.

Применив закон Кулона и учитывая то, что q ₂ = q ₃ = q ₁, найдем

,

откуда

.

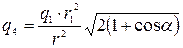Так как треугольник равносторонний, то

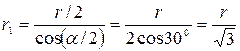, cosα = cos60⁰ = 1/2.

С учетом последних соотношений окончательная формула примет следующий вид

q ₄ = q ₁/ .

Произведем вычисления:

q ₄ = 10^-9/ = 5,77 ∙10^-10 Кл.

Следует отметить, что равновесие системы будет неустойчивым.

Пример 2. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии a = 10 см от ближайшего конца находится точечный заряд q ₁ = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность заряда на стержне.

Решение

Сила взаимодействия F заряженного стержня с зарядом q ₁ зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим на стержне (рисунок 4) малый участок d r с зарядом d q = τ ·d r. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,

.

Проинтегрируем это выражение в пределах от a до a + l

.

Тогда для искомой величины получим

.

Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:

.

Найденная единица является единицей линейной плотности заряда.

Произведем вычисления:

.

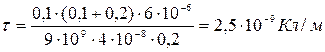Пример 3. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии a ₁ = 0,5 см и a ₂ = 2 см от поверхности цилиндра в средней его части.

Решение

Для определения разности потенциалов воспользуемся формулой, которая связывает напряженность поля с изменением потенциала:

.

Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать как

или . (1)

Интегрируя выражение (1), найдем разность потенциалов двух точек, отстоящих на расстояниях r ₁ и r ₂ от оси цилиндра:

. (2)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:

. (3)

Подставив (3) в (2) для разности потенциалов, получим

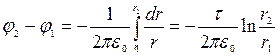
или

.

Произведем вычисления, учитывая то, что величины r ₁ и r ₂, входящие в формулу в виде отношения, можно выразить в сантиметрах (r ₁ = R + a ₁ = 1,5 см, r ₂ = R + a ₂ = 3 см).

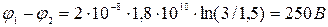
Пример 4. На трех концентрических сферах радиусами R, 2R и 3R распределены заряды с поверхностными плотностями σ ₁, σ ₂ и σ ₃.

Используя теорему Гаусса, найти зависимость E (r) напряженности электрического поля от расстояния для областей 1, 2, 3 и 4 (принять σ ₁ = σ ₃ = σ = 25 мКл/м², σ ₂ = – 25 мКл/м²).

Построить график зависимости E (r).

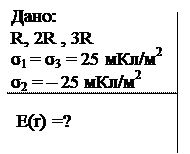
Решение

Теорема Гаусса гласит, что в вакууме поток вектора Е через любую замкнутую поверхность S равен алгебраической сумме зарядов, которые охватываются этой поверхностью, деленной на электрическую постоянную ε ₀. Математическая запись этой теоремы имеет вид:

,

где n – нормаль к элементу поверхности dS;

q – алгебраическая сумма зарядов.

Если выбранная поверхность не охватывает заряды, то поток вектора Е через такую поверхность равен нулю.

По теореме поверхность (гауссова поверхность) может иметь любые форму и размер. Поэтому при расчетах стараются выбрать простые поверхности (сферическую, цилиндрическую и т. д.).

В случае точечного заряда или концентрических заряженных сфер их окружают сферической поверхностью с радиусом r. Тогда интегрирование приводит к такой формуле для потока:

.

По теореме этот поток равен заряду q, деленному на ε ₀:

.

Из последнего выражения получим формулу для напряженности

. (4)

Еще раз уточним, что в формуле (4) величина q – алгебраическая сумма зарядов, которые охватывает проведенная нами гауссова поверхность, а величина r – радиус этой гауссовой поверхности.

Условию задачи соответствует приведенный рисунок 5.

Заряженные сферы показаны сплошными, а гауссовы поверхности в областях 1, 2, 3, 4 –пунктирными линиями.

Используя формулу (4) получим зависимости напряженности поля от расстояния в каждой из областей.

Область 1.

Из рисунка видно, что в области 1 поверхность радиуса r ₁ < R не охватывает заряды. По теореме Гаусса поток вектора Е через эту поверхность равен нулю и напряженность поля в области 1 равна нулю.

E (r ₁) = 0.

Область 2.

Значение радиуса гауссовой поверхности, проведенной в области 2, лежит в пределах

.

Поэтому эта поверхность охватывает только заряд первой сферы и по формуле (4) для напряженности в области 2 получим следующую зависимость:

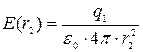, (5)

где q ₁ – заряд первой сферы радиуса R.

В условии задачи дана поверхностная плотность заряда σ ₁, которая связана с зарядом такой формулой

. (6)

Подставив (6) в (5), получим расчетную формулу для области 1:

.

Подставив численные значения величин, получим, что в этой области напряженность поля изменяется от Е (R) = 2,82· 10⁹ В/м при r ₁ = R до Е (2 R) = 0,73 ·10⁹ В/м при r ₁ = 2 R.

Область 3.

В области 3 радиус гауссовой поверхности лежит в пределах . Следовательно, эта поверхность охватывает заряды двух первых заряженных сфер.

По теореме Гаусса в правую часть формулы (4) следует подставить алгебраическую сумму (с учетом знаков) зарядов, первой и второй сфер. Поэтому формула (4) запишется в следующем виде:

. (7)

С помощью (6) выразив заряды сфер q ₁ и q ₂ через поверхностные плотности σ ₁ и σ ₂ и радиусы сфер R и 2 R и подставив в (7), получим зависимость напряженности от расстояния в области 3

. (8)

Подставив в (8) значения, получим, что в этой области напряженность поля изменяется от Е (2 R) = – 2,22· 10⁹ В/м при r ₃ = 2 R до Е (3 R) = – 0,94· 10⁹ В/м при r ₃ = 3 R.

Область 4.

Гауссова поверхность, проведенная в области 4, охватывает заряды всех трех сфер . Поэтому формула (4) запишется в следующем виде:

. (9)

Применив формулу (3), приведем выражение (9) к такому виду:

.

Подставляя численные значения величин, получим значения напряженности на различных расстояниях от сферы 3. В частности, вблизи этой сферы (r ₄ = 3 R) напряженность E (3 R) равна 1,88· 10⁹ В/м.

При известных зависимостях E (r) построение графиков не представляет сложности.

Пример 5. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью υ ₁ = 10⁶ м/с, чтобы скорость его возросла в n = 2 раза.

Решение

Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда e на разность потенциалов U:

A = e∙U. (10)

Работа сил электрического поля в данном случае равна изменению кинетической энергии электрона:

, (11)

где Т ₁ и Т ₂ – кинетическая энергия электрона до и после прохождения ускоряющего поля;

m _e – масса электрона;

υ ₁ и υ ₂ – начальная и конечная скорости электрона.

Приравняв правые части равенств (10) и (11), получим

,

где n = υ ₂/ υ ₁.

Отсюда искомая разность потенциалов

.

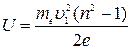Произведем вычисления:

Пример 6. Определить, как распределится напряжение 120 В между тремя последовательно соединенными конденсаторами, имеющими емкости 0,3 мкФ, 0,2 мкФ и 0,12 мкФ

Решение

Для решения задачи используем общую формулу для емкости конденсатора:

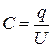, (12)

и формулу емкости батареи последовательно включенных конденсаторов:

. (13)

Также учтем тот факт, что при последовательном соединении заряд каждого из конденсаторов равен заряду батареи q _бат = q _i.

Формулой (12) определяются напряжения как на батарее

, (14)

так и на отдельных конденсаторах

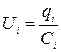. (15)

Из формулы (14) для заряда батареи получим

q _бат = С _бат ∙ U _бат. (16)

Используемые формулы являются основными, и поэтому их размерность можно не проверять

Вычислив по формуле (13) емкость батареи (С _бат = 0,06 мкФ) и подставив это значение в (16) определим заряд батареи: q _бат = 7,2 мкКл. Таким же будет заряд каждого конденсатора: q ₁ = q ₂ = q ₃ = 7,2 мкКл.

Затем, подставляя известные значения емкостей конденсаторов в (15), вычислим искомые напряжения:

U ₁ = 7,2/0,3 = 24 В; U ₂ = 7,2/0,2 = 36 В; U ₃ = 7,2/0,12 = 60 В.

Пример 7. Конденсатор емкостью C ₁ = 3 мкФ был заряжен до разности потенциалов U ₁ = 40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью C ₂ = 5 мкФ. Какая энергия W ' израсходуется на образование искры в момент присоединения второго конденсатора?

Решение

Энергию, израсходованную на образование искры можно определить формулой:

W ' = W ₁ – W ₂,

где W ₁ – энергия, которой обладал первый

конденсатор до присоединения к нему второго конденсатора;

W ₂ – энергия, которую имеет батарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

W = (1/2) C· U ²,

где C – емкость конденсатора или батареи конденсаторов.

Выразив энергии W ₁ и W ₂ через емкости и приняв во внимание то, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим

W΄ = (1/2) C ₁ ·U ₁²–(1/2)(C ₁ + C ₂) U ₂²,(17)

где U ₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что исходный заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U ₂ следующим образом:

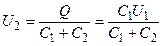. (18)

Подставив выражение (18) в формулу (17) для W ΄, найдем

,

или

.

Произведем вычисления:

W' = .

3.2 Постоянный электрический ток

Электрический ток – это упорядоченное движение электрических зарядов. Характеристикамитока являются сила I и плотность j. Ток с неизменными силой и направлением называется постоянным.

Сила постоянного тока определяется следующим выражением:

,

где q – заряд, который прошел через поперечное сечение проводника за время t.

Плотность постоянного тока вычисляется по формуле

,

где S – площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью направленного движения заряженных частиц

,

где n – концентрация заряженных частиц;

q – заряд частицы.

В случае неразветвленных электрических цепей задачи решаются с помощью законов Ома.

Закон Ома в дифференциальной форме позволяет определить плотность тока в любой точке, где известна напряженность поля.

,

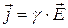где 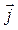– плотность тока;

γ – удельная проводимость;

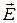– напряженность электрического поля.

Связь удельной проводимости γ с подвижностью b заряженных частиц (ионов):

,

где q – заряд иона;

n – концентрация ионов;

b ₊ и b _- – подвижности положительных и отрицательных ионов.

Законы Ома в интегральной форме определяют силу тока в цепи:

участок цепи, не содержащий ЭДС (однородный участок, рис. 6),

,

где – разность потенциалов (напряжение) на концах участка цепи, ;

R – электрическое сопротивление участка;

участок цепи, содержащий ЭДС (неоднородный участок),

,

где 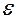– ЭДС источника тока;

R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

замкнутая (полная, рис. 8) цепь,

,

где R – сопротивление нагрузки (потребителя);

r – внутреннее сопротивление (источника тока).

В случае разветвленных цепей их условно разбивают на узлы и контуры, и расчеты проводят с помощью правил Кирхгофа.

Правила Кирхгофадля электрических цепей:

правило для узла – ;

правило для контура – ,

где – алгебраическая сумма сил токов в узле;

– алгебраическая сумма произведений сил токов на отдельных участках контура и сопротивлений этих участков;

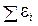– алгебраическая сумма ЭДС в контуре.

Сопротивление R и проводимость G проводника определяются следующими формулами:

; ,

где ρ – удельное сопротивление;

γ – удельная проводимость;

l – длина проводника;

S – площадь поперечного сечения проводника.

Зависимость сопротивления проводника от температуры

,

где R ₀ – сопротивление проводника при нулевой температуре;

α – температурный коэффициент сопротивления;

t – температура.

Сопротивление системы проводников:

– при последовательном соединении;

– при параллельном соединении,

где – сопротивление i -го проводника.

При последовательном соединении источников тока в батарею складываются как их ЭДС

,

так и внутренние сопротивления

.

Параллельное соединение N источников ЭДС используется, как правило, только для одинаковых источников. В этом случае ЭДС батареи равна ЭДС одного источника (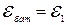), а внутреннее сопротивление батареи равно .

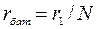Работа электрического тока определяетсяследующими формулами:

– для любого участка цепи, на концах которого поддерживается напряжение U,

,

– для участка, не содержащего ЭДС,

; ,

где I – сила тока;

U – напряжение;

t – время протекания тока.

Мощность тока:

P = I·U, P = I ² ·R, P = U ² /R.

Если по проводнику протекает электрический ток, то проводник будет нагреваться. Количество теплоты Q, которое выделится в проводнике, определяется законом Джоуля – Ленца:

Q = I²·R·t,

где I – сила тока в проводнике;

R – электрическое сопротивление проводника;

t – время протекания тока.

Примеры решения задач

Пример 8. К источнику, имеющему внутреннее сопротивление 2 Ома и ЭДС, равную 12 В, подключены конденсатор емкостью С = 15 мкФ и резистор сопротивлением R = 22 Ом, как показано на рисунке 9.

Чему равен заряд на конденсаторе?

Решение

Заряд конденсатора определяется формулой

q = C ∙ U, (19)

где U – напряжения на обкладках конденсатора.

Так как конденсатор подключен параллельно сопротивлению, то U равно падению напряжения на сопротивлении R. Это падение напряжения определим с помощью закона Ома для участка цепи:

U = I ∙ R, (20)

а силу тока I в цепи – законом Ома для полной цепи:

, (21)

где ε – ЭДС;

r – внутреннее сопротивление источника тока.

Подставив (21) в (20) и затем в (19), получим формулу для искомой величины:

.

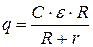Проверим размерность полученной формулы:

.

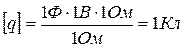Произведем вычисления:

Пример 2. Батарея аккумуляторов, соединенных последовательно, имеет ЭДС 12 В. Ток в цепи 4 А, а напряжение на зажимах 11 В. Определить ток короткого замыкания этой батареи.

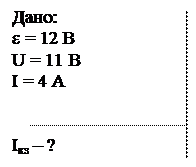Решение

Сила тока в цепи равна силе тока короткого замыкания I _кз при внешнем сопротивлении, равном 0. Из формулы закона Ома для полной цепи

(22)

получим

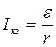, (23)

где ε – ЭДС;

r – внутреннее сопротивление источника;

R – сопротивление нагрузки.

Напряжение на зажимах источника определяется как произведение силы тока и сопротивления нагрузки: U = I ∙ R. Для этого напряжения из (22) получим

. (24)

Выразив из (24) внутреннее сопротивление и подставив его в (23), получим формулу для искомой величины:

.

Размерность полученной формулы очевидна.

Подставив в эту формулу значения величин, получим

А.

Пример 10. Аккумулятор с ЭДС, равной 12 В, и внутренним сопротивлением 1 Ом заряжается при силе тока 3 А.

Найти напряжение на клеммах аккумулятора.

Решение

В общем случае сила I зарядного тока определяется обобщенным законом Ома для неоднородного участка цепи

,

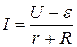где U – напряжение на клеммах аккумулятора;

ε – ЭДС;

r – внутреннее сопротивление аккумулятора;

R – внешнее сопротивление (сопротивление проводов).

Для зарядки аккумуляторов используются провода с малым сопротивлением (толстые провода). Поэтому сила зарядного тока определяется формулой

.

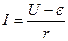Откуда

U = ε + I ∙ r.

Найдем численной значение искомой величины: U = 12+3∙1= 15 В.

Пример 11. Как изменится температура медного стержня, если по нему в течение 0,5 с будет проходить ток, плотность которого 9 А/мм ²?

Решение

Проводник нагревается за счет джоулевой теплоты. Поэтому для решения задачи следует применить закон Джоуля-Ленца

Q = I ²∙ R ∙ t.

Уравнение теплового баланса в этом случае запишется в следующем виде:

I ²∙ R ∙ t = С ∙ m ∙∆ T,

где I – сила тока в проводнике;

R – сопротивление проводника;

t – время протекания тока;

C – теплоемкость материала проводника;

m – масса проводника;

∆T – изменение температуры проводника за время t.

Из формулы теплового баланса выразим искомую величину:

. (25)

Выразим неизвестные величины через известные

, (26)

где j – плотность тока;

S – площадь сечения проводника;

l – длина проводника;

C – удельная теплоемкость материала проводника;

ρ – плотность материала проводника;

ρ _эл – удельное сопротивление проводника.

Подставив (26) в (25), получим

.

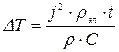Проверим размерность полученной формулы:

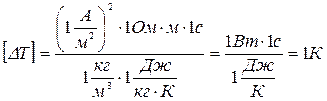
Найдем численное значение величины:

Электромагнетизм

Магнитное поле – это силовое поле, которое возникает вокруг любого движущегося зарядаи проявляется в действии на другие движущиеся заряды. Основной характеристикой магнитного поля является магнитная индукция В. Расчеты магнитной индукции проводят с помощью закона Био-Савара-Лапласа.

Закон Био-Савара-Лапласа определяет индукцию 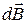магнитного поля, которую создает элемент проводника с током I в некоторой точке А, положение которой определяется радиусом-вектором (рисунок 10).

Формулы закона

в векторной и скалярной формах:

; ,

где – магнитная индукция, которую создает элемент проводника длиной d l с током I в некоторой точке А пространства;

– радиус-вектор, направленный от элемента проводника в точку А, в которой определяется магнитная индукция;

α – угол между радиусом-вектором и направлением тока в элементе проводника;

μ ₀ – магнитная постоянная, μ ₀ = 4π∙ 10^-7 Гн/м;

μ – магнитная проницаемость среды, где находится проводник.

Направление вектора магнитной индукции, определяется по правилу правого винта.

Магнитная индукция, создаваемая проводниками с различными формой и размером, определяется интегрированием по всей длине проводника. Ниже приводятся результаты интегрирования для разных проводников.

Не нашли, что искали? Воспользуйтесь поиском: