Магнитная индукция поля внутри соленоида

,

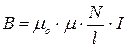где N – число витков;

l – длина соленоида.

Связь магнитной индукции с напряженностью магнитного поля:

,

где μ – магнитная проницаемость изотропной среды.

Если к незакрепленному проводнику с током поднести постоянный магнит, то проводник будет смещаться. Сила, которая действует в этом случае на проводник, определяется з аконом Ампера.

В случае прямолинейного проводника с током и однородного магнитного поля формула закона Ампера имеет следующий вид:

, или ,

где l – длина проводника;

α – угол между направлением тока в проводнике и вектором магнитной индукции .

Направление силы Ампера определяется правилом левой руки.

Если поле неоднородно и проводник не является прямым, то закон Ампера записывается для элемента dl проводника как

.

Силу, действующую на весь проводник, определяют интегрированием:

.

За счет силы Ампера проводник с током занимает определенное положение в магнитном поле.

Механический (вращательный) момент М, действующий на контур с током, помещенный в однородное магнитное поле,

или ,

где 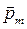– магнитный момент контура с током;

– магнитная индукция поля;

α – угол между векторам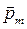и и .

Магнитный момент плоского контура с током

,

где – единичный вектор нормали (положительной) к плоскости контура;

I – сила тока, протекающего по контуру;

S – площадь, охватываемая контуром.

Потенциальная энергия (механическая) контура с током в магнитном поле

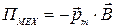, или .

Сила Лоренца – это сила, которая действует на частицу с зарядом q, движущуюся со скоростью υ в магнитном поле с индукцией В.

или ,

где – скорость заряженной частицы;

α – угол между векторами и .

Направление силы Лоренца определяется правилом левой руки, и эта сила всегда перпендикулярна скорости частицы. Поэтому сила Лоренца является центростремительной и справедливо следующее соотношение:

,

где m – масса частицы;

R – радиус кривизны траектории.

Если частица движется перпендикулярно силовым линиям однородного магнитного поля (В = const), то траектория представляет собой окружность радиусом R.

Закон полного тока для магнитного поля позволяет определить магнитную индукцию, которая создается системой проводников.

Закон формулируется следующим образом: циркуляция 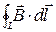вектора магнитной индукции по любому замкнутому контуру L равна магнитной постоянной µ₀, умноженной на алгебраическую сумму токов I _i, которые охватываются данным контуром:

.

Например, если контур охватывает три проводника с токами I ₁ и I ₂, направленными в одну сторону, и током I ₃, направленным в противоположную сторону, то алгебраическая сумма токов

.

Если выбранный контур не охватывает проводников с током, то циркуляция вектора В по такому контуру равна нулю.

Магнитный поток равен числу линий магнитной индукции, которые пересекают данную поверхность.

В случае однородного магнитного поля и плоской поверхности магнитный поток определяется следующей формулой:

,

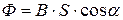где S – площадь контура;

α – угол между нормалью к плоскости контура и вектором магнитной индукции.

В общем случае неоднородного поля и произвольной формы поверхности поток через нее определяют интегрированием:

,

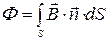где – единичный вектор нормали к элементу dS поверхности.

Работа по перемещению проводника с током в магнитном поле вычисляется по формуле

,

где – магнитный поток через поверхность, которую очерчивает проводник при своем движении (число силовых линий, которые пересекает проводник).

Электромагнитная индукция – это явление возникновения ЭДС в контуре при изменении магнитного потока через его поверхность.

ЭДС индукции определяется законом электромагнитной индукции

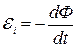или .

Если взять производную по времени от магнитного потока, то можно получить такую формулу для ЭДС индукции

.

Первое слагаемое полученной формулы определяет ЭДС, которая возникает при изменении индукции магнитного поля, второе слагаемое связано с изменением площади контура, третье слагаемое характеризует ЭДС, возникающую при изменении положения контура.

Частным случаем электромагнитной индукции является возникновение разности потенциалов на концах проводника, движущегося в магнитном поле. Эта разность потенциалов определяется следующей формулой:

,

где В – индукция магнитного поля;

l – длина проводника;

– скорость проводника;

α – угол между векторами и .

Заряд q, протекающий по замкнутому контуру (катушке) при изменении магнитного потока , пронизывающего этот контур (катушку):

или ,

где N – число витков катушки;

R – электрическое сопротивление контура (катушки).

Самоиндукция – это частный случай электромагнитной индукции.

Самоиндукция – это явление возникновения ЭДС (индукционного тока) в контуре, по которому течет переменный ток.

В этом случае магнитный поток Ф через контур определяется силой тока I, протекающего по контуру:

,

где L – индуктивность.

Формула для индуктивности соленоида имеет вид

,

где µ – магнитная проницаемость среды;

µ₀ – магнитная постоянная;

N – число витков на длине l соленоида;

S – площадь витка.

ЭДС самоиндукции определяется следующей формулой:

.

По правилу Ленца индукционный ток во всех случаях препятствует изменению основного тока. Это приводит к замедлению нарастания силы тока при замыкании и ее убывания при размыкании цепи.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

при замыкании цепи

,

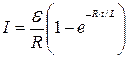где – ЭДС источника тока;

t – время, прошедшее с момента замыкания цепи;

при размыкании цепи

,

где I ₀ – сила тока в цепи в момент размыкания (при t = 0);

t – время, прошедшее с момента размыкания цепи.

При прохождении электрического тока по проводнику часть энергии источника тока переходит в энергию магнитного поля.

Не нашли, что искали? Воспользуйтесь поиском: