Примеры решения задач. Пример 12.Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой I = 60 А

Пример 12. Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d =10 см друг от друга. Определить магнитную индукцию B поля, создаваемого проводниками с током в точке А (рисунок 12), отстоящей от оси одного проводника на расстоянии r ₁ = 5 см, от другого – r ₂ =12 см.

Решение

Для нахождения магнитной индукции B в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций B ₁ и B ₂ полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:

.

Модуль вектора может быть найден по теореме косинусов:

, (27)

где α – угол между векторами 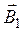и .

Магнитные индукци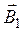и и выражаются через силу тока I и расстояния r ₁ и r ₂ от проводника до точки А соответственно:

B ₁ = μ ₀ I /(2π r ₁); B ₂ = μ ₀ I /(2π r ₂).

Подставляя выражения B ₁ и B ₂ в формулу (27) и вынеся μ ₀ I /(2π) за знак корня, получим

.

Вычислим cos α. Заметив, что α – это угол DAC, по теореме косинусов запишем

,

где d – расстояние между проводами. Откуда

; .

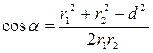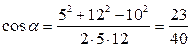Произведем вычисления:

Пример 13. Короткая катушка, содержащая N = 10³ витков, равномерно вращается с частотой n = 10 с^-1 относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям однородного магнитного поля (B = 0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол α = 60⁰ с линиями поля. Площадь S катушки равна 100 см².

Решение

Мгновенное значение ЭДС индукции ε определяется основным уравнением электромагнитной индукции Фарадея – Максвелла

, (28)

а потокосцепление ψ = NФ,

где N – число витков катушки, пронизываемых магнитным потоком Ф. Подставив выражение ψ в формулу (28), получим

. (29)

При вращении катушки магнитный поток Ф, пронизывающий катушку в момент времени t, изменяется по закону

Ф = B · S ·cos(ω ∙ t),

где B – магнитная индукция;

S – площадь катушки;

ω – угловая скорость катушки.

Подставив выражение для магнитного потока Ф в (29) и продифференцировав полученную формулу по времени, найдем мгновенное значение ЭДС индукции:

.

Учитывая то, что угловая скорость ω связана с частотой вращения n катушки соотношением ω = 2π· n и угол ω·t = π/2 – α, получим

.

Анализ размерности:

.

Произведем вычисления:

ε = 2∙3,14∙10∙10³∙0,04∙10^-2∙0,5 = 25,1 В.

Пример 14. Соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида.

Решение

Индуктивность L связана с потокосцеплением ψ и силой тока I соотношением

ψ = L∙I. (30)

Потокосцепление, в свою очередь, может бытьопределено через поток Ф и число витков N (при условии, что витки плотно прилегают друг к другу):

ψ = N∙Ф. (31).

Приравняв (30) и (31), найдем формулу для индуктивности соленоида:

L = N∙Ф/I. (32)

Энергия магнитного поля соленоида определяется формулой

W = 1/2(L∙I ²). (33)

Подставив в формулу (33) вместо индуктивности выражение (32), получим формулу для расчета энергии соленоида:

W= 1/2(N∙Ф∙I).

Произведем вычисления:

;

.

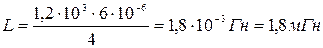Колебания и волны

Колебание – это процесс, который повторяется с течением времени.

При гармонических колебаниях значения физических величин изменяются по закону синуса или косинуса.

Кинематика колебаний описывается кинематическим уравнением гармонических колебаний, котороеимеет вид:

S (t) = A ·cos(ωt + φ ₀),

где S – мгновенное значение колеблющейся величины, при механических колебаниях S – смещение от положения равновесия;

А – амплитуда колебания (максимальное значение величины S);

(ωt + φ ₀) – фаза колебания;

ω – угловая или циклическая частота колебания;

φ ₀ – начальная фаза колебания.

Динамика колебаний описывается следующим дифференциальным уравнением гармонических колебаний:

.

Решением этого уравнения является приведенное выше кинематическое уравнение.

Быстрота изменения колеблющейся величины определяется скоростью υ и ускорением а, которые вычисляются по формулам:

где A · ω – амплитудное (максимальное) значение скорости;

A · ω ² – амплитудное (максимальное) значение ускорения.

Следует иметь в виду, что приведенными уравнениями описываются как механические, так и электромагнитные колебания. Например, при электрических колебаниях первая производная от уравнения колебания заряда дает уравнение колебания силы тока:

Не нашли, что искали? Воспользуйтесь поиском: