
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сложные ставки ссудных процентов
Если после очередного интервала начисления доход (т. е. начисленные заданный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.
Пусть i с - относительная величина годовой ставки сложных ссудных процентов; k н.с.- коэффициент наращения в случае сложных процентов; j - номинальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).
Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (12.10) составит:

Еще через год это выражение применяется уже к сумме:

и так далее. Очевидно, что по прошествии лет наращенная сумма составит:

Множитель наращения k н.с.соответственно будет равен:

При начислении простых процентов он составил бы:

Если срок ссуды в годах не является целым числом, множитель наращения определяют по выражению:

где n = n a + n b;
n a - целое число лет:
n b - оставшаяся дробная часть гола.
На практике в данном случае часто предпочитают пользоваться формулой 12.22 с соответствующим нецелым показателем степени. Но нужно иметь в виду, что исходя из сущности начисления процентов этот способ является приблизительным, и погрешность при вычислениях будет тем больше, чем больше значения входящих в формулу величин. Следует учитывать, что приблизительный метод дает меньший, чем в действительности, результат.
При N интервалах начисления наращенная сумма в конце всего периода начисления составит:
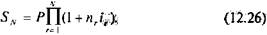
Если все интервалы начисления одинаковы (как и бывает обычно на практике) и ставка сложных процентов одна и та же, формула (12.25) принимает вид:

Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j - годовая ставка, по которой определяется величина ставки процентов, применяемой на каждом интервале начисления.
При т равных интервалах начисления и номинальной процентной ставке j эта величина считается равной j / m.
Если срок ссуды составляет лет, то аналогично (12.21) получаем выражение для определения наращенной суммы:

Здесь mn - общее число интервалов начисления за весь срок ссуды.
Для целого числа периодов начисления используется формула сложных процентов (12.21), а для оставшейся части - формула простых процентов (12.10).
В нашей стране в настоящее время наиболее распространено начисление процентов по полугодиям, поквартальное и ежемесячное (иногда интервалом начисления может быть и день). Такие проценты, начисляемые с определенной периодичностью, называются дискретными.
В мировой практике часто применяется также непрерывное начисление сложных процентов (т. е. продолжительность интервала начисления стремится к нулю, а m - к бесконечности).
В этом случае для вычисления наращенной суммы служит выражение:

Для расчетов можно использовать формулу:

Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях (т.е. при одинаковых п, j, Р).
Также из формулы (12.22) имеем:

а из формулы (12.28)

Применяя операцию логарифмирования к обеим частям формулы (12.22). получаем:

Подобным же образом из формулы (12.24) получаем

Организация долгосрочного кредитования базируется на трех основополагающих принципах: обеспеченности, срочности, платности. Коммерческий банк кредитует только такие мероприятия, которые имеют реальные сроки окупаемости и наличие источников возврата кредита, обеспечивают окупаемость финансируемых вложений в более короткие сроки, чем среднеотраслевые сроки окупаемости. Банковский кредит, в отличие от бюджетного финансирования, позволяет повысить эффективность инвестиционных мероприятий и в целом ряде случаев может оказаться более приемлемым и удобным методом мобилизации денежных средств на длительные сроки, чем выпуск корпоративных акций или размещение облигационных займов.
Вопросы для самоконтроля
1. Дайте определение экономическим категориям «эффект» и «эффективность».
2. Какие три вида эффекта может дать внедрение инноваций?
3. Что означает экономическая эффективность инноваций?
4. Какие основные характеристики производства изменяют инновации?
5. Перечислите типы показателей эффективности инноваций, которые используют в производственной сфере?
6. Какие ситуации характерны дли экономической эффективности нововведений затратного и ресурсного типов?
7. Охарактеризуйте показатели эффективности инвестиционного проекта.
8. Назовите статистические методы оценки эффективности.
9. Перечислите динамические показатели опенки эффективности.
Не нашли, что искали? Воспользуйтесь поиском: