Метод взятия обратной функции

Допустим, что нам задан интегральный закон распределения вероятности F (x), где f (x) — функция плотности вероятности и

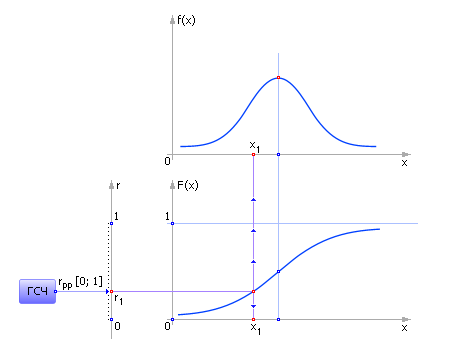
Тогда достаточно разыграть случайное число, равномерно распределенное в интервале от 0 до 1. Поскольку функция F тоже изменяется в данном интервале, то случайное событие x можно определить взятием обратной функции по графику или аналитически: x = F^–1(r). Здесь r — число, генерируемое эталонным ГСЧ в интервале от 0 до 1, x ₁ — сгенерированная в итоге случайная величина. Графически суть метода изображена на рис. 24.6.

Рис. 24.6. Иллюстрация метода обратной функции для генерации случайных событий x, значения которых распределены непрерывно. На рисунке показаны графики плотности вероятности и интегральной плотности вероятности от х

Данным методом особенно удобно пользоваться в случае, когда интегральный закон распределения вероятности задан аналитически и возможно аналитическое взятие обратной функции от него, как это и показано на следующем примере.

Пример 1. Примем к рассмотрению экспоненциальный закон распределения вероятности случайных событий f (x) = λ · e ^{– λx} . Тогда интегральный закон распределения плотности вероятности имеет вид: F (x) = 1 – e ^{– λx} .

Так как r и F в данном методе предполагаются аналогичными и расположены в одном интервале, то, заменяя F на случайное число r, имеем: r = 1 – e ^{– λx} .

Выражая искомую величину x из этого выражения (то есть, обращая функцию exp()), получаем: x = –1/ λ · ln(1 – r).

Так как в статическом смысле (1 – r) и r — это одно и тоже, то x = –1/ λ · ln(r).

На рис. 24.7 показан фрагмент алгоритма, реализующего метод обратной функции для экспоненциального закона.

Рис. 24.7. Фрагмент блок-схемы алгоритма, реализующей метод обратной функции для экспоненциального закона

Не нашли, что искали? Воспользуйтесь поиском: