ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Технология выполнения работы
Основы алгоритмизации
Basics of Algoritms
Құрастырушылар: аға оқытушылар
Қойшыбекова А.К., Жексембаева Р.Ж.
Составители: ст.преподаватели
Жексембаева Р.Ж., Койшыбекова А.К.
Сompilers: senior lectures
R.Zheksembayeva, A.Koyshybekova
Taлдықорған, 2015
Талдыкорган, 2015
Тaldykorgan, 2015
Содержание
| Практическая работа 1. Этапы решения задач на ЭВМ | |
| Практическая работа 2. Построение алгоритмов | |
| Практическая работа 3. Построение алгоритмов разветвляющейся конструкции | |
| Практическая работа 4. Построение алгоритмов циклической конструкции | |
| Практическое занятие 5. Построение алгоритмов сортировки | |
| Практическое занятие 6. Построение машины Тьюринга | |
| Практическое занятие 7. Построение машины Поста | |
| Практическое занятие 8. Написание линейных программ в QBasic | |
| Практическая работа 9. Составление программ с условным оператором | |
| Практическая работа 10. Операторы цикла в QBasic | |
| Практическая работа 11. Операторы цикла while | |
| Практическая работа 12-13. Построение графических объектов в QBasic | |
| Практическая работа 14-15. Решение задач со строками |
Практическая работа 1. Этапы решения задач на ЭВМ
Цель: Ознакомиться с этапами решения задач на ЭВМ.
Задание 1. Заполните таблицу - Ученые в истории алгоритмов
| № | Ученый | Вклад в историю развития алгоритмов |
| Эратосфен | ||
| Мухамед аль-Хорезми | ||
| Евклид | ||
| Лейбниц | ||
| А. Тьюринг | ||
| Э. Пост | ||
Задание2: Заполните таблицу - Этапы решения задач на ЭВМ
| № | Название этапа | Описание этапа |
| Постановка задачи | ||
| Построение математической модели | ||
| Разработка алгоритма | ||
| Запись алгоритма на языке программирования | ||
| Отладка и тестирование программы на компьютере | ||
| Анализ полученных результатов. |
Задание 3. Составьте ассоциограмму «Алгоритм»
 |
Задание 4. Вычислить количество краски для покрытия пола в спортивном зале. Составить математическую модель задачи.
Методика выполнения задания 4.
Этапы решения задачи на ЭВМ
1. Постановка задачи
При покраске пола стараются, чтобы слой краски покрывал поверхность равномерно. Для выполнения этого задания измеряют длину пола. Это значит, что количество краски пропорционально площади, которую надо покрасить. Поэтому, для решения задачи нужно знать площадь пола. Существенным является предположение: пол имеет форму прямоугольника. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.
2. Математическая модель
Пусть A – длина пола, B - ширина пола, S1 - площадь, которую можно покрыть содержимым одной банки, N – количество банок, тогда:
площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.
Задача 5
На научный семинар собрались ученые и обменялись друг с другом визитными карточками. Всего было роздано 210 визитных карточек. Сколько ученых приехало на семинар, если известно, что их было не более 20? Составить математическую модель задачи
Задачи для самостоятельного решения
1. Участники шахматного турнира после окончания очередной партии обменивались друг с другом рукопожатиями. Всего сыграно 210 партий, значит, 210 раз противники жали друг другу руки. Сколько человек принимали участие в турнире, если каждый сыграл по одному разу со всеми остальными и известно, что участников было не более 38? Составить математическую модель задачи.
2. Дана правильная дробь, знаменатель которой на 2 больше числителя. Если от числителя отнять 1, а к знаменателю прибавить 7 и сократить дробь, то в результате получится 1/2. Найти исходную дробь. (Используется таблица задачи №4, изменив соответствующим образом формулы в ячейках).
3. Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Удастся ли это сделать?
4. 1) Площадь прямоугольного треугольника равна 6 см. Найти длины катетов и гипотенузы этого треугольника, если один катет больше другого на 1 см и известно, что длина каждой из сторон не превосходит 12 см.
Составьте в тетради математическую модель этой задачи:
• выделите исходные данные;
• определите, что является результатом;
• найдите связь между исходными данными и результатом и запишите ее в виде математических соотношений (представьте в виде уравнения).
5. 1) Повторить формулы площади боковой поверхности и объема параллелепипеда.
6. Требуется оббить входную дверь 210х92 см дерматином. Хватит ли куска дерматина 215х102 см для обивки двери, если на подгиб с каждой стороны требуется по 2 см ткани?
7. Необходимо покрасить краской панели (стены) кухонной комнаты. Сколько потребуется банок краски, если размеры кухни: 405х310х285 см, 88% площади стены занимает кафельная плитка и 1 банка краски предназначена для покраски площади 5 м2?
Контрольные вопросы:
1. Что такое математическое моделирование?
2. Дайте определение математической модели.
3. Перечислите этапы решения задачи на компьютере.
4. Опишите алгоритм Евклида
Практическая работа 2. Построение алгоритмов
Цель: изучить свойства алгоритмов и методы построения алгоримтов
Задание 1: Заполните таблицу – Свойства алгоритмов:
| № | Свойство алгоритма | Характеристика свойства |
| Детерменированность | ||
| Массовость | ||
| Результативность | ||
| Дискретность | ||
| Конечность | ||
| Корректность |
Задание 2: Вычислить периметр произвольного треугольника по его трем сторонам (вопрос существования треугольника не рассматривается).
Методика выполнения задания 2:
1 этап: Постановка задачи.
Исходные данные: А, B, C – стороны произвольного треугольника
Выходные данные: P – периметр треугольника.
2 этап: Математическая модель.
P=A+B+С
3 этап: Составление алгоритма
Рис. 1. Пример линейного алгоритма
Задачи для самостоятельного решения
Задание 2. Составить алгоритм решения задачи с помощью словесного алгоритма, блок-схем
1. Вычислить площадь поверхности и объем усеченного конуса по следующим формулам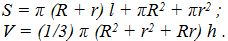 
2. Вычислить координаты центра тяжести трех материальных точек с массами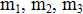 
и координатами
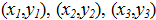по формулам:
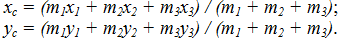
3. Вычислить площадь треугольника со сторонами a, b, c по формуле Герона:
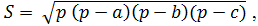
где p – полупериметр, вычисляемый по формуле (a+b+c)/2.
4. Вычислить координаты точки, делящей отрезок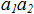 
в отношении 
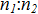по формулам:
где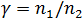 
.
5. Вычислить медианы треугольника со сторонами a, b, c по формулам:
6. Вычислить площадь круга и длину окружности по введенному значению радиуса.
7. Вычислить площадь S и периметр L эллипса по введенным значениям полуосей a и b:
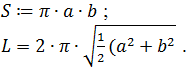
8. Вычислить объем V и площадь боковой поверхности цилиндра S по введенным значениям радиуса основания R и высоты цилиндра H.
9. Вычислить объем V и площадь боковой поверхности конуса S по введенным значениям радиуса основания r, высоты h и образующей l:
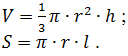
10. Вычислить объем V и площадь поверхности S сферы по введенному значению радиуса r:
11. Дано целое четырехзначное число. Используя операции div и mod, найти сумму его цифр.
12. Дана сторона равностороннего треугольника. Найти площадь этого треугольника и радиусы вписанной и описанной окружностей.
13. Даны координаты трех вершин треугольника (x1, y1), (x2, y2), (x3, y3). Найти его периметр и площадь.
14. Дана длина окружности. Найти площадь круга, ограниченного этой окружностью.
15. Дана площадь круга. Найти длину окружности, ограничивающей этот круг.
Технология выполнения работы
В рамках выполнения работы необходимо составить алгоритм решения задачи в виде блок-схемы и с помощью блок схем
Содержание отчета
1. Цель работы и задание.
2. Условие задачи.
3. Алгоритм, написанный с помощью псевдокода и блок- схемы.
Вопросы для защиты работы
1. Что такое алгоритм?
2. Свойства алгоритма.
3. Способы записи алгоритма.
4. Основные элементы блок-схемы.
5. Виды алгоритмов.
6. Отличительные особенности алгоритмов с предусловием и постусловием.
Практическая работа 3. Построение алгоритмов разветвляющейся конструкции
Цель: приобрести навыки построения разветвляющихся алгоритмов на алгоритмическом языке и на языке блок-схем.
Задание 1. Вычислить значение функции 
для заданного x.
Методика выполнения задания 1:
1 этап: Постановка задачи.
Исходные данные: x – значение аргумента функции.
Выходные данные: y – искомое значение функции при заданном x.
2 этап: Математическая модель.
3 этап: Составление алгоритма на языке блок -схем
Рис. 2. Пример разветвляющегося алгоритма
Составление алгоритма на алгоритмическом языке:
Алг функция
арг х
рез у
нач
если х<=10 то у=-5
иначе у=х3
кон.
Задачи для самостоятельного решения
Задание 2. Составить алгоритм решения задачи с помощью алгоритмического языка и составьте блок схему:
1. Составить программу для решения квадратного уравнения ax2 + bx + c = 0.
2. Определить максимальное четное число из двух введенных.
3. Определить, можно ли из отрезков с длинами х, y и z построить треугольник.
4. Ввести два числа а и b. Большее число заменить утроенным произведением, меньшее – полусуммой.
5. Если среди трех чисел a, b, c имеется хотя бы одно четное, то найти максимальное число, иначе – минимальное.
6. Определить, в каком квадранте находится точка с координатами x и y и вывести номер квадранта на экран.
7. Найти квадрат наибольшего из двух чисел а и b. Вывести на экран число 1, если наибольшим является число а, число 2 – если наибольшим числом является b.
8. Определить, попадает ли точка с координатами x и y в круг радиусом R. Если точка попадает в круг, вывести на экран единицу, в противном случае – ноль.
9. Написать алгоритм решения задачи, которая решает уравнение ax + b = 0 относительно x для любых чисел a и b, введенных с клавиатуры. Все числа считаются действительными.
10. Написать алгоритм решения задачи, которая определяет, лежит ли точка А(х,у) внутри некоторого кольца («внутри» понимается в строгом смысле, т.е. случай, когда точка А лежит на границе кольца, недопустим). Центр кольца находится в начале координат. Для кольца заданы внутренний и внешний радиусы r1, r2. Координаты x и у вводятся с клавиатуры.
11. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной произведение этих значений, а если равны, то присвоить переменным нулевые значения.
12. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной минимальное из этих значений, а если равны, то присвоить переменным нулевые значения.
13. Даны целочисленные координаты точки на плоскости. Если точка не лежит на координатных осях, то вывести 0. Если точка совпадает с началом координат, то вывести 1. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 2 или 3.
14. Даны вещественные координаты точки, не лежащей на координатных осях OX и OY. Вывести номер координатной четверти, в которой находится данная точка.
15. Дано целое число, лежащее в диапазоне от –999 до 999. Вывести строку – словесное описание данного числа вида "отрицательное двузначное число", "нулевое число", "положительное однозначное число" и т.д.
Не нашли, что искали? Воспользуйтесь поиском: