
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Функции для работы со строками
| Функция | Назначение | Описание |
| LCASE$ (символьное_выражение) | Функция, возвращающая символьную строку, в которой все латинские буквы преобразованы в строчные | CLS READ Word$ PRINT LCASE$(Word$) DATA “THIS IS THE STRING in lower case” |
| UCASE$ (символьное_выражение) | Функция, возвращающая символьное значение, в котором все латинские буквы – заглавные. | |
| LTRIM$ (символьное_выражение) | Возвращает копию строки с удаленными начальными пробелами | |
| RTRIM$ (символьное_выражение) | Возвращает символьную строку с удаленными правыми пробелами | |
| SPACE$ (n) | Возвращает строку пробелов длиной n | |
| STRING$ (m, n) STRING$ (m, символьное_выражение) | Возвращает строку, заполненную символами данного ASCII – кода или данным символом | m – числовое выражение, длина строки n – числовое выражение в пределах 0-255, код символа – заполнителя символьное_выражение – указывает строку, первый символ которой используется для заполнения строки |
| INSTR ([начало, ] строка 1, строка 2) | Возвращает позицию первого вхождения подстроки в указанной строке | Начало – смещение от начала строки Строка 1 – строка, в которой производится поиск Строка 2 – искомая строка |
| LEFT$(символьное_выражение, n) RIGHT (символьное_выражение, n) | Возвращает строку, содержащую n левых / правых символов исходной строки | CLS A$ = “QBasic Forever!” B$ = LEFT$ (A$, 5) PRINT B$ |
| MID$ (символьное_выражение, начало [, длина]) | Функция, возвращает фрагмент указанной строки | символьное_выражение – указанная строка начало – позиция начала длина – длина фрагмента |
| STR$ (числовое выражение) | Возвращает символьное представление числа или числового выражения | |
| LEN (символьное_выражение) | Возвращает количество символов данной строки. |
Пример: преобразование имени вида «Имя Фамилия» в форму «Фамилия Имя»
CLS
LINE INPUT “Имя: “; Nm$
Sposs=INSTR(1, Nm$, “ ”)
IF Sposs=0 THEN
PRINT Nm$ ‘введена только фамилия
ELSE
Lastname$=RIGHT$(Nm$, LEN(Nm$)-Sposs)
Firstname$=LEFT$(Nm$, Sposs-1)
PRINT Lastname$; “,“; Firstname$
END IF
END
Задания
1. Напишите программу, заменяющую два и более пробела в строке на один.
2. Напишите программу, выводящую строку в обратном программе.
3. Задана строка символов. Подсчитайте количество символов «k» в строке.
4. Напишите программу, заменяющую все заглавные буквы в строке на строчные.
5. Напишите программу, подсчитывающую количество предложений в тексте.
6. Напишите программу, которая подставляет в конце каждой строки ее порядковый номер.
Контрольные вопросы:
1. Какой тип данных называется символьным?
2. Каким образом присваивают символ переменной в Паскале?
3. В виде чего хранятся в памяти символьные переменные?
4. Какой тип данных в Паскале называется строковым?
5. Как сравниваются строки?
Список использованной литературы
Основная литература
1. Языки программирования [Текст] = The c Programming language / В. Керниган, Д. Риччи.- PH PTR, 2014.- 271p
2. Алгоритмы, структуры данных и программирование [Текст]: Курс лекций / Л.С. Криванкова.- Талдыкорган: ЖГУ им.И.Жансугурова, 2015
3. Бобровский С. Программирование на языке QBasic для школьников и студентов. - М.: ДЕСС КОМ, 2000.
4. Культин Н. Основы программирования. – СПб: БХВ-Петербург, 2012 – 608с
5. Лавров С. Программирование. Математические основы, средства, теория. – СПб.: БХВ-Петербург, 2013.–320 с
Дополнительная литература
1. Абрамов С.А. и др. Задачи по программированию.-М.:Наука, 2014
2. Гуденко Д. Петроченко Д. В. Сборник задач по программированию.-Спб, Питер, 2012
3. Visual Basic 5 [Text].- СПб.: Питер, ВНҮ,.- 976 с: с дискетой
Карлоф, Х.
4. Линейное программирование [Text] = Linear Programming / Х. Карлоф.- Boston: Birkhauser, - 142с.
5. В.Б.Попов, Турбо Паскаль, М: Финансы и статистика, 2012
6. Гуденко Д. Петроченко Д. В. Сборник задач по программированию.-Спб, Питер, 2012
7. Светозарова Г.И., Мельников А.А., Козловский А.В. Практикум по программированию на языке Бейсик.-М: Наука, 2012
8. 6. Фаронов В.В. Программирование на персональных ЭВМ в среде ТУРБО-ПАСКАЛЬ. – М.: Изд.-во МГТУ, 2013. – 580 с.
Содержание
| Practical work 1.Stages of problem solving by computer. | |
| Practical work 2.Construction of algorithms | |
| Practical work 3.Construction of algorithms branching structure | |
| Practical work 4.Construction of a cyclic structure algorithms | |
| Practical work 5.Construction of sorting algorithms | |
| Practical work 6.Construction of the Turing machine | |
| Practical work 7.Construction of the Post machine | |
| Practical work 8.Linear programming in QBasic | |
| Practical work 9.Drawing up a program with the conditional operator | |
| Practical work 10.Operators of the cycle in QBasic | |
| Practical work 11.Operators -while of the cycle | |
| Practical work 12-13. Construction of graphic objects in QBasic | |
| Practical work 13. Solving problems with strings |
Practical work 1. Stages of problem solving by computer.
Objective: To familiarize with the stages of solving problems on computers.
Task 1. Fill in the table - Scientists in the history of algorithms
| № | Scientist | Contribution to the history of the development of algorithms |
| Eratosthenes | ||
| Mohamed Al-Khwarizmi | ||
| Euclid | ||
| Leibniz. Turing | ||
| I. Post | ||
| Scientist | ||
Task 2: Fill in the table - Stages of problem solving by computer
| № | stage name | Description stage |
| Formulation of the problem | ||
| Mathematical model | ||
| Development of algorithm | ||
| Write an algorithm in a programming language | ||
| Debugging and testing of computer software | ||
| Analysis of the results. |
Task 3. Make assotsiogramm "Algorithm"
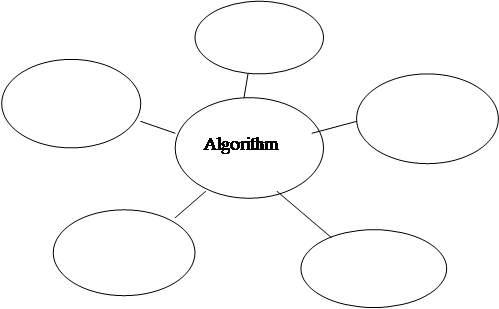 |
Task 4. Calculate the amount of paint to cover the floor in the gym. Create a mathematical model of the problem.
Methodology for setting 4.
Stages of solving the problem on a computer

1. Statement of the Problem
When painting the floor trying to paint cover the surface evenly. To perform this task is measured the length of the floor. This means that the amount of dye is proportional to the area that needs to be painted. Therefore, to solve the problem you need to know the floor area. It is essential assumption: the floor is rectangular in shape. To perform this task is measured the length, the width of the floor and compute its area. The real object - the floor of the hall - is engaged in a rectangle whose area is the product of the length by the width. When buying paint trying to find out how much area can be covered by the contents of one jar, and calculate the required number of cans.
2. The mathematical model
Let A - floor length, and - the width of the floor,S1 - An area which can be covered by the contents of one container, of N - number of cells, then:
floor area is calculated by the formula S=A×B, and the number of cells needed for painting the hall,N= A×B/S1.
Task 5. At a scientific seminar brought together scientists and shared with each other business cards. Total 210 business cards were distributed. How many scientists came to the seminar, it is known that there were not more than 20? Create a mathematical model of the problem
Tasks for the independent works
1. The members of the chess tournament after the next party exchanged handshakes with each other. Total played 210 games, then 210 times opponents shook hands. How many people participated in the tournament, when each played once with the rest and it is known that the participants did not have more than 38? Create a mathematical model of the problem.
2. Dana proper fraction whose denominator is 2 more than the numerator. If you take away from the numerator 1 and denominator to add 7 and reduce the fraction, then the result will be 1/2. Find the original fraction. (Use the table task №4, changing accordingly the formula in the cells).
3. Through the porthole of the ship is required to pull the sunken treasure chest. Will it be done?
4. 1) The area of a right triangle is equal to 6 cm. Find the length of the legs and the hypotenuse of the triangle, if one leg more than the other by 1 cm and it is known that the length of each of the parties does not exceed 12 cm.
Make a notebook in a mathematical model of this problem:
• select raw data;
• determine what is the result;
• Find the link between the source data and the result and write it in the form of mathematical relationships (present in the form of the equation).
5. 1) Repeat of formula side surface area and volume of a parallelepiped.
6. Requires obbit door 210h92 cm leatherette. Will pieces of leatherette 215h102 cm for door trim, if hem on each side is required by 2 cm of fabric?
7. It is necessary to paint the panel paint (walls) kitchen room. How many cans of paint is required, if the size of the kitchen: 405h310h285 cm, 88% of the wall takes tiles and 1 Bank of paint intended for painting an area of 5 m2?
Control questions:
1. What is mathematical modeling?
2. Define a mathematical model.
3. List the steps of solving a computer problem.
4. Describe the Euclidean algorithm
Practical work 2. Construction of algorithms
Objective: To study the properties of algorithms and methods for constructing algoritms.
Task 1: Fill in the table - Properties of algorithms:
| № | algorithm property | Characteristic properties |
| determinancy | ||
| mass character | ||
| Effectiveness | ||
| Readability | ||
| Finite | ||
| Correctness |
Task 2: Calculate the perimeter of any triangle on its three sides (the question of the existence of the triangle is not considered).
Methodology for the work 2:
Stage 1: Formulation of the problem.
Background: A, B, C - side of any triangle
Output: P - perimeter of the triangle.
Stage 2: A mathematical model.
P = A + B + C

Fig. 1. Example of a linear algorithm
Step 3: Preparation of the algorithm
Tasks for the independent excesses
Task 2. Create an algorithm for solving the problem with the help of verbal algorithm, flowcharts
1. Calculate the surface area and volume of a truncated cone by
following formulas 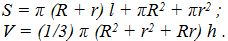
2. Calculate the coordinates of the center of gravity of the three particles with masses 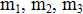 and the coordinates
and the coordinates
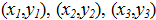 the formulas:
the formulas:
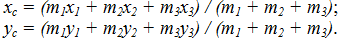
3. Calculate the area of a triangle with sides a, b, c by Heron's formula:
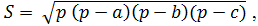
where p - semiperimeter, calculated by the formula (a + b + c) / 2.
4. Calculate the coordinates of the point that divides the segment 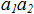 referring to
referring to 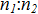 by the formulas:
by the formulas:

where 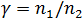 .
.
5. Calculate the medians of a triangle with sides a, b, c by the formulas: 
6. Calculate the area of a circle, and the circumference of the entered value of the radius.
7. Calculate the area S and perimeter L of the ellipse on the entered values of the semiaxes a and b:
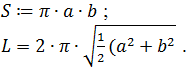
8. Calculate the volume V and the area of the lateral surface of the cylinder S on the input values of R and the height of the base radius of the cylinder H. 
9. Calculate the volume V and the lateral surface area of the cone S by entering values base radius r, height h and forming l:
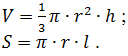
10. Calculate the volume V and surface area S of the sphere on the entered value of the radius r:

11. Given a four-digit number. With operations div and mod, find the sum of its digits.
12. Dan's side of an equilateral triangle. Find the area of this triangle, and the radii of the inscribed and circumscribed circles.
13. Given the coordinates of the three vertices of the triangle (x1, y1), (x2, y2), (x3, y3). Find the perimeter and area.
14. Dana circumference. Find area of a circle bounded by this circle.
15. The area of a circle is given. Find the length of the circle bounding the circle.
Technology of work
Не нашли, что искали? Воспользуйтесь поиском: