Задание 14. Дифференциальное и интегральное исчисление функций нескольких переменных.

14.1Найти область определения функции и изобразить ее:

14.2 Найти дифференциал функции в точке М(1; - 2)

14.3 Дана функция z = f(x;y). Найти: , , , , :z =

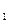14.4 Дана функция z = f(x;y), точка М(х ; y ) и вектор = {х ;у 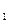}. Найти:

а) производную в точке М по направлению вектора ; б) grad z в точке М.

z = y² – x² + xy - 2x - 6y; М(2; 3) и вектор = {4;-3}.

14.5 Найти точки экстремума функции f(x) = - x² - 2xy - 3 y² - 4 x -4y + 3

14.6Составить уравнение касательной плоскости и нормали к поверхности в точке С(х ;y ;z ):

z = 2xy + 3y² – 5x; С(3;4;z )

Методические указания по выполнению контрольной работы.

Цель контрольной работы: закрепить теоретические знания для решения практических задач, рассмотреть вопросы, оставленные для самостоятельного изучения, приобрести практические навыки.

Работа выполняется в тетради от руки или на стандартных листах на компьютере.

При выполнении контрольной работы следует соблюдать следующие требования:

- указать номер варианта;

- в решении задач указывать формулы и их расшифровку;

- расчеты должны быть теоретически обоснованы, содержать пояснения и выводы;

- работа должна содержать титульный лист, задания, решение, заключение (ответ).

Вариант 7.

Не нашли, что искали? Воспользуйтесь поиском: