
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчет стойкости конструкции к механическим воздействиям
В процессе изготовления, транспортировки и эксплуатации ЭС подвергаются различным механическим воздействиям: линейным ускорениям, вибрации (периодическим знакопеременным нагрузкам) и ударам (непериодическим, кратковременным нагрузкам). Нагрузки могут быть направленными вдоль одной оси (линейные ускорения вдоль продольной оси при разгоне ракеты) либо действовать по всем трем взаимно перпендикулярным направлениям (наиболее общий случай).
ВГОСТ16019-2001 даны определения для стойкости, устойчивости и прочности аппаратуры при действии климатических и механических факторов (см. приложение А). Согласно этим определениям аппаратуру необходимо считать:
- вибропрочной, если она сохраняет работоспособность после воздействия механических нагрузок (например, после транспортировки к месту эксплуатации каким-либо видом транспорта, после выведения спутника на орбиту и т.д.);
- виброустойчивой, если она сохраняет работоспособность во время действия механических нагрузок (например, во время движения);
- вибростойкой, если она сохраняет работоспособность во время и после воздействия механических нагрузок.
Для вибростойкой аппаратуры при любых оговоренных в техническом задании внешних механических воздействиях должны выполняться следующие условия:
1. Если аппаратура установлена на амортизаторах, то нагрузка на каждый амортизатор не превышает допустимую величину для данного типа амортизатора и деформация амортизаторов во всем частотном диапазоне не превышает допустимый прогиб.
2. Усилия, возникающие в элементах крепления вследствие воздействия собственного веса блока или закрепленных элементов конструкции mg, линейного ускорения maли вибрационных ускорений (виброперегрузки) maв,не превышают величину, определяемую пределом прочности (пределом усталостной прочности при знакопеременных воздействиях) элементов крепления.
3. Прогибы печатных плат при вибрации не превышают допустимый прогиб, определяемый следующим образом:
 , (5.15)
, (5.15)
где l – размер меньшей стороны платы, м;
δдоп – допустимая стрела прогиба материала платы на базовой длине LБ = 1 м, определяемая по табл. 5.3.
4. Виброперегрузка и амплитуда колебаний электрорадиоэлементов не превышает значений, оговоренных в технических условиях на эти ЭРЭ.
5. При использовании микросборок с установленными на них бескорпусными компонентами амплитуда колебаний и виброскорость МСБ не должна превышать 0,3 мм и 800 мм/с соответственно.
Таблица 5.3
| Толщина листа, мм | Допустимая стрела прогиба на 1 м длины, мм/м2 | |||
| одностороннее фольгирование | двухстороннее фольгирование | |||
| гетинакс | стеклотекстолит | гетинакс | стеклотекстолит | |
| 0,8; 1,0 | ||||
| 1,5 | ||||
| 2,0 | ||||
| 2,5; 3,0 |
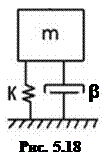 Механические воздействия передаются от объекта установки через амортизаторы или элементы жесткого крепления к корпусу блока (рис. 5.19,а), далее через элементы внутриблочной несущей конструкции (например, каркас) к точкам крепления ячеек, далее через несущее основание ячейки (печатную плату, металлическую рамку и т.д.) к местам крепления электрорадиоэлементов и микросборок. Вследствие значительной разницы массы и частоты собственных колебаний отдельных элементов конструкции блока приближенно можно считать, что передача колебаний на каждом из упомянутых участков описывается моделью колебательной системы с одной степенью свободы (рис. 5.18).
Механические воздействия передаются от объекта установки через амортизаторы или элементы жесткого крепления к корпусу блока (рис. 5.19,а), далее через элементы внутриблочной несущей конструкции (например, каркас) к точкам крепления ячеек, далее через несущее основание ячейки (печатную плату, металлическую рамку и т.д.) к местам крепления электрорадиоэлементов и микросборок. Вследствие значительной разницы массы и частоты собственных колебаний отдельных элементов конструкции блока приближенно можно считать, что передача колебаний на каждом из упомянутых участков описывается моделью колебательной системы с одной степенью свободы (рис. 5.18).
 |
Рис. 5.19
В том случае, когда блок установлен на амортизаторах (рис. 5.19, б), должны быть выполнены условия рациональной расстановки амортизаторов:
ΣPi=G; ΣPi∙xi=0; ΣPi∙yi=0; ΣPi∙zi=0;
ΣPi∙xi∙yi=0; ΣPi∙yi∙zi=0; ΣPi∙xi∙zi=0, (5.16)
где G = mg – вес блока;
Pi– нагрузка, приходящаяся на i-й амортизатор (реакция амортизатора);
xi, yi, zi– координаты i-го амортизатора (начало координат выбирается произвольно, но часто удобно принять за начало отсчета центр масс блока).
Амплитуда колебаний блока, установленного на амортизаторах, для любой частоты внешнего гармонического вибрационного воздействия определяется из решения дифференциального уравнения колебательной системы с одной степенью свободы (рис. 5.18):
 , (5.17)
, (5.17)
где S0, S1– амплитуды колебаний объекта установки и корпуса блока;
a0, a1 – вибрационные ускорения объекта установки и корпуса блока;
η – коэффициент передачи;
 – собственная частота колебаний блока на амортизаторах, Гц;
– собственная частота колебаний блока на амортизаторах, Гц;
 – суммарная жесткость системы амортизаторов вдоль оси, параллельной направлению колебаний, Н/м;
– суммарная жесткость системы амортизаторов вдоль оси, параллельной направлению колебаний, Н/м;
δ0 – коэффициент демпфирования амортизаторов.
Поскольку упругий элемент амортизатора испытывает деформацию, что может привести к отказу, необходимо знать амплитуду этой деформации (прогиба):
 . (5.18)
. (5.18)
Амплитуда деформации на любой частоте не должна превышать величину допустимого прогиба для конкретного типа амортизатора.
Справочные данные по различным типам серийно выпускаемых амортизаторов приведены в [20].
Графики зависимостей η и η* от относительной частоты f/f0приведены на рис. 5.20 и 5.21. Наибольшая амплитуда колебаний блока и амплитуда деформации упругого элемента при постоянной амплитуде колебаний объекта установки наблюдается на частоте близкой к частоте собственных колебаний (явление резонанса). Поэтому проверку допустимой величины амплитуды колебаний и виброускорений (виброперегрузок) следует проводить на частоте резонанса, если она попадает в диапазон частот внешних вибраций, а также на крайних верхней и нижней частотах внешних вибраций.
Поскольку механические колебаний объекта установки могут происходить в любом из направлений (если иное не оговорено в техническом задании), а у амортизаторов продольная и поперечная жесткости, как правило, не совпадают, а следовательно, не совпадают частоты собственных колебаний вдоль разных осей, проверку вибростойкости необходимо в общем случае производить вдоль каждой оси отдельно.
В случае жесткого закрепления блока или микроблока на объекте его колебания передаются корпусу блока без изменений:
S1= S0; a1= a0.
Различные варианты передачи вибрации от корпуса блока к точкам крепления ячеек представлены на рис. 5.19, в-ж.
 |
Рис. 5.20 Рис. 5.21
Если колебания корпуса (в данном примере вдоль вертикальной оси) передаются вдоль ребер или стенок каркаса (рис. 5.19, в), то ввиду значительной продольной жесткости несущих элементов каркаса можно считать, что колебания к точкам крепления ячеек передаются без изменений: S2= S1; a2= a1.
Если вибрация передается перпендикулярно ребрам каркаса (рис. 5.19, г), то для такой конструкции применима модель в виде балки, нагруженной по длине сосредоточенными массами ячеек mi(рис. 5.22, а, б). Колебания такой системы также описываются моделью с одной степенью свободы (см. рис. 5.18), а значения коэффициентов передачи  и
и  вычисляются по формулам (5.17) и (5.18). Частота собственных колебаний определяется
вычисляются по формулам (5.17) и (5.18). Частота собственных колебаний определяется
 , Гц, (5.19)
, Гц, (5.19)
где E – модуль упругости материала балки, Н/м2;
J – момент инерции сечения балки, м4;
ml– распределенная масса балки, кг/м (рис. 5.22, в);
а – длина балки (расстояние между опорами), м;
 φ – коэффициент, зависящий от способа закрепления концов балки (табл. 5.4).
φ – коэффициент, зависящий от способа закрепления концов балки (табл. 5.4).
Рис. 5.22
Таблица 5.4
| Коэффициент частоты φ | ||||
| Способ закрепления | Номер гармоники | |||

| 3,56 | 9,82 | 19,3 | 31,9 |
| 2,45 | 7,95 | 16,6 | 28,4 | |
| 1,57 | 6,3 | 14,1 | 24,2 | |
| 0,56 | 3,5 | 9,83 | 19,3 |
Приведение набора п одинаковых равномерно распределенных по длине масс ячеек ml к эквивалентной распределенной массе выполняется по формуле
 , кг/м. (5.20)
, кг/м. (5.20)
Приведение неравных или неравномерно расположенных масс описано в [2].
 Для конструкции, изображенной на рис. 5.19, д, например, микроблока пенальной конструкции с микросборками, прикрепленными ко дну корпуса, характерна передача колебаний блока к микросборкам через упругость стенки блока. В этом случае применяется модель в виде пластины, закрепленной по периметру и нагруженной по площади массами ЭРЭ и микросборок (рис. 5.23). Колебания пластины вдоль оси, перпендикулярной плоскости пластины, также описываются моделью рис. 5.18 и выражениями (5.17) и (5.18), при этом
Для конструкции, изображенной на рис. 5.19, д, например, микроблока пенальной конструкции с микросборками, прикрепленными ко дну корпуса, характерна передача колебаний блока к микросборкам через упругость стенки блока. В этом случае применяется модель в виде пластины, закрепленной по периметру и нагруженной по площади массами ЭРЭ и микросборок (рис. 5.23). Колебания пластины вдоль оси, перпендикулярной плоскости пластины, также описываются моделью рис. 5.18 и выражениями (5.17) и (5.18), при этом
 , Гц, (5.21)
, Гц, (5.21)
где a, b – размеры пластины, м;
mпл, mэрэ – масса пластины и суммарная масса ЭРЭ, МСБ, кг;.
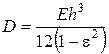 – цилиндрическая жесткость пластины, Н∙м;
– цилиндрическая жесткость пластины, Н∙м;
E – модуль упругости, Н/м2;
ε – коэффициент Пуансона материала пластины (приложение Ж);
 – коэффициент, зависящий от формы пластины и условий закрепления на сторонах, значения p, q и r определяются по табл. 5.5.
– коэффициент, зависящий от формы пластины и условий закрепления на сторонах, значения p, q и r определяются по табл. 5.5.
При расчете амплитуды колебаний, передаваемых от точек крепления ячеек к электрорадиоэлементам или микросборкам, применима модель в виде нагруженной пластины (рис. 5.23). Расчет амплитуды колебаний и виброперегрузок зависит от направления колебаний. Если линия колебаний направлена вдоль плоскости ячейки (см. рис. 5.19, е), то ввиду значительной продольной жесткости печатной платы, рамки и т.д. колебания передаются почти без изменений: S3=S2; a3=a2(рис 5.19, е). При колебаниях, перпендикулярных плоскости ячейки (рис. 5.19, ж), расчет ведут, как для случая, представленного на рис. 5.16, д. При этом  и
и  определяют по (5.17) и (5.18), f0по (5.21); допустимый прогиб
определяют по (5.17) и (5.18), f0по (5.21); допустимый прогиб  по (5.15).
по (5.15).
Таблица 5.5
| Эскиз закрепления | Коэффициенты α | Эскиз закрепления | Коэффициенты α | ||||
| p | q | r | p | q | r | ||

| 
| 0,43 | |||||
| 2,32 | 2,44 | 0,12 | 0,75 | 5,14 | |||
| 2,57 | 5,14 | 0,12 | 0,31 | 0,12 | |||
| 2,44 | 2,71 | 2,44 | 5,14 | ||||
| 5,14 | 2,93 | 2,42 | 0,12 | ||||
| 5,14 | 3,13 | 5,14 | 2,44 | ||||
| 0,13 | 0,12 | 0,707 | 2,44 | ||||
| 0,12 | 0,2 | ||||||
| 0,514 | 5,14 | ||||||
| 0,83 | 2,44 |
Для ячейки на печатных платах размеры пластины принимаются равными размерам печатной платы. При определении условий закрепления краев можно руководствоваться следующими правилами (рис. 5.24):
· защемление края (в табл. 5.5 обозначено наклонной штриховкой) обеспечивается, если край платы приклеен, приклепан или привинчен в нескольких точках по длине к жесткой рамке или планке, также жестко закрепленной на каркасе блока; если на краю платы закреплен разъемный соединитель с большим числом контактов, который при установке ячейки в блок сочленяется с жестко закрепленной ответной частью соединителя;
· опирание края (обозначено штриховой линией) обеспечивается, если край платы скользит вдоль направляющей в каркасе; если край платы прикреплен к нежесткой (например, тонкостенной) или нежестко закрепляемой на каркасе планке или угольнику (в этом случае край платы не может смещаться перпендикулярно плоскости платы, но может поворачиваться);
· жесткое закрепление в точках (обозначено крестиками) будет в случае сборки пакета ячеек на стойках, шпильках.
Для ячеек сложной формы или состоящих из неоднородных материалов (цифровые ячейки 4 поколения, печатные платы с рамками или металлическими планками, микроблоки пенального типа и т.д.) расчет ведется по формуле (5.21) за исключением способа определения цилиндрической жесткости. Для примера на рис. 5.25 представлена ячейка на металлической рамке с наиболее слабым сечением при изгибе А-А, для которого и ведется расчет. В данном случае жесткость ячейки складывается из жесткости печатной платы (5.21) и жесткости рамки:
D = Dпл+ Dр, Н∙м. (5.22)

| 
|
| Рис. 5.24 | Рис. 5.25 |
Для определения цилиндрической жесткости рамки необходимо найти момент инерции сечения рамки:
 , Н∙м. (5.23)
, Н∙м. (5.23)
Чтобы рассчитать Jр,необходимо разбить сечение рамки на простейшие фигуры. В данном примере сечение разбито на четыре прямоугольника, момент инерции каждого из которых определяется по формуле
 , м4, (5.24)
, м4, (5.24)
где hi– размер прямоугольника вдоль оси z;
bi– размер вдоль оси у.
Далее необходимо определить координаты ziцентров прямоугольников и координату центра тяжести всего сечения z0:
 , м. (5.25)
, м. (5.25)
После этого находят Jрдля подстановки в (5.23), (5.22), (5.21):
 . (5.26)
. (5.26)
Моменты инерции сечений других элементов конструкции, например, корпуса аналогового микроблока пенального типа и т.п., находят аналогично.
Коэффициент демпфирования δ0в формулах (5.17), (5.18) зависит от материала упругого элемента (см. приложения Ж) либо определяется экспериментально для сложных конструкций. При δ0<<1 максимальное значение коэффициента передачи, наблюдаемое при резонансе, приблизительно рассчитывают по формуле
 . (5.27)
. (5.27)
Для типичных конструкций известны ориентировочные значения ηр: для микроблоков СВЧ пенального типа – около 40, для цифровых ячеек на металлических рамках – 10...25, для ячеек на платах из стеклотекстолита – 5...12.
Исходными данными для анализа стойкости блока к вибрациям являются диапазон частот и амплитуда (ускорение, перегрузка) вибраций, действующих на объекте установки блока (задается в техническом задании).
Анализ стойкости блока к вибрациям выполняется в следующем порядке.
1. Выявить в конструкции блока элементы, чувствительные к воздействию нагрузок, и определить допустимую для них интенсивность вибрации. Как правило, такими элементами являются электрорадиоэлементы, амортизаторы (допустимые нагрузки для них приведены в ТУ, справочных данных), печатные платы (допустимый прогиб для которых находят по формуле (5.15)), микросборки с бескорпусными компонентами и т.д.
2. Построить аналогично рис. 5.19 модель последовательной передачи колебаний к внутренним элементам блока. Пользуясь формулами (5.17)…(5.26), рассчитать для каждого из передаточных звеньев частоты собственных колебаний. Расчет выполнить для всех возможных направлений вибрации.
3. Если блок установлен на амортизаторах, проверить условие их рациональной расстановки (5.16).
4. Последовательно рассчитать амплитуды колебаний (ускорения, перегрузки, амплитуды деформации) для всех промежуточных звеньев (рис. 5.19,б-ж) вплоть до ЭРЭ, МСБ. Расчет выполнить для всех возможных направлений вибрации и на всех частотах собственных колебаний передаточных звеньев, попадающих в диапазон частот внешних вибраций, а также на граничных частотах диапазона (поддиапазонов) внешних вибраций. При необходимости взаимный перевод амплитуды вибрации S, виброскорости V, ускорения a и перегрузки n на любой частоте выполняется по формулам:
V = 2π∙f∙S; a = 2 π∙f∙V = (2π∙f)2∙S; n = a/g, (5.28)
где g = 9,83 м/с2– ускорение свободного падения.
5. Проверить выполнение условий виброустойчивости 1…5 для всех критичных элементов конструкции и в случае нарушения хотя бы одного из них изменить конструкцию блока (увеличить жесткость несущих конструкций блока и ячеек, применить дополнительную виброизоляцию, выбрать более вибропрочные элементы и т.д.), после чего проверку повторить.
Расчет надежности
В пояснительной записке ВКР выполняется расчет и анализ показателей надежности (ПН), требования к которым приведены в техническом задании. По своему составу ПН бывают единичными и комплексными. В табл. 5.6 приведены основные единичные показатели надежности.
Табл. 5.6
| Характеризуемое свойство надежности | Наименование показателя | Обозначение |
| Безотказность | Вероятность безотказной работы в пределах заданной наработки t | P(t) |
| Интенсивность отказов | λ (t) | |
| Средняя наработка до отказа | T ср | |
| Средняя наработка на отказ | T 0 | |
| Гамма-процентная наработка до отказа | Tγ | |
| Ремонтопригодность | Среднее время восстановления работоспособного состояния | Тв |
| Вероятность восстановления работоспособного состояния за время t | Pв(t) | |
| Долговечность | Средний ресурс | Тр |
| Гамма-процентный ресурс | Трγ | |
| Средний срок службы | Т сл | |
| Гамма-процентный срок службы | Т сл γ | |
| Сохраняемость | Средний срок сохраняемости | Тс |
| Гамма-процентный срок сохраняемости | Тсγ |
В отличие от единичного показателя комплексный показатель надежности количественно характеризует не менее двух свойств, составляющих надежность, например безотказность и ремонтопригодность. Определения единичных и комплексных показателей надежности даны в ГОСТ 27.002-89.
Методы расчета надежности по внезапным отказам при последовательном соединении элементов в зависимости от полноты учета факторов, влияющих на работу изделия, делят на прикидочный, ориентировочный и уточненный методы [17]. В конструкторских и технологических ВКР чаще всего используется уточненный метод расчета при допущении, что интенсивности отказов всех радиоэлементов постоянны. В исследовательских работах методика расчета надежности зависит от основных целей всей работы и согласовывается с руководителем и консультантом проекта.
Для выполнения уточненного расчета необходима исходная информация:
– электрическая принципиальная схема изделия;
– справочные данные о показателях надежности электрорадиоэлементов;
– сведения об условиях эксплуатации и режимах нагружения элементов.
Расчет состоит в определении основных показателей, характеризующих безотказность электронного средства: наработки на отказ Т 0 и вероятности безотказной работы Р (t). Методика его выполнения приведена в [17], в которой можно выделить следующие этапы.
1. Все радиоэлементы проектируемого изделия разбивают на отдельные группы, каждая из которых содержит РЭ одного вида (резисторы, конденсаторы, транзисторы и др.). Число элементов в каждой группе – Ni.
2. Для всех РЭ определяют коэффициенты электрической нагрузки К н по формуле, которую в общем виде можно представить:
 , (5.29)
, (5.29)
где Эр и Эдоп – реальное и допустимое значение электрического параметра.
Реальное значение электрического параметра находится путем электрического расчета заданной схемы, а допустимое значение Эдоп берется в справочно-нормативной литературе для выбранных типов РЭ. Справочно-методический материал по расчету  приведен в [17].
приведен в [17].
3. По справочным данным [17] находят базовые величины интенсивностей отказов λб.
4. Для каждого вида РЭ определяют эксплуатационную интенсивность отказов λЭ i . Расчеты производятся по математическим моделям, приведенным в приложениях [17]. Например, эксплуатационная интенсивность отказов интегральных микросхем определяется по формуле
 ,
,
где λб – базовая интенсивность отказов интегральных схем,
К с.т – коэффициент режима, который зависит от сложности интегральных схем и температуры окружающей среды (табл. П1.5);
К корп – коэффициент, учитывающий зависимость λэ от корпуса интегральных схем (К корп=3 для пластмассовых корпусов и К корп=1 - для всех остальных);
К v – коэффициент, учитывающий зависимость λэ от максимальных значений напряжения питания (табл. П1.6);
К э – коэффициент, учитывающий условия эксплуатации изделия (Прил. 1.1);
λб - базовая интенсивность отказов интегральных схем (табл. П1.4).
5. Определяют общую интенсивность отказов РЭ в изделии  путем суммирования произведений
путем суммирования произведений  по всем группам (видам элементов) по формуле
по всем группам (видам элементов) по формуле
 .
.
6. Рассчитывают показатели надежности по формулам
 ,
,  .
.
В заключительной части расчета выполняется анализ полученных результатов.
Для расчета надежности сложного изделия рекомендуется использовать отечественные программные средства, например, АСОНИКА-Б [17, 18].
Не нашли, что искали? Воспользуйтесь поиском: