
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение функции в GPSS
Лабораторная работа 4.
Переменные и функции
Переменные
Общая характеристика переменных. При построении модели системы, иногда возникает необходимость задать сложные математические или логические соотношения между атрибутами системы. Для этой цели в программе используются переменные.
В GPSS имеется три типа переменных:
1) арифметические переменные;
2) арифметические переменные c «плавающей точкой»;
3) булевы переменные.
Значение арифметических переменных может использоваться как:
1) операнд блока; в этом случае значение арифметической переменной может представлять собой:
– номер объекта (устройства, МКУ, очереди и т. п.);
– номер параметра транзакта;
– значение стандартного числового атрибута;
3) операнд А функции;
4) операнд А таблицы;
5) операнд выражения другой переменной.
В выражениях арифметические переменные используют такие арифметические операции:
+ алгебраическое сложение;
– алгебраическое вычитание;
# алгебраическое умножение;
/ алгебраическое деление (результатом операции является целая часть частного);
@ деление по модулю;
^ возведение в степень;
\ деление без остатка (перед делением у обоих операндов отбрасываются дробные части, результатом операции есть целая часть частного).
Привычно используемый для умножения во многих языках знак «*», зарезервирован в GPSS для обозначения косвенной адресации, однако в GPSS World есть возможность в меню настройки параметров переопределить для умножения знак «*», А для косвенной адресации – «#». Косвенная адресация является мощным средством для построения компактных и гибких моделей. Ее идея заключается в том, что можно обратиться к любому объекту или СЧА через параметры транзактов. Доступ же к параметрам транзактов осуществляется через СЧА P j, где j – номер параметра транзакта (например, 10) или Р$имя, где имя – имя (идентификатор) параметра транзакта. Так как обращение к объекту возможно только через параметр транзакта, то символ P может опускаться. Например, выражение Q*7 или Q*P7 определяет текущее значение длины очереди, номер которой задан в параметре 7 транзакта. Если в седьмом параметре хранится значение 3, то это будет текущее значение длины очереди c номером 3.
В выражениях может быть задано любое число приведенных операций в различных комбинациях. Знак результата вычисляется по обычным алгебраическим правилам. Допускаются отрицательные значения переменных. Выражения анализируются слева направо. Возведение в степень, умножение, деление и деление по модулю выполняются раньше, чем сложение и вычитание.
Вычисленное значение переменной является ее стандартным числовым атрибутом.
Арифметические переменные. Арифметические переменные аналогичны арифметическим выражениям в алгоритмических языках. Переменная задается оператором VARIABLE, называемым оператором описания переменной, который содержит арифметическое выражение. Формат оператора описания переменной:
Таблица 19
| Поле | Информация, задаваемая в поле |
| Метка | Имя (числовое или символьное) переменной |
| Операция | VARIABLE |
| ОперандА | Выражение, которое используется для вычисления значения переменной |
При обращении к переменной используется обозначение V<номер переменной> или V$<имя переменной>, т.е. V – это СЧА переменной.
Пример 16
Оператор описания VARIABLE определяет арифметическую переменную RSL:
RSL VARIABLE QT$WAITL+3-FN$DSTRB#P7
При любом обращении к переменной RSL (употребляется обозначение V$RSL) ее значение вычисляется как текущая длина очереди WAlTL (QT$WAITL – СЧА регистратора очереди) плюс константа 3 и минус произведение значения функции DSTRB на значение параметра 7 транзакта, обрабатываемого в данный момент. В приведенном выражении FN – СЧА для обращения к функции, a P – СЧА транзакта.
Перед выполнением любой арифметической операции определяется значение каждого элемента и выделяется его целая часть. Постоянные без знака считаются положительными числами.
В выражении арифметической переменной могут быть использованы любые СЧА, функции и другие арифметические переменные. Запрещается использование самой вычисляемой переменной, А также переменных со знаком, так как знаки в данном случае рассматриваются как арифметические операции.
Система моделирования GPSS допускает использование скобок в выражениях арифметических переменных (для группировки членов или для обозначения операции умножения).
В GPSS World выражения, записанные в круглых скобках, обрабатываются вычислительной процедурой встроенного алгоритмического языка PLUS. Поэтому их можно использовать в качестве операндов блоков и операторов языка GPSS. Например, выражение, описанное в примере 16, может быть использовано таким образом:
ADVANCE (QT$WAITL+3-FN$DSTRB#P7)
1.B GPSS/PC выражение может содержать не больше пяти пар скобок (не считая скобок, используемых при описании элементов матриц).
2. Пробелы между символами в выражениях не допускаются. Левый пробел записи считается концом выражения. Для записи выражения, превышающего длину строки, можно ввести другой оператор VARIABLE c именем, отличным от имени первой переменной, и включить значение новой переменной в качестве одного из операндов в выражение первой арифметической переменной.
Пример 17
ADD VARIABLE P10+25
При обращении к арифметической переменной ADD ее значение вычисляется как сумма значений десятого параметра транзакта, обрабатываемого в данный момент, и константы 25.
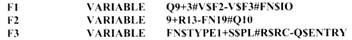
Выражение для F1 содержит как операнды переменные F2 и F3.
PROFIT VARIABLE V*P*FN*P2
Переменная PROFIT будет вычислена следующим образом. Вначале определяется значение второго параметра текущего транзакта. Пусть в параметре P2 хранится значение 3. Затем вычисляется значение функции 3. Пусть оно равно 10. После этого определяется значение параметра c номером 10. Пусть содержимым этого параметра будет число 5. Тогда переменной PROFIT присваивается значение переменной 5.
COMP VARIABLE X*P4/100
При обращении к арифметической переменной COMP ее значение вычисляется как частное от деления значения сохраняемой величины (СЧА X), номер которой определяется четвертым параметром транзакта, обрабатываемого в данный момент, на константу 100. Сохраняемые величины позволяют хранить значения глобальных переменных, доступных из любой части модели. Такой прием используется для выделения старших разрядов чисел. Например, пусть в четвертом параметре текущего транзакта записано число 6. И пусть в сохраняемой величине 6 хранится число 12345. При обращении к переменной COMP происходит следующее:
1) определение значения параметра 4 (получаем число 6);
2)определение значения 12345, которое хранится в ячейке X*P4, т.е. в ячейке 6;
З)значение 12345 делится на 100 (c отбрасыванием остатка), в результате получается 123.
Арифметические переменные c плавающей точкой аналогичны рассмотренным арифметическим переменным, за исключением того, что все операции над операндами выражений переменных c плавающей точкой выполняются без преобразования операндов и промежуточных результатов в целые значения. Лишь окончательный результат вычисления преобразуется в целое число.
Формат операторов описания арифметических переменных c плавающей точкой идентичен рассмотренному выше формату операндов описания арифметических переменных за исключением того, что в поле операции записывается слово FVARIABLE. Правила написания операторов те же, что и для арифметических переменных. Арифметическая переменная и переменная c плавающей точкой не могут иметь одинаковые номера. Если они имеют одинаковые номера, то при вычислении используется более позднее из двух описаний.
Различие результатов, полученных при вычислении c плавающей точкой и фиксированной, можно увидеть из такого примера:
FLOAT FVARIABLE 10#(ll/3)
FIXED VARIABLE 10#(ll/3)
Значение переменной FLOAT равно 36, так как константа 10 умножается на 3,67 и от результата 36,7 взята целая часть. Переменная FIXED равна 30, так как результат промежуточной операции деления будет округлен до 3.
1. Для переменных c плавающей точкой не допускается операция деления по модулю.
2. Использование дробных констант допускается только при описании переменных c плавающей точкой.
З.Стандартный числовой атрибут V$<имя переменной> используется для обращения к значениям как арифметических переменных, так и переменных c плавающей точкой. Способ вычисления переменной определяется оператором описания этой переменной.
Булевы переменные. Булевы переменные позволяют принимать решения в зависимости от значений СЧА и состояния объектов GPSS, используя для этого только одно выражение.
Булевы переменные – это логические выражения, состоящие из различных СЧА и (или) других булевых переменных. В булевой переменной проверяется одно или несколько логических условий. Результатом проверки есть единица (истина), если условия выполняются, и ноль (ложь) – в противном случае.
При описании булевых переменных используются три типа операторов: логические, булевы и операторы отношений.
Логические операторы связаны c такими ресурсами, как устройства, МКУ и логические ключи. Они используются для определения состояния данных объектов. Логические операторы, используемые в GPSS, представлены в табл. 20
Таблица 20
| Логические операторы | Значение оператора, отражающее состояние ресурса |
| FVj или Fj | Равно 1, если устройство j занято или обслуживает прерывание, в противном случае – 0 |
| FNVj | Равно 1, если устройство j не занято и не обслуживает прерывание, в противном случае – 0 |
| Ij | Равно 1, если устройство j обслуживает прерывание, в противном случае – 0 |
| NIj | Равно 1, если устройство j не обслуживает прерывание, иначе – 0 |
| NUj | Равно 1, если устройство j не используется, в противном случае – 0 |
| UJ | Равно 1, если устройство j используется, в противном случае – 0 |
| SFJ | Равно 1, если многоканальное устройство у заполнено, иначе – 0 |
| SNFj | Равно 1, если МКУ j не заполнено, иначе – 0 |
| SEj | Равно 1, если МКУ j пусто, иначе – 0 |
| SNEj | Равно 1, если МКУ j не пусто, иначе – 0 |
| SVj | Равно 1, если МКУ j находится в состоянии использования, в противном случае – 0 |
| SNVJ | Равно 1, если МКУ j не используется, в противном случае – 0 |
| LRj | Равно 1, если логический ключ j выключен, иначе – 0 |
| LSj | Равно 1, если логический ключ j включен, иначе – 0 |
Операторы отношения выполняют алгебраическое сравнение операндов. Операндами могут быть константы или стандартные числовые атрибуты. Все операторы отношений записываются в кавычках:
"G" (G reater) – больше;
"L" (L ess) – меньше;
"E" (E qual) – равно;
"NE" (N ot E qual) – не равно;
"LE" (L ess than or E qual) – меньше или равно;
"GE" (G reater than or E qual) – больше или равно;
Есть два булевых оператора: "OR" – оператор «или», и " AND " – оператор «и». Оператор «или» проверяет, выполняется ли хотя бы одно из проверяемых условий. Оператор «и» требует выполнения обоих условий.
Определение функции в GPSS
В GPSS рассматриваются пять типов функций:
1) дискретная числовая (D),
2) непрерывная числовая (C),
3) табличная числовая (L),
4) дискретная атрибутивная (E),
5) табличная атрибутивная (M). Рассмотрим два первых типа функций.
Дискретная функция представляет собой кусочно-постоянную функцию, которая состоит из горизонтальных ступеней (рис. 2). Непрерывная функция представляет собой кусочно-непрерывную функцию. Непрерывная функция в GPSS состоит из соединенных между собой прямых отрезков и представляет собой ломаную линию (рис. 3). Чтобы задать дискретную функцию, необходимо задать координаты крайних правых точек горизонтальных отрезков. Для непрерывной функции необходимо задать координаты всех точек, которые являются концами отрезков.
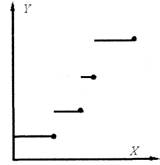
Рис. 2

Рис. 3
Действия, необходимые для определения дискретной и непрерывной GPSS-функции:
1.Присвоить функции имя. Имя может быть числовым либо символьным.
2. Задать аргумент функции. Аргументом могут быть:
1) ссылка на генератор случайных чисел, используемый для розыгрыша в соответствии c распределением, заданным функцией;
2) стандартный числовой атрибут;
3) ссылка на любую другую функцию.
В первом случае аргумент задается в виде RNj, j – целое число (номер генератора). В GPSS/PC j = 1,..., 7, т.е. возможно обращение к семи идентичным генераторам случайных чисел. При этом генераторы выдают случайные числа в диапазоне 0... 0,999. В GPSS World количество генераторов случайных чисел неограниченно, А выдаваемые ими значения 0... 0,999999.
3. Задать тип функции и число крайних точек функции.
4. Задать значения аргумента (переменной) и соответствующие значения функции (т.е. координаты крайних точек функции).
Три первых элемента информации указываются в операторе определения функции. Формат оператора представлен в таблице.
Таблица 21
| Поле | Информация, задаваемая в поле |
| Метка | Имя функции (числовое или символьное) |
| Операция | FUNCTION |
| Операнды А В | RNJ О = 1,..., 7) или СЧА. Dn либо Сn, где D определяет дискретную функцию, С определяет непрерывную функцию; n – для дискретной функции – это число различных значений, получаемых функцией (количество горизонтальных отрезков), для непрерывной функции – это число, на единицу больше числа отрезков, составляющих функцию (количество точек) |
За каждым оператором описания FUNCTION следуют операторы задания координат точек функции (значений аргументов Xi и соответствующих им значений функции Yi) – это операторы описания координат функции. Их формат:
1) если координаты всех точек расположены в одной строке оператора описания функции:
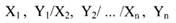
2) если координаты точек расположены в нескольких операторах описания функции:
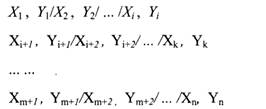
где Xi и Yi – координаты i -й точки функции (в случае моделирования случайной величины Xi является i -й суммарной (кумулятивной) частотой, Yi – соответствующим значением случайной величины).
Особенности оператора описания координат функции:
1) основной единицей информации оператора описания координат функции является пара значений Xi, Yi (координаты точки i);
2) значения координат Xi и Yi – одной точки функции разделяются запятой;
3) последовательные наборы координат разделяются знаком «/»;
4) координаты Xi и Yi – относящиеся к одной точке, задаются одним оператором, т.е. пара координат одной точки не должна разрываться;
5) все строки описания координат функции должны начинаться c первой позиции;
6) во всех случаях значения аргумента должны удовлетворять следующим неравенствам:
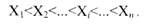
Значение функции является ее стандартным числовым атрибутом. Способ ссылки на этот атрибут зависит от того, как задано имя функции: в символьном или числовом виде. Если имя числовое, то к значению функции обращаемся через FNj (где j – номер функции), если имя символьное – через FN$<имя функции>.
1. Аргументом функции может быть и значение какой-либо другой функции.
2. Каждая функция должна иметь, по крайней мере, две описанные точки.
Пример 18
Пусть необходимо смоделировать дискретную случайную переменную, заданную в табл. 22.
Таблица 22
| Значение случайной переменной | Относительная частота | Суммарная частота | Диапазон | Интер-вал |
| 2 | 0,15 | 0,15 | [0,0-0,15] | |
| 0,20 | 0,35 | (0,15-0,35] | ||
| 0,25 | 0,60 | (0,35 – 0,60] | ||
| 0,22 | 0,82 | (0,60 – 0,82] | ||
| 0,18 | 1,00 | (0,82 – 1,0] |
GPSS-функцию можно определить таким образом:
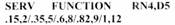
Графическая интерпретация функции показана на рис. 4.

Рис. 4
Особенности вычисления дискретных и непрерывных GPSS-функций:
1. В начальной фазе выполняемые действия при вычислении дискретной и непрерывной функции одинаковы. При обращении к функции определяется значение ее аргумента. Потом просматривается упорядоченный ряд значений Х1<Х2<...<Хi<...<Хп для определения интервала, в который попало значение аргумента (пусть это будет интервал между точками i – 1 и i).
2. Если функция дискретная, то второй элемент соответствующей пары Xi, Yj является значением функции. Если функция непрерывная, выполняется линейная интерполяция для пары точек i – 1 и i, находящихся на краях интервала значений функции, на который указало значение аргумента. Целая часть результата интерполяции и является значением функции.
3. Если значение аргумента функции больше значения координаты Хn последней точки, то в обоих случаях (дискретной и непрерывной функции) значениями функции являются значения Yn.
Пример 19
Моделирование случайной переменной, равномерно распределенной на интервале [2,5].
Эта случайная переменная может быть смоделирована функцией:
Не нашли, что искали? Воспользуйтесь поиском: