
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
INN FUNCTION RN2,C2
0,2/1,6
Графическая интерпретация непрерывной функции показана на рис. 5.
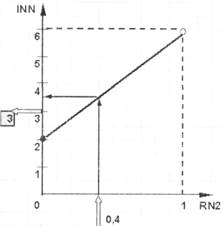
Рис.5
Так как максимальное значение, которое может выдать генератор случайных чисел, равно 0,999, то фактические значения интервалов времени распределены равномерно на интервале [2, 5] и равны, соответственно, одному из значений: 2, 3, 4, 5. Если генератор выдаст число 0,999, функция, которая показана на рис. 5, примет значение 5,996, целая часть которого равна 5 (это и будет значением GPSS-функции INN). В случае, если генератор случайных чисел RN2 выдаст значение 0,4, GPSS-функция INN примет значение 3 (см, рис. 5).
GPSS-функция INN не может принять значение, равное 6 (несмотря на то, что второй элемент второй пары оператора описания координат функции 0,2/1,6 равен 6).
Точные граничные значения RN2, соответствующие возможным значениям функции INN, представлены в табл. 23.
Таблица 23
| Целая часть значения функции | Диапазон значений RN2 |
| 2 | [0,0 – 0,25] |
| (0,25 – 0,50] | |
| (0,50 – 0,75] | |
| (0,75 – 0,999] |
Равномерное распределение [2, 3, 4, 5] не может быть задано непосредственно c помощью операндов А и В блока GENERATE. Здесь имеем четыре возможных значения, тогда как интервал А ± В (А и В целые) всегда имеет нечетное число элементов.
Пример 20
Часто возникают ситуации, когда в процессе моделирования необходимо переходить в различные блоки программы в зависимости от логики работы модели. Стандартные блоки GPSS WORLD такие, как TEST (см. параграф 16) и TRANSFER, не всегда могут решить эту проблему, так как они позволяют распределять транзакты максимум по двум направлениям. В случае, когда осуществляется условный переход на одну из нескольких меток (если более двух, то в обычных языках программирования используется оператор CASE OF), необходимо построить переключающую функцию. Для вызова переключающей функции используется блок TRANSFER в режиме безусловного перехода.
Пример переключающей функции:


Переключающая функция построена на основе дискретной функции c тем отличием, что результатом функции являются метки. В этом примере переход осуществляется к одной из меток в зависимости от числа, которое получаем от генератора случайных чисел.
Моделирование неравномерных случайных величин. Использование функций в блоках GENERATE и ADVANCE. Пусть распределение интервалов поступления через определенный блок GENERATE или время задержки в некотором блоке ADVANCE не является равномерным (либо является равномерным c «плавающими во времени», т.е. нефиксированными значениями среднего и половины поля допуска). Для входов транзактов в модель через этот блок GENERATE и для задания закона времени задержки в соответствующем блоке ADVANCE необходимо использовать функции и (или) СЧА. Использование функций, заданных в операндах блоков, зависит от контекста. От значения функции берется целая часть, за исключением тех случаев, когда это значение используется в качестве операнда В блоков GENERATE и ADVANCE или операнда C блока ASSIGN. В табл. 24 показаны различные варианты использования функций и СЧА в качестве операндов А и В блоков GENERATE и ADVANCE. Под результатом понимается значение интервала поступления или задержки.
Таблица 24
| Операнд А | Операнд В | Результат |
| α (число или СЧА) | β (число или СЧА) | Генерируется случайное число, равномерно распределенное на интервале α ± β. Результат равен полученному числу |
| FN$DIS | Отсутствует | Результат равен значению функции DIS |
| Отсутствует | FN$B | Данная комбинация недопустима |
| FN$DIS | β (число или СЧА) | Вначале вычисляется значение функции DIS. Берется целая часть этого значения (пусть это будет число α), после чего генерируется случайное число, равномерно распределенное на интервале α ± β. Результат равен полученному числу |
| α (число или СЧА) | FN$DIS | Вначале вычисляется значение функции DIS (пусть это будет число (3), после чего находится произведение α × β. Результат равен целой части этого произведения |
| FN$DIS1 | FN$DIS2 | Вычисляются значение функций DISl и DIS2 (пусть это будет числа α и β), после чего находится произведение α × β. Результат равен целой части этого произведения |
Пример 21
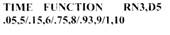
К этой функции можно обратиться таким образом:
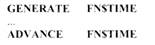
Пример 22
Пусть в моделируемой системе время обслуживания некоторым устройством распределено равномерно на интервале A ± 2, где среднее время обслуживания A c вероятностью 0,4 принимает значение 5, a c вероятностью 0,6 – значение 7. Эту ситуацию можно смоделировать следующим образом.
Определим функцию AVERAGET:

Используемее в блоке ADVANCE:
ADVANCE FN$AVERAGE_T,2
Выполнение подпрограммы блока ADVANCE включает расчет функции AVERAGE_T. Это, в свою очередь, требует обращения к генератору случайных чисел RN1. Пусть генератор выдал значение меньшее, чем 0,4. Тогда соответствующее значение функции AVERAGE_T равно 5. Таким образом, время задержки текущего транзакта в устройстве будет равномерно распределено на интервале 5±2.
Непрерывные случайные переменные, рассматриваемые как дискретные. Как известно, дискретные случайные переменные могут принимать только фиксированное число значений. В противоположность этому, непрерывные (в классическом смысле этого термина) случайные переменные могут иметь неограниченное число различных значений.
На практике обычно достаточно, чтобы все случайные переменные имели конечное число конкретных значений. Нет необходимости в тщательном определении значений этих случайных переменных, за исключением случаев, когда необходимо делать расчеты c высокой степенью точности. Таким образом, вполне возможна дискретизация непрерывных распределений. После этого они могут быть определены в GPSS c помощью дискретных и непрерывных GPSS-функций (непрерывные GPSS-функции по сути также являются дискретными, поскольку множество их значений дискретно и конечно).
Функции распределения случайных величин. В языке GPSS возможность задания функций распределения случайных величин ограничена заданием их в табличном виде путем аппроксимации непрерывными функциями. Поэтому можно задать только те функции, которые легко преобразовать для новых значений параметров. К таким функциям, например, относится функция экспоненциального распределения c параметром λ = 1, А также функция стандартного нормального распределения c математическим ожиданием т = 0 и стандартным отклонением σ = 1.
Эти ограничения не касаются языка GPSS World, в котором для задания различных вероятностных функций распределения можно использовать библиотечные процедуры, написанные на языке PLUS. Однако использование вероятностных распределений в табличном виде значительно ускоряет процесс моделирования.
Моделирование пуассоновского потока. Рассмотрим табличный способ задания пуассоновского потока заявок. Пуассоновский входящий поток описывается таким образом: вероятность поступления k заявок пуассоновского потока в течение интервала t составляет
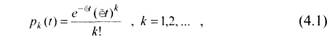
где λ – интенсивность потока.
Интервалы времени между соседними заявками пуассоновского потока распределены по экспоненциальному закону. Согласно методу обратной функции, можно получить ряд чисел, которые имеют экспоненциальное распределение, если ряд случайных чисел R, равномерно распределенных на интервале [0,1], преобразовать в соответствии c функцией, обратной к экспоненциальной функции распределения:
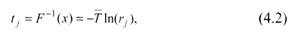
где tj – j -й разыгранный интервал времени поступления; 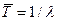 – средний интервал времени поступления; rj – j-e число в последовательности случайных чисел R c равномерным распределением на интервале [0, 1].
– средний интервал времени поступления; rj – j-e число в последовательности случайных чисел R c равномерным распределением на интервале [0, 1].
Разработчиками GPSS была осуществлена аппроксимация функции F-1 (x), обратной к экспоненциальной функции распределения c параметром λ = 1. Таким образом, функция F-1 (x) была заменена 23 отрезками, которые использовались для преобразования значений RNj в значение – ln(RNj).
Функция XPDIS определяет экспоненциальное распределение c интенсивностью λ = 1:

Пуассоновский входящий поток c интенсивностью λ, отличной от единицы, моделируется c помощью блока GENERATE таким образом:
1) в качестве операнда А используют среднее значение интервалов времени T= 1/ λ, где λ – интенсивность пуассоновского потока;
2) в качестве операнда В используют СЧА – значение функции XPDIS, операторы определения и описания которой приведены выше.
Пример 23
Пусть среднее значение интервалов поступления Т в пуассоновском потоке требований равно 2 ч, А единица времени в модели равна 1 мин, тогда поступление заявок моделируется блоком:
GENERATE 120,FN$XPDIS
Если необходимо моделировать задержку, распределенную no экспоненциальному закону со средним значением времени 345, то для этого используется блок:
ADVANCE 345,FN$XPDIS
Свойство ординарности пуассоновского потока гласит: вероятность поступления двух или более заявок в течение малого временного интервала равна нулю.
Пусть пуассоновский поток моделируется блоком
GENERATE 5,FN$XPDIS
Если в результате обращения к функции XPDIS полученное значение меньше, чем 1/5, то целая часть произведения числа 5 и значения функции XPDIS равна нулю. Отсюда следует нарушение свойства ординарности. Во избежание этого рекомендуется, чтобы операнд А в блоке GENERATE был больше 50. Это легко достигается путем варьирования значения единицы модельного времени.
Моделирование гипер– и гипоэкспоненциального распределений. Экспоненциальную функцию распределения можно использовать также для моделирования гипер – и гипоэкспоненциального распределений.
Неэкспоненциальное распределение c коэффициентом вариации* C > 1 можно получить c помощью взвешенной суммы экспонент – гиперэкспоненциального распределения:
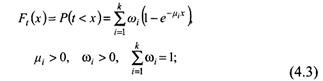
* Коэффициент вариации C – это отношение стандартного отклонения к математическому ожиданию случайной величины.
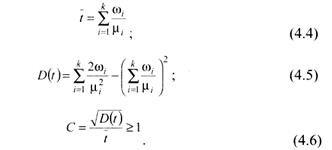
Если μ i = μ для всех i, то C = 1 – имеем экспоненциальное распределение.
Гиперэкспоненциальное распределение можно получить при параллельном соединении k (рис. 6) экспоненциальных обслуживающих устройств c интенсивностью обслуживания μi и вероятностью ωi использования для обслуживания 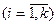 . Причем в произвольный момент времени может быть занято не более одного устройства из k. Такое распределение хорошо описывает распределение времени работы центрального процессора компьютера.
. Причем в произвольный момент времени может быть занято не более одного устройства из k. Такое распределение хорошо описывает распределение времени работы центрального процессора компьютера.

Рис. 6
Для моделирования гиперэкспоненциального распределения со средним значением 6,28 и стандартным отклонением 8,4 необходимо определить переменную
HYP FVARIABLE (410+(RN2'L'234)(#(1334-410)))#FN$XPDIS
Эту переменную можно использовать в блоке задержки так:
ADVANCE V$HYP
Гипоэкспоненциальное распределение c коэффициентом вариации C<1 описывается таким образом:
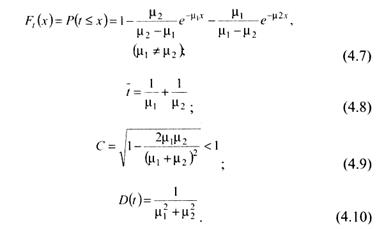
При равенстве всех коэффициентов μ распределение времени пребывания в обслуживающем центре (на рис. 7 обведен пунктирной линией) будет k-распределением Эрланга:
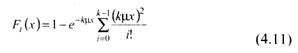
Гипоэкспоненциальное распределение характерно, например, для времени обслуживания устройств ввода-вывода. Его можно получить последовательным соединением обслуживающих экспоненциальных устройств, причем в любой момент времени должно быть занято не более одного устройства (рис. 7).

Рис. 7
Моделирование эрланговского потока. Экспоненциальное распределение не всегда адекватно описывает время обслуживания и поступления требований в систему. Более реалистичным является распределение Эрланга. В то же время, это распределение является частным случаем гамма-распределения, которое описано ниже. Для потока Эрланга k-го порядка c интенсивностью λ математическое ожидание и дисперсия определяются так: 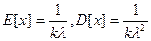 . Для моделирования распределения Эрланга может также использоваться экспоненциальная функция распределения. Как было показано в главе 1, для этого достаточно просуммировать k случайных экспоненциально распределенных величин. C ростом k распределение Эрланга будет приближаться к нормальному распределению. Например, поток Эрланга второго порядка со средним значением времени поступления 180 можно задать таким образом:
. Для моделирования распределения Эрланга может также использоваться экспоненциальная функция распределения. Как было показано в главе 1, для этого достаточно просуммировать k случайных экспоненциально распределенных величин. C ростом k распределение Эрланга будет приближаться к нормальному распределению. Например, поток Эрланга второго порядка со средним значением времени поступления 180 можно задать таким образом:

В нулевой момент времени в модель вводится транзакт. Этот транзакт в каждом их двух последующих блоков ADVANCE задерживается на экспоненциально распределенный промежуток времени. Блок SPLIT (подробнее см. в параграфе 19) создает копию транзакта и направляет ее на блок c меткой SDFG, исходный транзакт поступает в модель и т.д.
Пример 24
Для того, чтобы исследовать свойства распределения Эрланга можно воспользоваться следующей моделью:

Оператор TABLE, блоки SPLIT, SAVEVALUE и TABULATE использованы для сбора статистики об интервалах прихода транзактов в модель (об их назначении см. в параграфах 17, 19 и 21).
Построенная в результате моделирования гистограмма (при использовании оператора START 100000000) приведена на рис. 8. Читателю предлагается исследовать распределение Эрланга при различных значениях k, путем изменения количества блоков ADVANCE в приведенной программе.

Рис. 8
Моделирование нормального закона распределения. Функция стандартного нормального закона распределения c параметрами m = 0, σ = 1 задается в GPSS 24 отрезками следующим образом:

Для того, чтобы получить функцию нормального распределения случайной величины Х c математическим ожиданием тх ≠ 0 и среднеквадратичным отклонением σх ≠ 1, необходимо произвести вычисления по формуле

где Z – случайная величина со стандартной нормальной функцией распределения. Например, если случайная величина Х имеет параметры mx = 60 и σx = 10, то в GPSS эта случайная величина моделируется так:
NOR1 FVARIABLE 60+10#FN$NOR
Если необходимо осуществить задержку по этому закону распределения, то используется блок
ADVANCE V$NOR1
При использовании функции нормального распределения для блоков GENERATE и ADVANCE необходимо обеспечить неотрицательность значений интервалов поступления и задержки. Это можно сделать, если mx ≥ 5σx.
Моделирование других законов распределения. Все другие виды функций распределения случайных величин в GPSS/PC необходимо задавать табличным способом для конкретных значений параметров этих функций. Для этого можно использовать специальные программы, которые позволяют числовым способом вычислять необходимое значение числа отрезков аппроксимации этих функций, как это сделано, например, в системе ИСИМ [5]. Пример меню такой программы представлен на рис. 9.
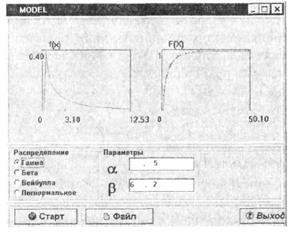
Рис. 9
Описание функции гамма-распределения для параметров (рис. 9):

Моделирование вероятностных функций распределения в GPSS World. В GPSS World в библиотеку процедур включено 24 вероятностных распределений. При вызове вероятностного распределения требуется определить аргумент Stream (может быть выражением), который определяет номер генератора случайных чисел. При моделировании генераторы случайных чисел создаются по мере необходимости и их явное определение не обязательно. Большинство вероятностных распределений имеют некоторые параметры. Аргументы процедур, называемые обычно Locate, Scale и Shape, часто используются для этих целей. Аргумент Locate используется после построения применяемого распределения и прибавляется к нему. Это позволяет горизонтально перемещать функцию распределения по оси X. Аргумент Scale обычно меняет масштаб функции распределения, А Shape – ее форму.
Встроенная библиотека процедур содержит следующие вероятностные распределения:
1) бета (Beta);
2) биномиальное (Binomial);
З) Вейбулла(Weibula);
4) дискретно-равномерное (Discrete Uniform);
5) гамма (Gamma);
6) геометрическое (Geometric);
7) Лапласа (Laplace);
8) логистическое (Logistic);
9) логлапласово (LogLaplace);
10) логлогистическое (LogLogistic);
11) логнормальное (LogNormal);
12) нормальное (Normal);
13) обратное Вейбулла (Inverse Weibull);
14) обратное Гаусса (Inverse Gaussian);
15) отрицательное биномиальное (Negative Binomial);
16) Парето (Pareto);
17) Пирсона типа V (Pearson Type V);
18) Пирсона типа VI (Pearson Type VI);
19) Пуассона (Poisson);
20) равномерное (Uniform);
21) треугольное (Triangular);
22) экспоненциальное (Exponential);
23) экстремального значения A (Extreme Value А);
24) экстремального значения В (Extreme Value В).
В качестве примера покажем, как для генерации потока транзактов можно использовать библиотечную процедуру экспоненциального распределения c параметром λ = 0,25 и использованием генератора случайных чисел RN1:
GENERATE (Exponential(l,0,(l/0.25)))
Из всех приведенных распределений опишем те, которые наиболее часто используются на практике.
Логарифмически нормальное распределение. Логарифмически нормальное распределение (логнормальное) – это распределение случайной величины, натуральный логарифм которой нормально распределен. Это распределение пригодно для моделирования мультипликативных процессов так же, как нормальное – для аддитивных.
C помощью центральной предельной теоремы можно показать, что произведение независимых положительных случайных величин стремится к логарифмически нормальной случайной величине.
Логнормальная случайная величина формируется под влиянием большого числа независимых факторов, причем каждый отдельный фактор оказывает равномерно незначительное и равновероятное по знаку влияние. Прирост каждого следующего фактора пропорционален уже достигнутому к этому времени значению исследуемой величины. To есть рассмотренный характер воздействия является мультипликативным.
Функция плотности логнормального распределения:
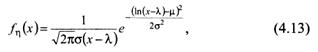
если Х > λ, в противном случае – f η (x) = 0.
Если после логарифмирования каждого элемента некоторого набора данных этот трансформированный набор данных нормально распределен, то исходные данные логарифмически нормально распределены.
Это распределение используется при моделировании экономических, информационных, физических и биологических систем. Оно хорошо моделирует процессы в случае, когда значение наблюдаемой переменной является случайной долей от значения предыдущего наблюдения.
Примерами использования этого распределения могут быть:
1) размеры и вес частиц, образуемых при дроблении;
2) доход семьи;
3) зарплата работников;
4) долговечность изделия, работающего в режиме износа и старения;
5) размер банковского вклада;
6) длины слов в языке;
7) длины передаваемых сообщений.
Например, когда неизвестно распределение длины передаваемых сообщений, размера файлов или длины запроса к базе данных, то c большой вероятностью можно предположить логнормальное распределение для этих величин.
Математическое ожидание и дисперсия логнормально распределенной случайной величины таковы:

где параметр σ задает среднеквадратическое отклонение, μ – математическое ожидание из нормального распределения, λ – величину сдвига для определения местоположения распределения.
Для вызова логнормального распределения используется библиотечная процедура
Не нашли, что искали? Воспользуйтесь поиском: