Основной закон динамики вращательного движения

Лабораторная работа № 15

ИЗУЧЕНИЕ ДВИЖЕНИЯ ГИРОСКОПА

Цель работы: изучение законов вращательного движения, изучение движения (прецессии) гироскопа под действием момента сил.

Теория работы

Основные понятия. Основной закон вращательного движения

Моментом импульса материальной точки L относительно точки О называется векторное произведение радиуса-вектора этой точки на вектор ее импульса p:

где r – радиус-вектор, проведенный из точки О в точку А, расположения материальной точки, p =m v – импульс материальной точки. Модуль вектора момента импульса:

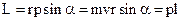
где a - угол между векторами r и p, l – плечо вектора p относительно точки О. Вектор L, согласно определению векторного произведения перпендикулярен к плоскости в которой лежат векторы r и p (или v), его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p по кратчайшему расстоянию, как показано на рисунке.

Моментом импульса относительно оси называется скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки на этой оси.

Моментом силы M материальной точки относительно точки О называется векторная величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку приложения силы, на силу F:

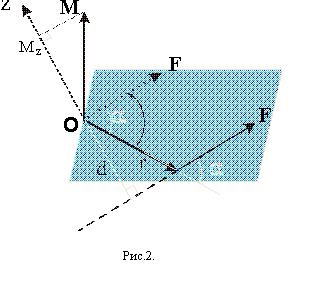. Модуль вектора момента силы:

где a - угол между векторами r и F, d = r*sina – плечо силы – кратчайшее расстояние между линией действия силы и точкой О. Вектор M (также как L) - псевдовектор, он перпендикулярен к плоскости в которой лежат векторы r и F, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F по кратчайшему расстоянию, как показано на рисунке. Значение и направление вектора M также можно рассчитать математически используя определение векторного произведения.

Моментом силы относительно оси называется скалярная величина, равная проекции на эту ось вектора момента силы M определенного относительно произвольной точки на этой оси.

Основной закон динамики вращательного движения

Для выяснения назначения приведенных выше понятий рассмотрим систему из двух материальных точек (частиц) и затем обобщим результат на систему из произвольного числа частиц (т.е. на твердое тело.)

Пусть на частицы с массами m₁, m₂ действуют внутренние f₁₂, f₂₁ и внешние силы F₁ и F₂.

Запишем второй закон Ньютона для каждой из частиц, а также вытекающую из третьего закона Ньютона связь между внутренними силами:

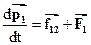(1)

(2)

(3)

Умножим векторно уравнение (1) на r₁, а уравнение (2) – на r₂ и сложим полученные выражения:

(4)

Преобразуем левые части уравнения (4), учитывая что

И векторы и параллельны и их векторное произведение равно нулю, тогда

(5)

Первые два слагаемых справа в (4) равны нулю, так как внутренние силы f₁₂, f₂₁ динаковы по величине и противоположно направлены (вектор r₁ - r₂ направлен по одной и той же прямой, что и вектор f₁₂).

(6)

Учитывая (5)и (6) из (4) получим

или

(7)

где L=L₁+L₂; M=M₁+M₂. Обобщая результат на систему из n частиц мы можем записать L=L₁+L₂+…+L_n= M=M₁+M₂ +M_n =

Уравнение (7) является математической записью основного закона динамики вращательного движения относительно точки: скорость изменения момента импульса системы равна сумме действующих на нее моментов внешних сил. Этот закон справедлив относительно любой неподвижной или движущейся с постоянной скоростью точки в инерциальной системе отсчета. Отсюда же следует закон сохранения момента импульса: если момент внешних сил М равен нулю, то момент импульса системы сохраняется (L=const).

Не нашли, что искали? Воспользуйтесь поиском: