Послойная кластеризация

Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами 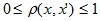, то .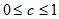

Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:
,
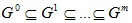где G^t = (V, E^t) — граф на уровне с^t,

,
с^t – t-ый порог расстояния,

m – количество уровней иерархии,

G⁰ = (V, o), o – пустое множество ребер графа, получаемое при t⁰ =1,

G^m = G, то есть граф объектов без ограничений на расстояние (длину ребер графа), поскольку t^m =1.

Посредством изменения порогов расстояния {с⁰, …, с^m}, где 0 = с⁰ < с¹ < …< с^m = 1, возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.

Нейронная сеть Кохонена

Нейронные сети Кохонена или самоорганизующиеся карты Кохонена (Kohonen’s Self-Organizing Maps) предназначены для решения задач кластеризации, когда обучающая последовательность образов отсутствует. Соответственно отсутствует и фиксация ошибки, на минимизации которой основаны алгоритмы обучения, например, алгоритм обратного распространения ошибки (Backpropagation).

Сеть Кохонена – это двухслойная нейронная сеть, содержащая входной слой (слой входных нейронов) и слой Кохонена (слой активных нейронов).

Слой Кохонена может быть: одномерным, двумерным или трехмерным.

В первом случае активные нейроны расположены в цепочку. Во втором случае они образуют двухмерную сетку (обычно в форме квадрата или прямоугольника), а в третьем случае они образуют трехмерную конструкцию.

В силу отсутствия обучающей последовательности образов, для каждого из которых известна от учителя принадлежность к тому или иному кластеру, определение весов нейронов слоя Кохонена основано на использовании алгоритмов классической классификации (кластеризации или самообучения).

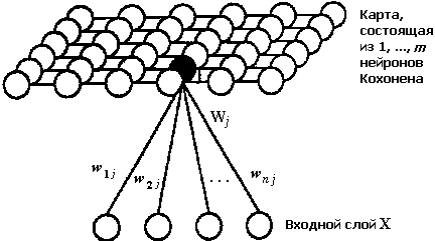
Рис.2. Пример топологической карты сети Кохонена

На рис. 2 приведен пример топологической карты сети Кохонена, содержащей входной слой и слой Кохонена. Нейроны входного слоя служат для ввода значений признаков распознаваемых образов. Активные нейроны слоя Кохонена предназначены для формирования областей (кластеров) различных классов образов. Каждый нейрон слоя Кохонена также соединен с соседними нейронами.

Поясним основной принцип работы сети Кохонена. Введем следующие обозначения (рис. 2):

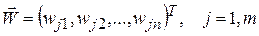(5.1)

– вектор весовых коэффициентов j -го нейрона слоя Кохонена,

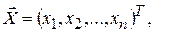(5.2)

– входной вектор или вектор значений признаков некоторого образца.

На стадии обучения (точнее самообучения) сети входной вектор X c попарно сравнивается со всеми векторами W j всех нейронов слоя Кохонена. Вводится некоторая функция близости (например, в виде эвклидова расстояния). Активный нейрон с номером слоя Кохонена, для которого значение функции близости d ( X, W c) между входным вектором X, характеризующим некоторый образ, и вектором W c максимально, объявляется «победителем». При этом образ, характеризующийся вектором X, относится к классу, который представляется «нейроном-победителем». В результате осуществляется преобразование n -мерного входного пространства R n на m -мерную сетку (слой Кохонена).

Следует подчеркнуть, что это отображение реализуется в результате рекуррентной (итеративной) процедуры самообучения (Unsupervised Learning). Отличительная особенность этого отображения – формирование кластеров. По завершении процесса самообучения на стадии реального использования сети Кохонена неизвестные входные образы относятся к одному из выявленных кластеров.

Сведения из теории вероятностей.

Случайная величина появляется как результат множественной реализации случайных событий 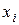, каждая из которых имеет вероятность появления 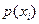. Очевидно, эти события могут группироваться вокруг определенных значений. При этом можно говорить о плотности распределения этих значений, плотности вероятностей .

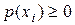Плотность распределения случайной величины несет исчерпывающую информацию о случайных величинах. Вместе с тем, на практике часто используют моменты этих распределений, характеризующих то или иное свойство.

Моменты 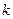-го порядка случайной величины 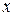выражаются значением

.

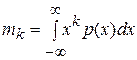Моментом 1-го порядка является математическое ожидание случайной величины

.

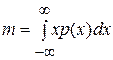Кроме моментов используют также и центральные моменты:

.

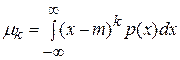Центральный момент 2-го порядка – это дисперсия

.

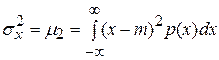Равномерное распределение. При равномерном распределении случайная величина 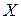может принимать значения, принадлежащие лишь отрезку 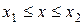, причем вероятности попадания в любые внутренние интервалы одинаковой ширины 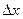равны. Тогда плотность вероятности

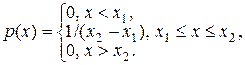
Гауссово (нормальное) распределение. Гауссова плотность вероятности

,

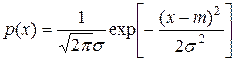содержащая два числовых параметра 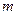- математическое ожидание и 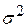- дисперсию.

Данный закон является широко распространенным, часто и обоснованно используется в теории систем. В соответствии с теоремой Шермана нормальный закон является наилучшей аппроксимацией неизвестного распределения. Важность закона подтверждается центральной предельной теоремой теории вероятностей, в соответствии с которой случайная величина 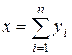, образованная как сумма 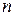-большого числа других случайных величин 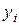, соизмеримых друг с другом, каждая из которых имеет произвольное распределение, имеет распределение, приближающееся к нормальному закону.

Математическая модель размещения радиоэлектронных средств (РЭС)

В качестве модели размещения РЭС СС в пространстве можно использовать модель Монте-Карло. Идея метода Монте-Карло состоит в следующем: производится “розыгрыш” – моделирование случайного явления с помощью некоторой процедуры, дающей случайный результат.

Конкретное осуществление процесса складывается каждый раз по-иному. Произведя такой “розыгрыш” большое число раз, получим статистический материал – множество реализаций случайного явления, который можно обрабатывать методами математической статистики.

Суть данной задачи состоит в том, чтобы в области ограниченной территории 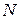выбрать случайно распределенные излучающие элементы с плотность распределения , где 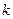- количество РЭС.

Моделирование случайного размещения РЭС целесообразно осуществлять путем генерирования координат РЭС 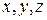с различными законами распределения. Наиболее возможными законами распределения являются:

1. Равномерное распределение с плотностью распределения

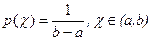, (5.3)

где и 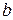- пределы изменения случайной величины;

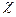- координаты .

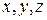2. Нормальное распределение с плотностью распределения

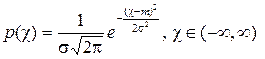, (5.4)

где и 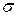математическое ожидание, и среднеквадратическое отклонение соответственно.

Не нашли, что искали? Воспользуйтесь поиском: