Критерий согласия Пирсона

Рассмотрим один из вопросов, связанных с проверкой правдоподобия гипотез, а именно – вопрос согласованности теоретического и статистического распределения.

Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой (рис. 5.3). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченный числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат так называемые «критерии согласия».

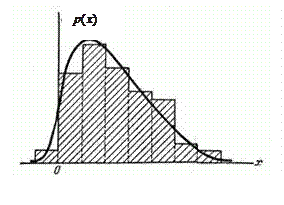Рис. 5.3

Идея применения критериев согласия заключается в следующем. На основании данного статистического материала нам предстоит проверить гипотезу 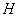, состоящую в том, что случайная величина 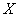подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения 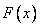или в виде плотности распределения или же в виде совокупности вероятностей 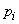, где 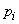- вероятность того, что величина 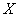попадет в пределы -го разряда.

Для того чтобы принять или опровергнуть гипотезу 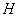, рассмотрим некоторую величину , характеризующую степень расхождения теоретического и статистического распределений. Величина может быть выбрана различными способами; например, в качестве можно взять сумму квадратов отклонений теоретических вероятностей 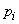от соответствующих частот 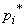или же сумму тех же квадратов с некоторыми коэффициентами («весами»), или же максимальное отклонение статистической функции распределения 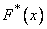от теоретической 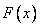и т. д. Допустим, что величина выбрана тем или иным способом. Очевидно, это есть некоторая случайная величина. Закон распределений этой случайной величины зависит от закона распределения случайной величины 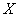, над которой производились опыты, и от числа опытов 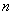. Если гипотеза верна, то закон распределения величины определяется законом распределения величины 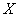и числом .

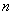Рассмотрим один из наиболее часто применяемых критериев согласия - так называемый «критерий » Пирсона.

Предположим, что произведено 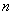независимых опытов, в каждом из которых случайная величина 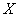приняла определенное значение. Результаты опытов сведены в 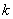разрядов и оформлены в виде статистического ряда:

			…………
			………….

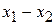
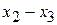
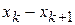
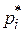
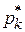
Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина 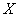имеет данный закон распределения (заданной функцией распределения 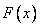или плотностью ). Назовем этот закон распределения «теоретическим».

Зная закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:

.

Проверяя согласованность теоретического и статистического распределений, мы будем исходить из расхождений между теоретическими вероятностями 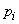и наблюденными частотами .

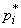Схема применения критерия к оценке согласованности теоретического и статистического распределений сводится к следующему:

1) Определяется мера расхождения по формуле:

, (5.5)

где 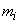- число значений в -м разряде.

2) Определяется число степеней свободы 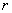как число разрядов 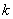минус число наложенных связей :

.

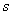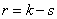Примерами таких связей может быть:

1.

,

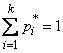если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);

2.

,

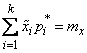если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое математическое ожидание и статистическое среднее значение;

3.

,

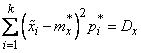если мы требуем, кроме того, совпадения теоретической и статистической дисперсий и т.д.

3) По 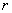и с помощью табл. 1 определяется вероятность того, что величина, имеющая распределение с степенями свободы, превзойдет данное значение .

4) Если эта вероятность меньше уровня значимости, гипотеза отбрасывается как неправдоподобная. Если эта вероятность больше или равна уровню значимости, гипотезу можно признать не противоречащей опытным данным.

Таблица 1.

Число степеней свободы	Вероятность P(χ2 > χα2)
0.95	0.9	0.8	0.7	0.5	0.3	0.2	0.1	0.05
	0.004	0.016	0.064	0.148	0.455	1.074	1.642	2.71	3.84
	0.103	0.211	0.446	0.713	1.386	2.41	3.22	4.6	5.99
	0.352	0.584	1.005	1.424	2.37	3.66	4.64	6.25	7.82
	0.711	1.064	1.649	2.2	3.36	4.88	5.99	7.78	9.49
	1.145	1.610	2.34		4.35	6.06	7.29	9.24	11.07
	1.635	2.2	3.07	3.83	5.35	7.23	8.56	10.64	12.59
	2.17	2.83	3.82	4.64	6.35	8.38	9.8	12.02	14.07
	2.73	3.49	4.59	5.53	7.34	9.52	11.03	13.36	15.51
	3.32	4.17	5.38	6.39	8.34	10.66	12.24	14.68	16.92
	3.94	4.86	6.18	7.27	9.34	11.78	13.44	15.99	18.31
	4.58	5.58	6.99	8.15	10.34	12.9	14.63	17.28	19.68
	5.23	6.3	7.81	9.03	11.34	14.01	15.81	18.55
	5.89	7.04	8.63	9.93	12.34	15.12	16.98	19.81	22.4
	6.57	7.79	9.47	10.82	13.34	16.22	18.15	21.1	23.7
	7.26	8.55	10.31	11.72	14.34	17.32	19.31	22.3
	7.96	9.31	11.15	12.62	15.34	18.42	20.5	23.5	26.3
	8.67	10.08	12.00	13.53	16.34	19.51	21.6	24.8	27.6
	9.39	10.86	12.86	14.44	17.34	20.6	22.8		28.9
	10.11	11.65	13.72	15.35	18.34	21.7	23.9	27.2	30.1
	10.85	12.44	14.58	16.27	19.34	22.8		28.4	31.4

Не нашли, что искали? Воспользуйтесь поиском: