Отличия реальных газов и паров от идеальных. Процессы парообразования. pv-диаграмма водяного пара 2 страница

Рассмотрим произвольный ТП 1-2 в координатах Q=f(t), где Q – подведенная теплота в Дж, t – температура в ⁰С. Тогда C_m= tgα, C= tgβ.

Если ТС – однородное рабочее тело, то в расчетах применяются относительные теплоемкости:

- удельная теплоемкость – теплоемкость, отнесенная к 1 кг вещества с=С/m, Дж/кгК.

- молярная теплоемкость – теплоемкость, отнесенная к 1 молю вещества 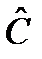=С/n, Дж/мольК.

- объемная теплоемкость – теплоемкость, отнесенная к 1 м³ вещества С’=С/n, Дж/ м³К.

Теплоемкость – функция процесса и зависит от рода рабочего тела, характера процесса и параметров состояния. Так, теплоемкость в процессе с постоянным давлением называется изобарной теплоемкостью:

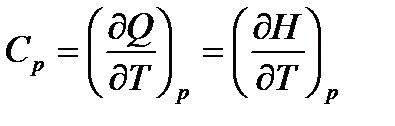, (23)

где Н, Дж – энтальпия.

Теплоемкость в процессе с постоянным объемом называется изохорной теплоемкостью:

, (24)

где U, Дж – внутренняя энергия.

Уравнение Майера связывает между собой теплоемкости идеального газа в процессах p=const и v=const.

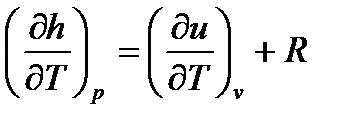, (25)

где R – удельная газовая постоянная, зависящая от рода газа, или 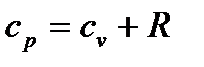, Дж/кгК.

Отношение изобарной теплоемкости к изохорной теплоемкости называется показателем адиабатного процесса:

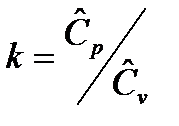. (26)

Для реальных газов показатель k зависит от температуры. Для воздуха и двухатомных газов показатель температуры k=1.4.

Для смеси газов теплоемкость вычисляется как сумма теплоемкостей газов, входящих в состав смеси:

. (27)

Сущность второго закона термодинамики. Различные формулировки закона. Вечный двигатель второго рода (АЗ: 2, СРС: 1)

Второй закон термодинамики устанавливает существование у всякой равновесной термодинамической системы однозначной функции состояния – энтропии S.

Понятие энтропии вводится в феноменологической термодинамике в помощью выражения dS=δQ/T, в соответствии с которым при подводе к ТС порции теплоты δQ энтропия системы возрастает. Температура Т в этом выражении есть температура на границе ТС в точке, где подводится порция теплоты δQ.

ТС находится в состоянии равновесия, если после ее изоляции от окружающей среды в ней не наблюдается никаких изменений, и в неравновесном состоянии, если после ее изоляции в ней обнаруживаются какие-либо изменения. Эти изменения в изолированной системе протекают самопроизвольно, и со временем система приходит в равновесное состояние. Процесс является неравновесным, если при его совершении ТС хотя бы в одной точке процесса находится в неравновесном состоянии.

Все равновесные процессы - обратимые, а неравновесные – необратимые процессы. Процесс называется необратимым, если суммарный запас энергии направленного, упорядоченного движения частиц ТС (работы) уменьшается, и обратимым, если этот запас энергии сохраняется. В необратимых процессах происходит диссипация энергии упорядоченного движения материи в энергию теплового, неупорядоченного движения, которую нельзя превратить ни в какой другой вид энергии в обратном направлении.

Второй закон термодинамики является обобщением опытных данных, указывает на особый характер протекания тепловых процессов и устанавливает пределы возможных превращений теплоты в работу. Этот закон позволяет определить направление и условия протекания любого термодинамического процесса. Дело в том, что тепловые процессы, удовлетворяющие первому закону термодинамики, подразделяются на самопроизвольные, протекающие без внешнего воздействия и на процессы, которые не могут происходить в данных условиях без внешнего воздействия.

В изолированной ТС самопроизвольные процессы протекают в направлении достижения равновесии системы. При этом работа преобразуется в теплоту, а теплота переходит лишь от тела с более высокой температурой к телу с более низкой температурой Процессы с превращением теплоты в работу в изолированной системе самопроизвольно идти не могут.

Наиболее краткой формулировкой 2-го закона термодинамики является формулировка Томсона-Кельвина: Теплота, содержащаяся в окружающей среде, не может быть превращена в работу теплового двигателя, если температура всех окружающих тел будет одинаковой, т.е. вечный двигатель 2-го рода неосуществим. Вечный двигатель второго рода – это двигатель, который производил бы механическую работу исключительно за счет теплоты окружающей среды с одинаковой температурой во всех ее точках.

Для обратимых процессов при подводе теплоты δQ извне изменение энтропии ТС равно изменению энтропии окружающей среды с обратным знаком, т.е.

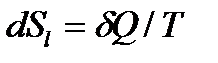, (28)

а в случае необратимых процессов

. (29)

При протекании процессов внутри ТС энтропия может только расти, т.е. .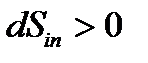

Различные формы записи объединенных уравнений. Характеристические функции и дифференциальные соотношения. Дифференциальные уравнения состояния, внутренней энергии, энтальпии и энтропии (АЗ: 4, СРС: 2)

Для сложных открытых ТС уравнения первого закона термодинамики, выраженные через изменения внутренней энергии и энтальпии имеют вид:

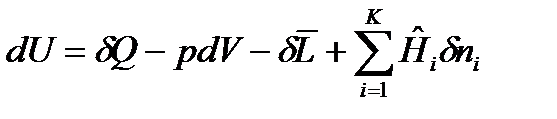, (30)

где 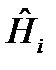- молярная энтальпия i-го вещества,

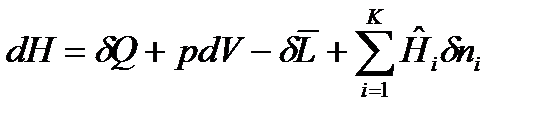. (31)

Математическое выражение 2-го закона термодинамики:

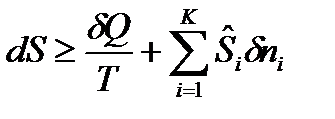, (32)

представим в виде и подставим в уравнение 1-го закона термодинамики.

Тогда получим объединенные выражения для изменения внутренней энергии и энтальпии 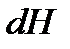: 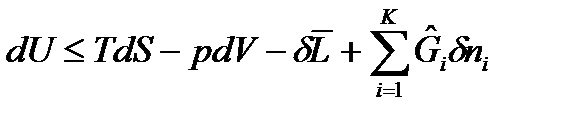, (33)

, (34)

где 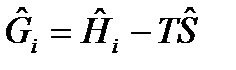- молярная свободная энергия Гиббса, Дж/моль.

Свободная энергия Гиббса, является функцией состояния. Функцией состояния является также свободная энергия Гельмгольца:

, Дж. (35)

Дифференциалы dF и dG – полные дифференциалы.

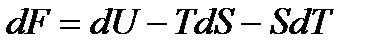, (36)

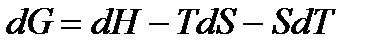. (37)

Характеристической функцией называется функция состояния ТС, позволяющая при соответствующем выборе независимых переменных (при определенных условиях сопряжения ТС с окружающей средой) выражать через свои производные наиболее просто и в явном виде термодинамические параметры, характеризующие свойства ТС. Построение термодинамического анализа на этих свойствах характеристических функций составляет основу метода характеристических функций.

Рассмотрим простую (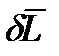 =0), закрытую ( 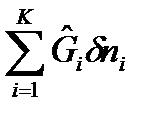=0) ТС. Тогда для обратимых процессов объединенные выражения 1-го и 2-го законов термодинамики будут иметь вид:

, (38)

, (39)

, (40)

. (41)

Каждое из этих уравнений (38)-(41) связывает пять переменных величин, которые зависят лишь от состояния ТС и не зависят от пути процесса. Функции U, H, F, G являются характеристическими только при определенном выборе независимых переменных: 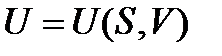, , 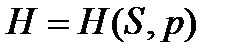, . Полные дифференциалы функций U, H, F, G имеют вид:

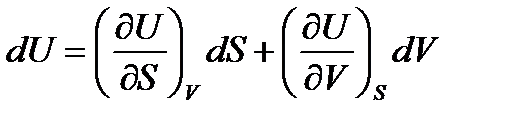, (42)

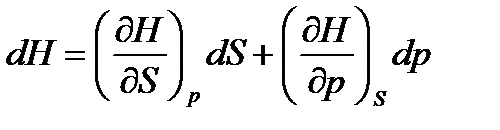, (43)

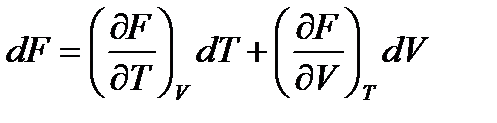, (44)

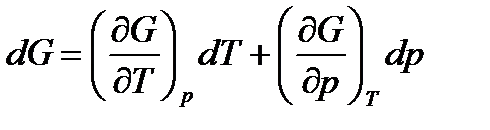. (45)

Сопоставляя уравнения (38) и (42) можно наиболее просто выразить неизвестные параметры – температуру Т и давление pс помощью частных производных внутренней энергии по энтропии Sи по объему V:

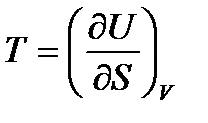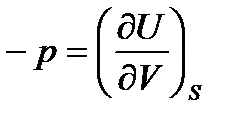, . (46)

По аналогии выразим другие неизвестные параметры:

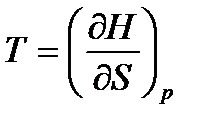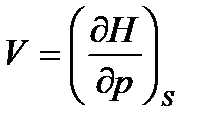, , (47)

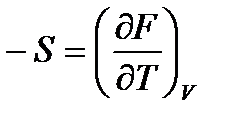, , (48)

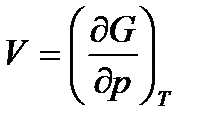, . (49)

Согласно свойству полного дифференциала вторая смешанная производная от функции U не зависит от порядка дифференцирования, т.е.:

, или (50)

.

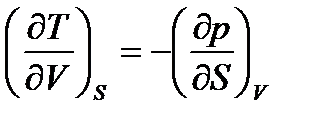По аналогии для функций H, F, G получим:

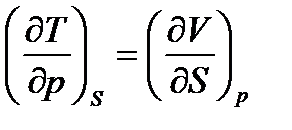, для H, (51)

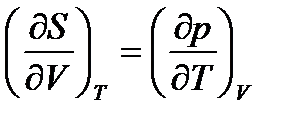, для F, (52)

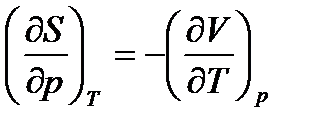, для G. (53)

Уравнения (50)-(53) называются дифференциальными соотношениями взаимности или уравнениями Максвелла.

Соотношение между изобарной и изохорной теплоемкостями в общем случае (АЗ: 2, СРС: 1)

Функция состояния ТС – энтропия может быть представлена в виде функциональной связи S=S(T, V). Дифференциал энтропии – полный дифференциал, т.е.

. (54)

Разделим уравнение (54) на dT и умножим на Т при условии p=const. Тогда имеем:

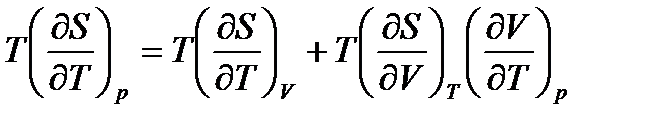. (55)

По определению 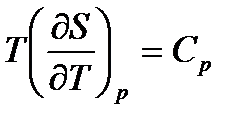и . После их подстановки в (55) получим:

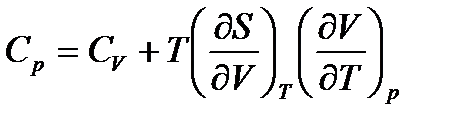. (56)

Производная 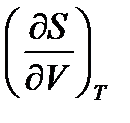включает энтропию и неудобна в расчетах. После ряда замен получим:

. (57)

Продифференцируем уравнение состояния идеального газа . Тогда

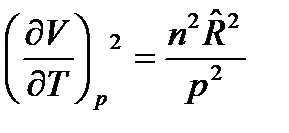и .

После подстановки этих выражений в (57) получим:

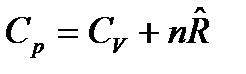. (58)

Условия равновесия однородных и неоднородных систем (АЗ: 2, СРС: 1)

Любая ТС может находиться либо в равновесном, либо в неравновесном состоянии. Условия термодинамического равновесия для различных сопряжений ТС с окружающей средой с фиксацией двух параметров определяются по поведению характеристических функций, которые позволяют судить о направлении протекания химических реакций и фазовых переходов.

Для простых (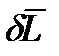 =0) и закрытых ( 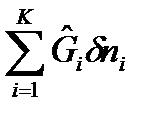=0) и закрытых ТС при фиксации двух параметров имеем:

,

,

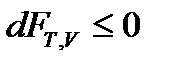, (59)

.

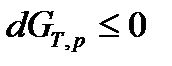Для необратимых процессов:

,

,

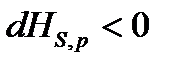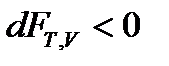, (60)

,

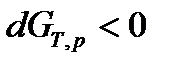т.е. необратимые, неравновесные процессы в простой, закрытой ТС протекают в направлении уменьшения соответствующего термодинамического потенциала. В состоянии равновесия значение соответствующего потенциала достигает минимума, и условия равновесия ТС имеют вид:

,

,

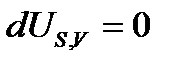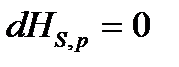, (61)

.

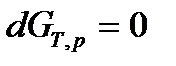Рассмотрим равновесие закрытых ТС, у которых, кроме условий сопряжения с окружающей средой, имеет место воздействие лишь одной силы немеханического характера. Тогда объединенные выражения 1-го и 2-го уравнений термодинамики примут вид:

,

,

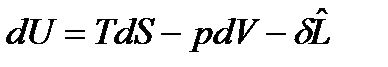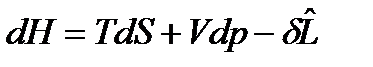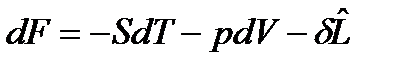, (62)

.

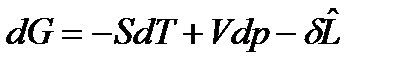Работу немеханического характера 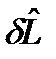в (62) будем представлять в виде:

, Дж, (63)

где А – термодинамическое сродство, Дж/моль, - путь термодинамического процесса, моль.

Термодинамическое сродство вводится соотношением:

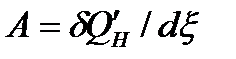, Дж/моль, (64)

где 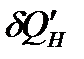– некомпенсируемая теплота, т.е. количество работы, которое диссипировало (рассеялось) в энергию теплового движения частиц на длине пути процесса. Т.о., термодинамическое сродство – это количество энергии упорядоченного движения частиц (работы), которое диссипировало (рассеялось) на длине пути процесса внутри ТС. При А=0 – процесс обратимый, при А>0 – процесс необратимый. После подстановки выражения (63) в уравнения (62) получим:

,

,

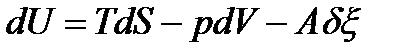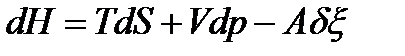, (65)

.

Таким образом, 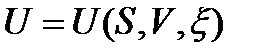, , 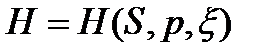, 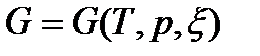и при фиксации двух первых параметров в уравнениях (65) будем иметь:

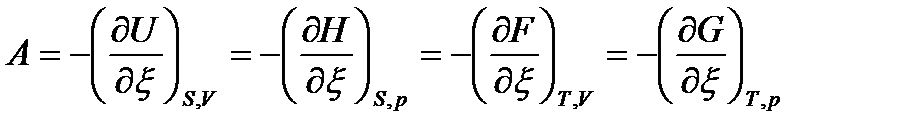. (66)

Следовательно, термодинамическое сродство определяется через частные производные характеристических функций по пути процесса.

Примером термодинамического сродства является химическое сродство, В этом случае величина пути процесса называется пробегом химической реакции.

Равновесное состояние ТС можно охарактеризовать также по изменению энтропии. При необратимых, неравновесных процессах внутри адиабатной, закрытой ТС изменение энтропии 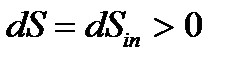, т.е. энтропия растет и достигает максимума в состоянии равновесия: , .

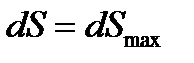Фазовые переходы I рода. Уравнение Клапейрона-Клаузиуса. Фазовые переходы II рода (АЗ: 2, СРС: 1)

Переход вещества от одной фазы в другую – фазовый переход – всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).

Различают фазовые переходы двух родов. Фазовый переход первого рода (например, плавление, кристаллизация и т.д.) сопровождается поглощением или выделением вполне определённого количества теплоты, называемой теплотой фазового перехода.

Пар – это газ над поверхностью жидкости, а испарение – это переход из жидкой фазы в газообразную (паровую). Кипение – это превращение жидкости в пар по всему ее объему.

Конденсация – это переход из паровой фазы в жидкую. Сублимация – переход из твердой фазы в газообразную. Десублимация – переход из газовой фазы в твердую.

Равномерная смесь мельчайших частиц жидкости и сухого насыщенного пара образует влажный насыщенный пар. При переходе всей жидкости в пар образуется сухой насыщенный пар. Насыщенный пар – это пар, находящийся в равновесии с жидкостью. Ненасыщенный пар – это пар, не находящийся в равновесии с жидкостью

Перегретым паром называется пар, температура которого выше температуры сухого насыщенного пара при данном давлении.

Степенью сухости: , или 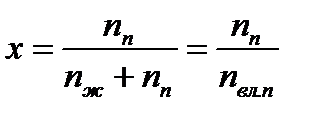, называется массовая или молярная доля сухого насыщенного пара в смеси пара (индекс «п») с жидкостью (индекс «ж»). Для горячей воды при температуре насыщения (кипения) – t_s степень сухости х=0. Для сухого насыщенного пара степень сухости х=1. Величина: у=1-х, называется степенью влажности пара.

Фазовая диаграмма р-Т для однокомпонентной равновесной термодинамической системы имеет вид, представленный на рисунке:

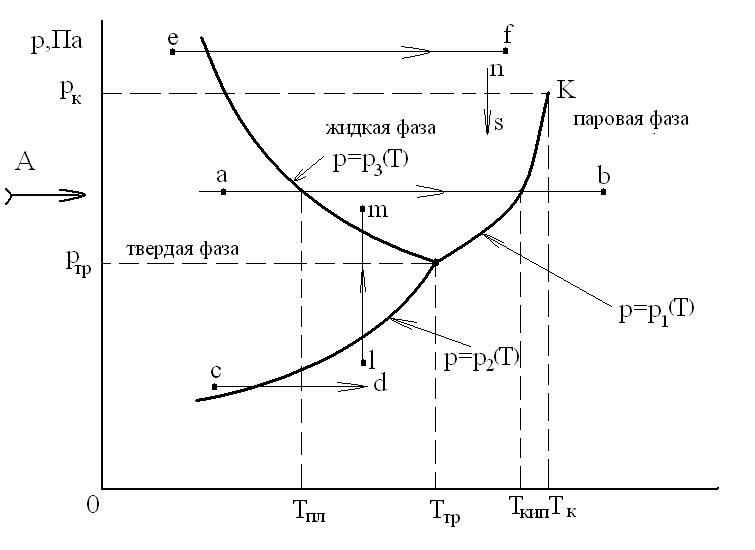
Равновесное существование 3-х фаз возможно только при определенных давлении ртр и температуре Ттр. Это состояние ТС называется тройной точкой, и что число степеней ее свободы равно нулю. Для воды значения: Ттр=273,15К и ртр=1 физич. атм.

Для двухфазной ТС существует однозначная зависимость р=р(Т), т.е. ТС обладает одной степенью свободы.

В однофазной ТС независимо могут изменяться два термодинамических параметра: давление р и температура Т (ТС обладает двумя степенями свободы).

На фазовой р-Т диаграмме линия р=р1(Т) является кривой парообразования (испарения), на которой сосуществуют, т.е. находятся в равновесии, жидкая и паровая фазы.

Линия– р=р2(Т) - это кривая сублимации, на которой находятся в равновесии твердая и паровая фазы. При этом подводятся энергия, равная теплоте сублимации.

Линия р=р3(Т) - кривая плавления, на которой находятся в равновесии твердая и жидкая фазы.

Кривая парообразования р=р1(Т) оканчивается для каждого вещества в точке К при определенных критических значениях давления рк и температуры Тк.

Получим условие равновесия ТС, рассматривая бесконечно малый цикл Карно (обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов) при переходе «жидкость-пар» в p-v и T-s координатах:

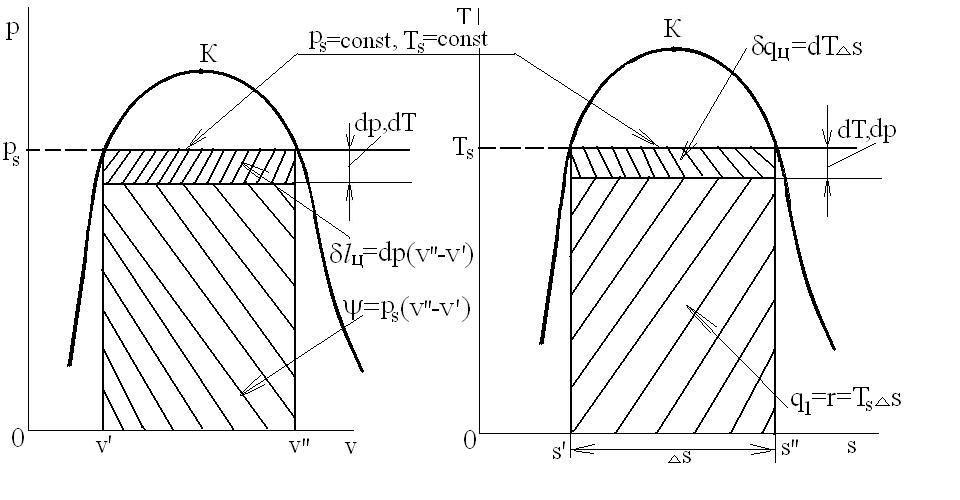
Термический КПД цикла Карно равен:

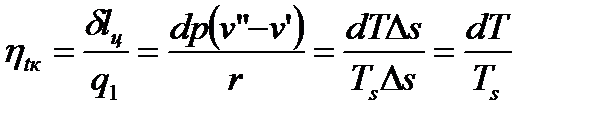. (67)

Отсюда имеем:

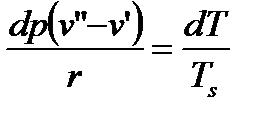, или (68)

. (69)

Это уравнение Клапейрона-Клаузиса.

При переходе «жидкость-пар» удельный объем растет, т.е. 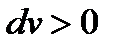и 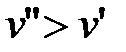, теплота парообразования 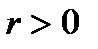и 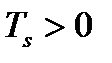. Поэтому величина 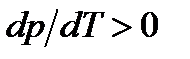, т.е. положительна. Таким образом, давление насыщенного пара над жидкостью для фаз, находящихся в равновесии, всегда возрастает с ростом температуры.

Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объёма, называются фазовыми переходами второго рода. Эти переходы характеризуются постоянством объёма и энтропии, но скачкообразным изменением теплоёмкости. Примерами фазовых переходов второго рода являются: переход ферромагнитных веществ (железа, никеля) при определённых давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия при Т=2,9К в другую жидкую модификацию, обладающую свойствами сверхтекучести.

Отличия реальных газов и паров от идеальных. Процессы парообразования. pv-диаграмма водяного пара

Идеальный газ — газ, в котором взаимодействие между молекулами сводится к парным столкновениям, причём время межмолекулярного столкновения много меньше среднего времени между столкновениями. Идеальный газ является простейшим модельным объектом молекулярной физики.

Уравнение состояния идеального газа

Реальный газ — газ, в котором учитывается взаимодействие между молекулами. Уравнение состояния реального газа часто строится методами теории возмущений, при этом отличие от уравнения состояния идеального газа описывается набором вириальных коэффициентов.

Паровая диаграмма p-v. Расчет количества теплоты, затраченной на процесс парообразования

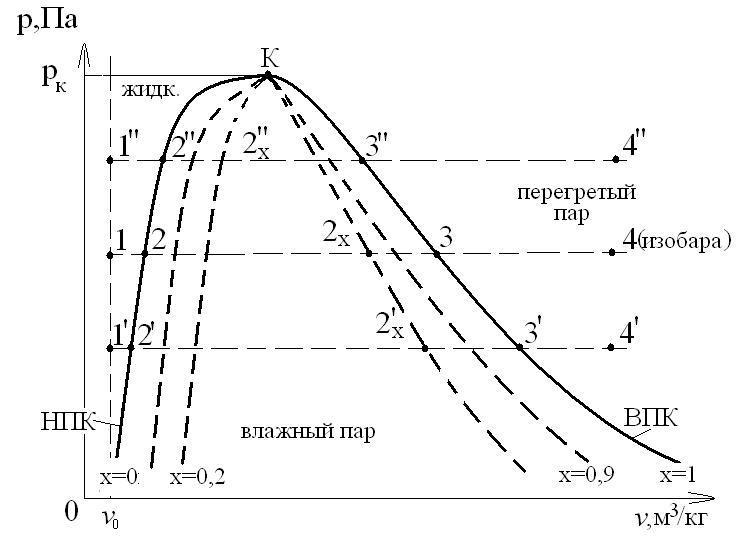
НПК – нижняя (левая) пограничная кривая (х=0) отражает состояние горячей воды при температуре насыщения t=t_s=t_кип.

ВПК – верхняя (правая) пограничная кривая (х=1) отражает состояние сухого насыщенного пара. Равновесие системы: «жидкость-пар», - динамическое равновесие. При рассмотрении процессов с паром используются следующие стандартные обозначения параметров, представленные в виде таблицы:

№ п/п	Состояние	Обозначения параметров	Точка на диаграмме
	Горячая вода при t=ts(х=0) НПК		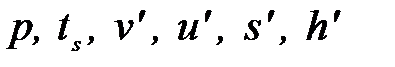т.2
	Сухой насыщенный пар (х=1), ВПК		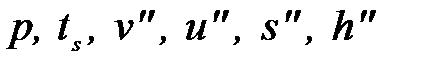т.3
	Влажный пар при степени сухости «х»		т.2х
	Перегретый пар		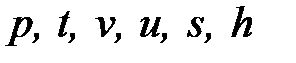т.4

Образование водяного пара проходит 3 стадии:

Подогрев жидкости от 0⁰С до температуры кипения (насыщения) ts (процесс 1-2).

Парообразование при t_s=const (t_s= ).

Перегрев пара от t_s до t_пер.

Рассмотрим процесс «1-2» - нагрев жидкости. В т.1 температура холодной воды t0=00С при давлении р. При подводе теплоты q по изобаре (p=const) вода нагревается от 00С до t_s:

В изобарно-изотермическом процессе парообразование «2-3» (p_s=const, T_s=const) подводится теплота парообразования.

В процессе «3-4» теплота q_пер идет на перегрев пара от температуры t_s до t_пер при p=const:

Пар высокого давления требует меньше теплоты для своего образования, т.е. является более экономичным при р>40.105Па.

1.7.2. Основные параметры воды и водяного пара. Таблицы водяного пара. Ts и hs диаграммы. Влажный воздух (АЗ: 2, СРС: 1)

Степенью сухости: , (70)

или 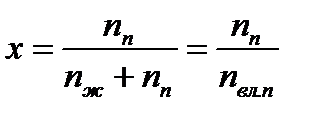, (71)

называется массовая или молярная доля сухого насыщенного пара в смеси пара (индекс «п») с жидкостью (индекс «ж»).

Паровая диаграмма «T-s»

При 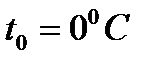удельная энтропия 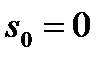. Тогда процессы нагрева жидкости (1-2), парообразования (2-3) и перегрева пара (3-4) будут иметь вид, как показано на следующем рисунке:

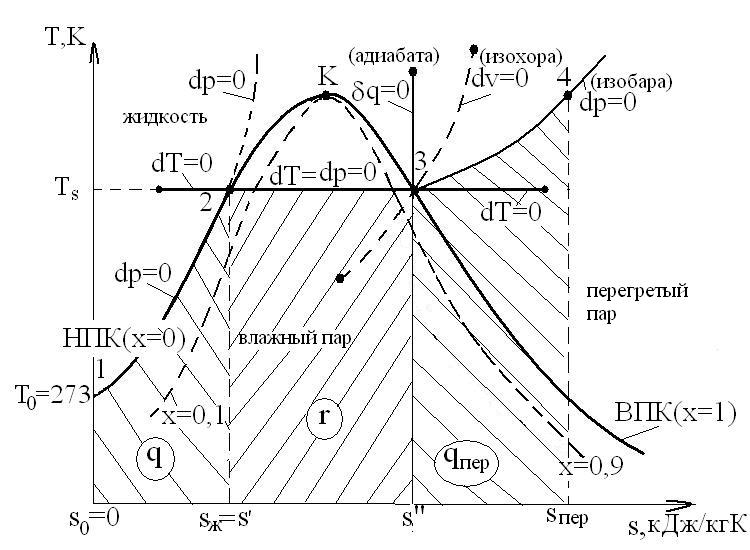
1. Процесс (1-2) нагрева жидкости при p=const. При этом изобара практически совпадает с НПК, так как термическая расширяемость жидкости мала.

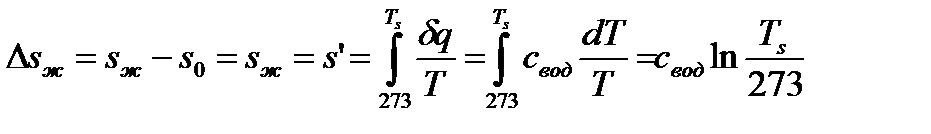. (72)

Таким образом:

. (1) (73)

2. Процесс (2-3) парообразования при .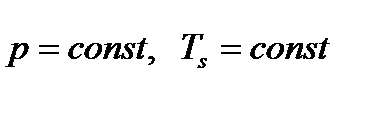

или . (74)

Площадь под изотермой 2-3 равна теплоте парообразования r.

3. Процесс (3-4) – перегрев пара

. (75)

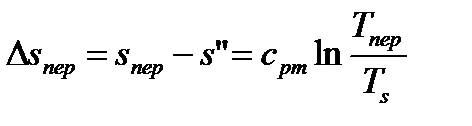. ((76)

Не нашли, что искали? Воспользуйтесь поиском: