Отличия реальных газов и паров от идеальных. Процессы парообразования. pv-диаграмма водяного пара 3 страница

Энтропия влажного пара:

. (77)

Энтропия сухого насыщенного пара (х=1).

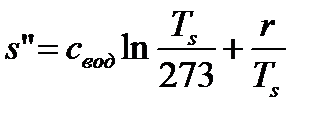. (78)

Энтропия перегретого пара:

. (79)

Изобара в области перегретого пара (3-4) идет более круто, чем изобара в области нагрева воды (1-2).

На паровой диаграмме «h-s» критическая точка «К» сдвинута влево и вниз по отношению к вершине, так как энтальпия «hк» в критической точке не является максимальной величиной. Так для воды 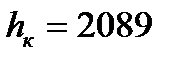кДж/кг, а кДж/кг при давлении р=30-40 ата.

Как уже отмечалось, при построении диаграммы «h-s» принимается, что при температуре t0=00C величины энтальпии, внутренней энергии и энтропии равны нулю, т.е. 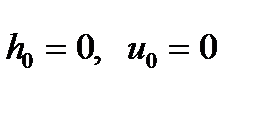и 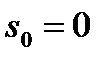(см. диаграмму «h-s»).

Процесс 1-2 – подогрев жидкости при : теплота жидкости 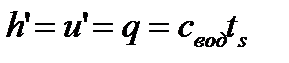, энтропия 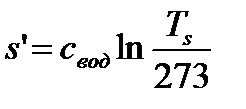. (80)

Процесс 2-3 – парообразование (прямая наклонная линия в области влажного пара):

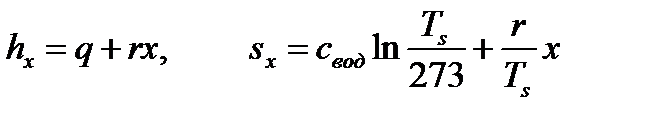. (81)

Для сухого насыщенного пара (т.3):

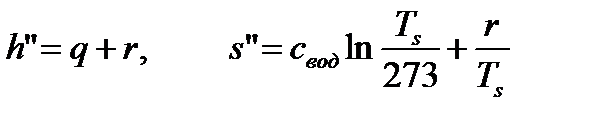. (82)

Для перегретого пара (т.4):

, (83)

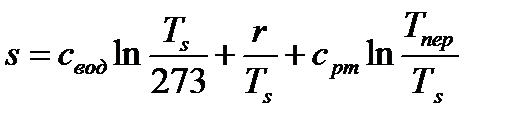. (84)

Положение точек на диаграмме «h-s» определяется заданием следующих параметров:

для влажного пара заданием давления (р) и степени сухости (х);

для сухого насыщенного пара (х=1) заданием давления (р);

для перегретого пара заданием давления (р) и температуры (Т).

По положению точки на диаграмме «h-s» можно определить все параметры этого состояния, рассчитать теплоту и внешнюю работу любого процесса. В диаграмме «h-s» теплоты выражаются прямыми линиями. Поэтому расчет паровых процессов в энергетической части более удобно проводить по диаграмме «h-s», чем по диаграмме «Т-s», где теплоты выражаются площадями под кривой процесса, которые надо измерять планиметром.

Расчет теплоты, работы и изменений внутренней энергии с помощью паровой диаграммы «h-s» проводится в следующем порядке:

- по условию задания наносят на диаграмму график процесса 1-2;

- по положению крайних точек процесса «1-2» определяют все параметры пара а начале: 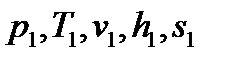, и в конце: 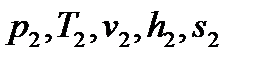, процесса;

- по общей для всех процессов формуле определяется изменение внутренней энергии пара в процессе «1-2»:

.

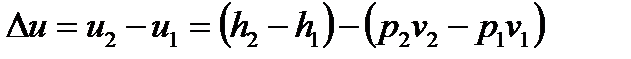Для пара в изотермическом процессе величина 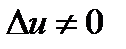и 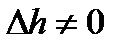(как известно, для идеального газа в процессе T=const 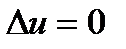и 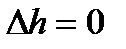). Это связано с тем, что в процессе парообразования внутренняя теплота испарения 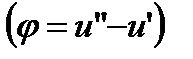идет на преодоление внутреннего сцепления между молекулами (работу дисгрегации), которая зависит как от температуры, так и от давления;

- определяется теплота, сообщенная пару в процессе «1-2»:

при ;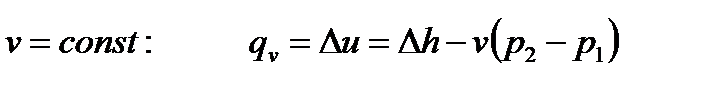

при ;

при ;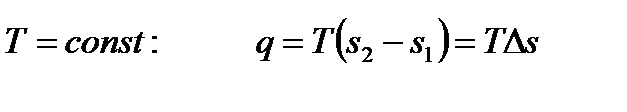

при адиабатном процессе: и ;

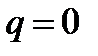- определяется внешняя работа пара по общему выражению 1-го закона термодинамики: .

1.8.1. Основные уравнения процессов течения. Течение газа в каналах переменного сечения (АЗ: 2, СРС: 0,5)

Непрерывное течение газа рассматривается в термодинамике как равновесный процесс. Принимается, что течение – пространственно одномерное, т.е. параметры потока газа: давление р, температура Т, скорость w и плотность 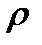и др. изменяются только в направлении течения и, что течение - стационарное (установившиеся), т.е. параметры не изменяются во времени 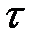; расход газа G=const();

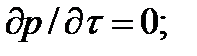
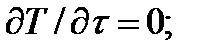
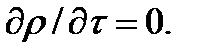
Принимается также, что течение - адиабатное, т.е. 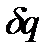=0, изоэнтропийное, т.е. ds=0, что техническая работа не совершается и что пьезометрическая высота не изменяется (dy=0).

Для определения параметров потока (W, p, T, ) в каждом поперечном сечении по длине канала fx решается при сделанных допущениях следующая система уравнений:

- уравнение энергии (уравнение 1-го закона термодинамики):

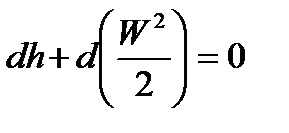; (85)

- уравнение движения (Бернулли):

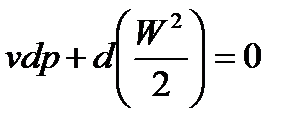; (86)

- уравнение неразрывности (уравнение расхода):

; (87)

- уравнение состояния для газа:

,

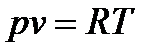и для несжимаемой жидкости: 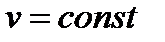. (88)

Уравнения энергии (85), Бернулли (86) и неразрывности (87) справедливы для жидкостей и газов. Запись уравнения состояния (88) определяет в каком состоянии: жидком или газообразном, находится ТС. Из сопоставления уравнений (85) и (86) следует, что

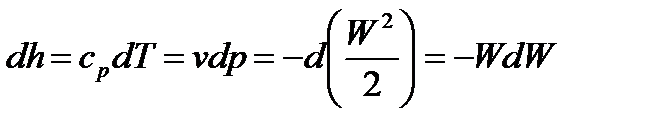, (89)

т.е. с ростом скорости W в адиабатном потоке газа его энтальпия h, температура Т и давление р уменьшаются.

Уравнение обращения воздействий отражает воздействие на параметры потока формы канала. Для его вывода рассмотрим стационарное течение в канале (G=const). Из уравнения расхода:

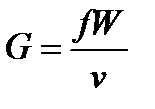, или 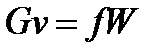, (90)

после его дифференцирования имеем:

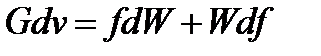. (91)

Разделим выражение (91) на уравнение (90) почленно.

Тогда имеем:

, или 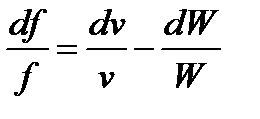. (92)

Из уравнения адиабатного процесса

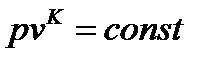, (93)

после дифференцирования получим:

,

или 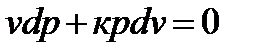. (94)

Разделим выражение (95) на 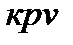. Тогда:

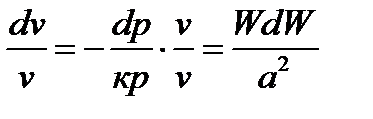. (95)

где ; а – скорость звука, м/с; - vdp=WdW – уравнение Бернулли. После подстановки выражения (95) в уравнение (92) имеем:

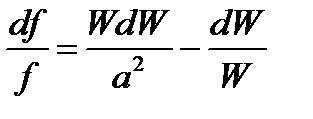, (96)

или

, (97)

где 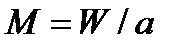- число Маха. Правая часть уравнения обращения воздействий для адиабатного изоэнтропийного течения идеального газа (97) содержит основные параметры потока: число Маха и изменение скорости 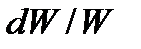, а левая часть – отражает воздействие на течение среды изменения площади поперечного сечения канала df, т.е. формы канала.

Рассмотрим воздействие формы канала df на адиабатное течение в соплах и диффузорах. Сопла – это каналы, в которых происходит расширение газа и увеличение скорости его движения. В диффузорах происходит сжатие газа и уменьшение скорости его движения.

Для течения в соплах, где газ расширяется и скорость растет dW>0. При этом знак df будет одинаковым со знаком скобки (М²-1) уравнения (97).

Если на входе в сопло число Маха M<1 и разность (М²-1) – отрицательна, то сопло является суживающимся, т.е. df<0.

Если на входе в сопло число Маха М>1, то разность (М²-1) – положительна и df>0, т.е. сопло – расширяющееся. Увеличение скорости течения при М>1 происходит за счет увеличения площади поперечного сечения канала.

В диффузорах, где происходит сжатие газа и уменьшение скорости его движения, dW<0 и знак df противоположен знаку выражения (М²-1). При M>1 df<0, т.е. диффузор суживающийся. При M<1 df>0, т.е. диффузор расширяющийся.

Таким образом, один и тот же канал в зависимости от величины скорости газа на входе в канал может работать и как диффузор и как сопло. В суживающемся сопле нельзя достичь скорости газа, большей, чем местная скорость звука. Для получения скорости истечения большей скорости звука должны применяться комбинированные сопла – сопла Лаваля.

Скорость адиабатного потока. Истечение газа из сосуда неограниченной емкости (АЗ: 2, СРС: 0,5)

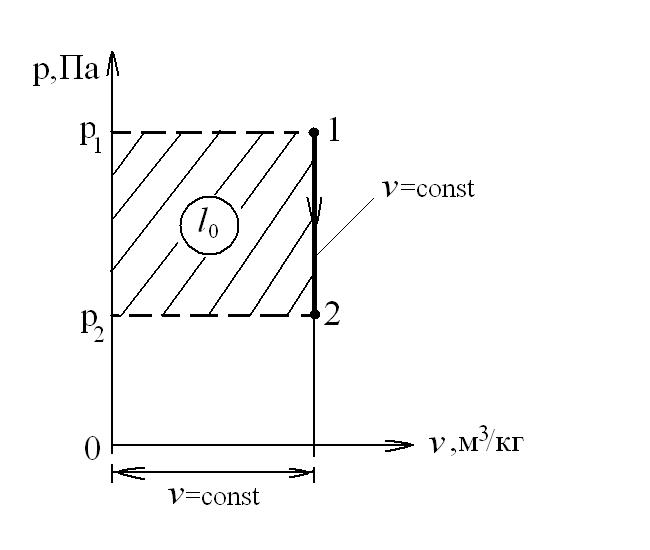
Рассмотрим истечение газа из сосуда неограниченной емкости. В этом случае параметры на входе в сопло равны параметрам торможения 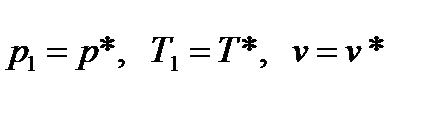, а скорость W₁=0. Скорость на выходе из сопла с площадью поперечного сечения f₂ равна скорости истечения W₂=W, а давление газа на выходе из сопла – давлению окружающей среды р₂. Схема сопла представлена на следующем рисунке:

Располагаемая работа при адиабатном течении газа в сопле идет на увеличение кинетической энергии потока газа:

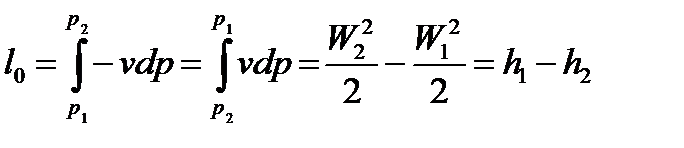. (98)

В p-v координатах располагаемая работа равна:

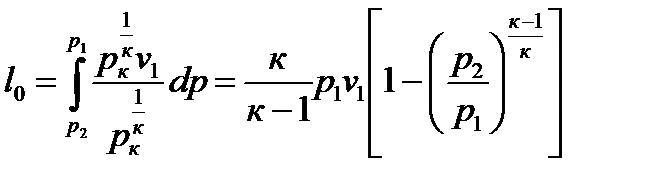. (99)

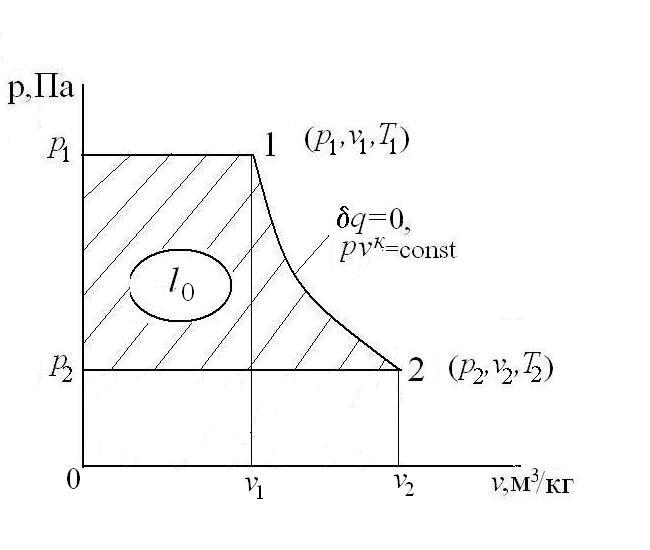
В h-s координатах: l₀=h₁-h₂

В T-s координатах: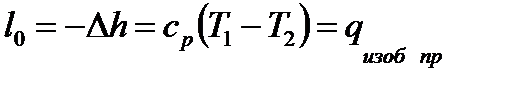

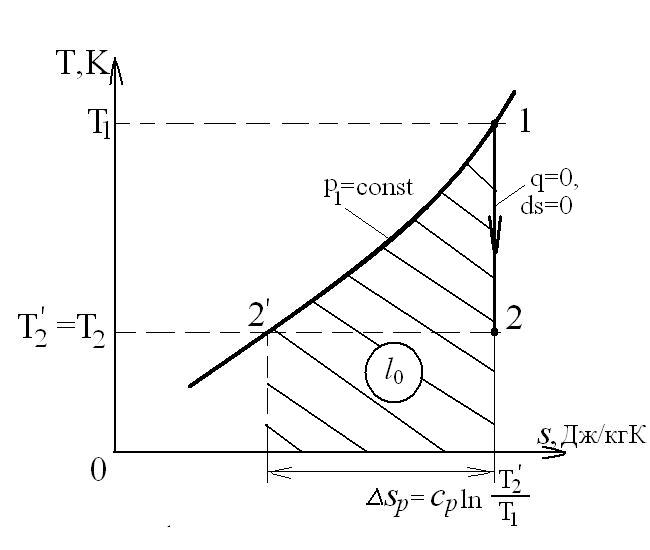
Располагаемая работа при течении в сопле несжимаемой жидкости (v=const) равна:

. (100)

Расчет скорости истечения газа

Скорость истечения газа определяется из выражения .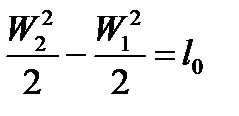

Тогда 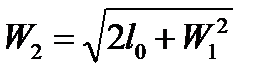, при 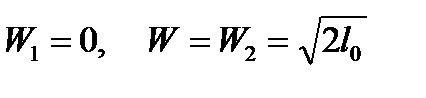. (101)

Тогда имеем: 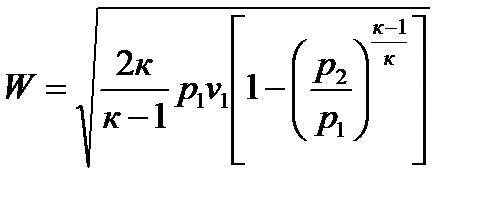, м/с, или

, м/с. (102)

Скорость истечения газа зависит от состояния газа на входе в сопло и глубины его расширения, т.е. от отношения давлений газа р₂/р₁.

Если выразить располагаемую работу через изменение энтальпий газа, то получим

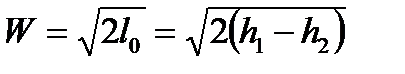, м/с. (103)

Таким образом, скорость истечения газа зависит от значений энтальпий газа перед соплом и на выходе из него.

Максимальная скорость истечения газа будет при его истечении в вакуум, т.е. при р₂=0:

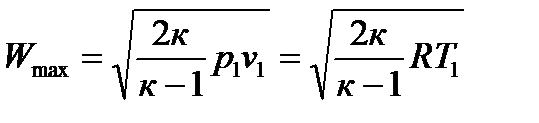. (104)

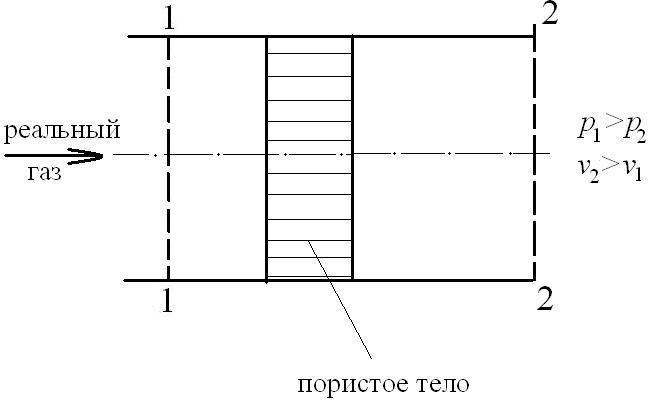
Дросселирование газов и паров. Кривые инверсии (АЗ: 2, СРС: 1)

Процесс течения газа или пара через местное гидравлическое сопротивление, например, диафрагму в трубопроводе при отсутствии теплообмена (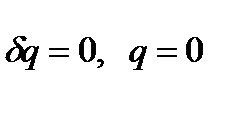) называется адиабатным дросселированием газа или пара. Этот процесс течения газа представлен на следующем рисунке:

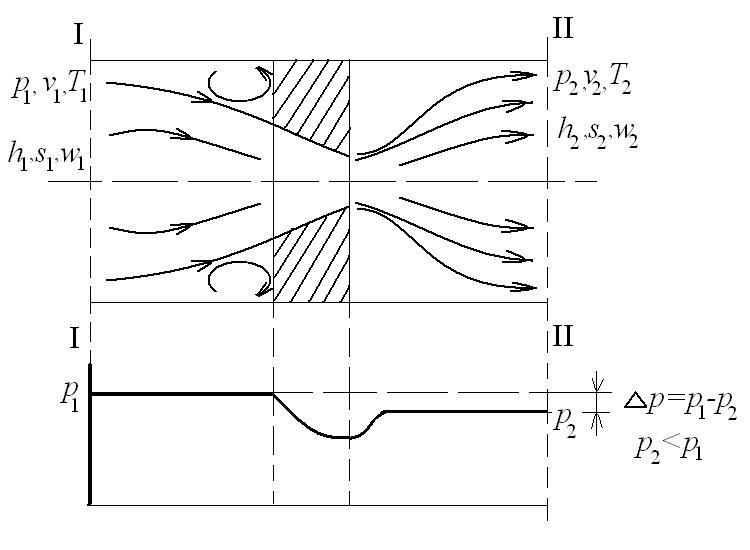
При дросселировании скорость газа в узком сечении диафрагмы увеличивается, а температура уменьшается. После прохождения диафрагмы скорость и температура в сечении II-II восстанавливаются. При этом скорость 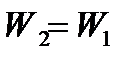, а температура Т₂ для идеального газа Т₂=Т₁ и для реальных газов и паров Т₂ Т₁. Тогда из уравнения 1-го закона термодинамики имеем изменение энтальпии при дросселировании:

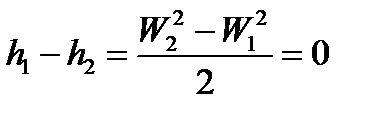, т.е. 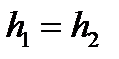. (105)

Таким образом, процесс дросселирования газа 1-2 является изоэнтальпийным (h=const), как показано на следующем рисунке:

В процессе 1-2 происходят необратимые явления (трение, вихреобразование) и энтропия растет: .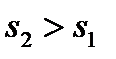

Из объединенного выражения 1-го и 2-го законов термодинамики: 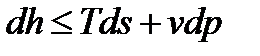, при dh=0 имеем: .

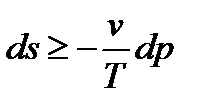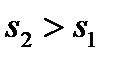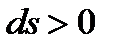Поскольку и , то 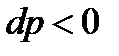, т.е. давление при дросселировании газа может только уменьшаться, а его удельный объем – увеличиваться, т.е. .

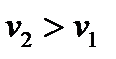Величина потерь давления в процессе дросселирования газа зависит от природы и состояния газа, а также от его скорости, относительного сужения канала и других параметров. Функция 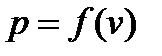убывающая и ее производная при величина отрицательная, т.е. .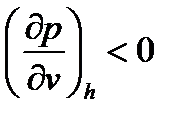

Таким образом, можно сделать вывод, что при дросселировании газа: , а температура газа либо увеличивается, либо уменьшается, либо остается неизменной (для идеального газа и для точек инверсии в случае реального газа Т₂=Т₁).

Эффект Джоуля-Томсона – это явление изменения температуры газа при адиабатном дросселировании, когда происходит расширение газа без совершения внешней работы и без теплообмена за счет преодоления гидравлического сопротивления 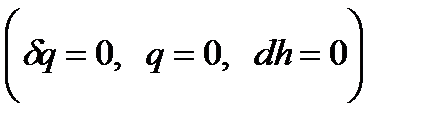. При этом затрачивается работа проталкивания :

Эффект Джоуля-Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (ΔТ < 0), и отрицательным, если газ нагревается (ΔТ > 0).

Согласно молекулярно-кинетической теории строения вещества, Эффект Джоуля-Томсона свидетельствует о наличии в газе сил межмолекулярного взаимодействия (обнаружение этих сил было целью опытов Джоуля и Томсона). Действительно, при взаимном притяжении молекул внутренняя энергия (U) газа включает как кинетическую энергию молекул, так и потенциальную энергию их взаимодействия. Расширение газа в условиях энергетической изоляции не меняет его внутренней энергии, но приводит к росту потенциальной энергии взаимодействия молекул (поскольку расстояния между ними увеличиваются) за счёт кинетической. В результате тепловое движение молекул замедлится, температура расширяющегося газа будет понижаться. В действительности процессы, приводящие к Эффекту Джоуля-Томсона, сложнее, т.к. газ не изолирован энергетически от внешней среды. Он совершает внешнюю работу (последующие порции газа, справа от дросселя, теснят предыдущие), а слева от дросселя над самим газом совершают работу силы внешнего давления (поддерживающие стационарность потока). Это учитывается при составлении энергетического баланса в опытах Джоуля — Томсона.

Получим дифференциальное уравнение эффекта Джоуля-Томсона. Для этого запишем функцию состояния - энтальпию в виде: .

Ее дифференциал – полный дифференциал, равный:

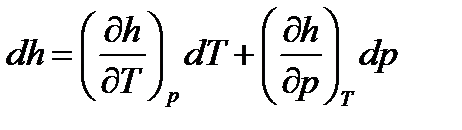. (106)

Удельная теплоемкость при p=const по определению равна:

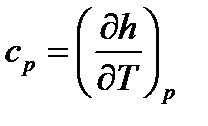. (107)

Производную 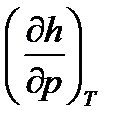, входящую в (1), получим из объединенного выражения 1-го и 2-го законов термодинамики:

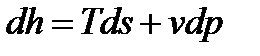. (108)

Разделим уравнение (108) на величину dp при Т=const.

Тогда получим уравнение 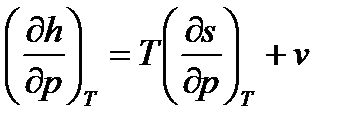, в котором заменим 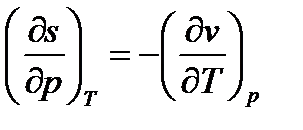, используя уравнения Максвелла (дифференциальные соотношения взаимности). Тогда получим:

. (109)

Подставим в уравнение (106) значения производных 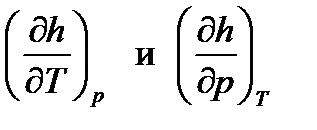из выражений (107) и (109), учитывая, что dh=0:

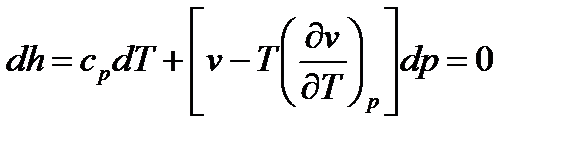, (110)

или при h=const:

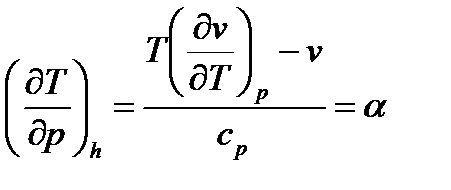. (111)

Уравнение (111) является дифференциальным уравнением эффекта Джоуля-Томсона, которое позволяет определить характер изменения температуры в процессе дросселирования. В уравнении (111) величина называется дифференциальным температурным коэффициентом дросселирования. Для определения величины 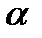требуется знать термическое уравнение состояния и теплоемкость ср для данного вещества.

Поскольку величина dp отрицательна 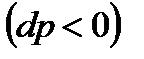, то знак величины dT в уравнении (111) противоположен знаку числителя этого уравнения. Для идеального газа термическое уравнение состояния: pv=RT. Тогда производная 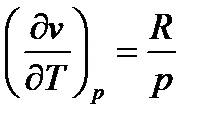и числитель уравнения (111) равен 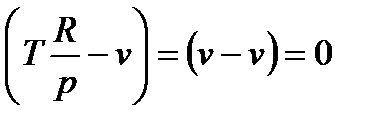, т.е. коэффициент 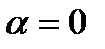. Для реальных газов и паров возможны три случая в зависимости от начального состояния газа перед дросселированием:

1. 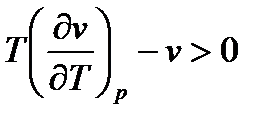. Тогда ;

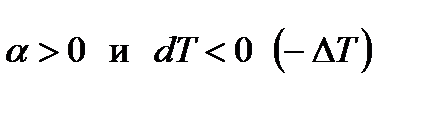2. 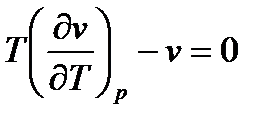. Тогда 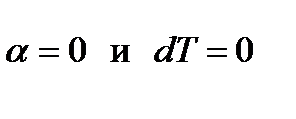- уравнение инверсии;

3. 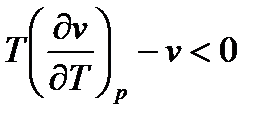. Тогда .

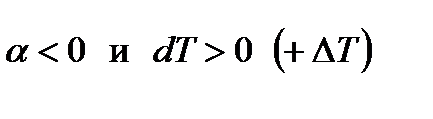Точка, в которой dT=0, есть точка инверсии (перестановки). Температура Т₂=Т₁=Т_инв – температура инверсии. В критической точке для всех веществ 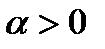и 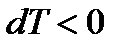, т.е. реализуется 1-ый случай. Проиллюстрируем эти случаи дросселирования с помощью паровой диаграммы T-v для изобары (p=const):

где х – степень сухости пара; tg .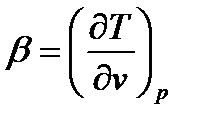

1-ый случай: Если начальное состояние вещества перед дросселированием определяется точкой А, то отрезок на графике MN= 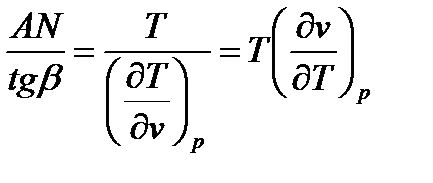является первым слагаемым числителя выражения (6), а отрезок МО=MN-ON= 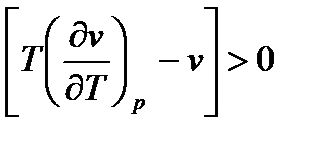является числителем выражения (6), так как MN>ON.

Таким образом, для этого случая и , т.е. газ при дросселировании охлаждается.

2-ой случай: Если начальное состояние перед дросселированием определяется точкой В, то отрезок M1N1<ON1 и М1О=M1N1-ON1 .

Тогда, согласно уравнению (6), 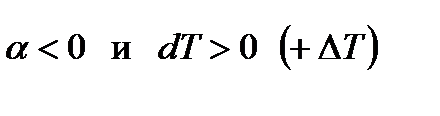и газ при дросселировании нагревается.

3-ий случай: Если начальное состояние вещества перед дросселированием определяется точками С1 и С2,то отрезок М20=0 и согласно уравнению (6), 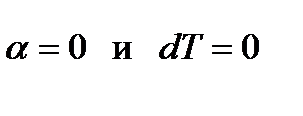, т.е. температура газа не изменяется при дросселировании (точка М2 совпадает с началом координат). Точки С1 и С2 – точки инверсии. Для любой изобары реального газа имеются две точки инверсии С1 и С2, где С1 – в области жидкости и С2 – в области перегретого пара.

Реальный газ или пар можно путем дросселирования перевести в жидкое состояние в том случае, если его начальная температура перед дросселированием будет меньше температуры инверсии Т_инв2. Положительный эффект Джоуля-Томсона используется в холодильной технике для получения холода.

Для идеального газа, молекулы которого рассматриваются как материальные точки, не взаимодействующие между собой, Эффект Джоуля-Томсона равен нулю.

Величина 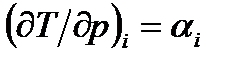- интегральный Эффект Джоуля-Томсона, определяющий изменение температуры при бесконечно малом падении давления в процессе дросселировании.

Выражение

(112)

определяет так называемый интегральный Эффект Джоуля-Томсона (изменение температуры при конечной разности давлений).

Очевидно, что для увеличения интегрального Эффекта Джоуля-Томсона начальную температуру процесса дросселирования нужно понижать.

В зависимости от условий дросселирования один и тот же газ может как нагреваться, так и охлаждаться. Температура, при которой (для данного давления) разность ΔT, проходя через нулевое значение, меняет свой знак, называется температурой инверсии Эффекта Джоуля-Томсона.

При больших перепадах давления на дросселе температура газа может изменяться значительно. Например, при дросселировании от 200 до 1 атмосферы и начальной температуре 17°С воздух охлаждается на 35°С. Этот интегральный эффект положен в основу большинства технических процессов сжижения газов.

2.3.1. Способы задания смесей. Соотношения между массовыми и молярными долями. Определение основных характеристик для смесей. (АЗ: 2, СРС: 1)

Для проведения термодинамических расчетов систем с газовыми смесями или растворами необходимо знать их состав. Состав смеси может быть задан:

- массовыми долями 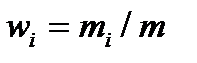, где , где - молярная масса i-го компонента, кг/моль, - относительная молекулярная масса i-го компонента, 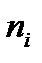- количество i-го компонента, моль;

- молярными долями 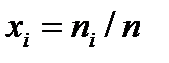, где 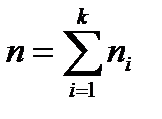, - количество вещества смеси, моль;

- объемными долями, которые равны молярным долям .

Состав смеси идеальных газов может быть также задан парциальными давлениями p_i, массовыми концентрациями ρ и молярными концентрациями .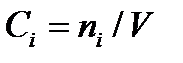

Парциальное давление p_i – это давление i-го компонента газовой смеси при условии, что он занимает весь объем, предназначенный для смеси, при температуре смеси.

На рисунке ниже представлена диаграмма температура – концентрация для двухкомпонентной смеси. По оси абсцисс обычно откладывается концентрация низкокипящего компонента xi (НКК), а по оси ординат температуры низкокипящего компонента (НКК), высококипящего компонента (ВКК) и температуры смеси. Сумма концентраций низкокипящего и высококипящего компонентов в жидкости и паре подчиняется очевидным равенствам

Не нашли, что искали? Воспользуйтесь поиском: