Отличия реальных газов и паров от идеальных. Процессы парообразования. pv-диаграмма водяного пара 4 страница

x1+x2=1; y1+y2=1; (113)

Из термодинамики растворов известен первый закон Коновалова, согласно которому, в состоянии равновесия концентрация низкокипящего компонента в паре выше его концентрации в жидкости. Условием равновесия смесей является равенство температур, давлений и химических потенциалов сосуществующих фаз.

Средняя молярная масса смеси газов определяется выражением , где - масса смеси; где 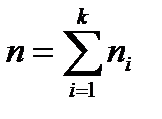, - количество вещества смеси.

Удельная газовая постоянная смеси газов

, Дж/(кг К), где =8.31441, Дж/(моль К) – молярная газовая постоянная; - молярная масса смеси.

Закон Дальтона:

, Па,

т.е. сумма парциальных давлений отдельных газов, входящих в смесь, равна полному давлению смеси.

Для парциального давления и для приведенного объема i-го компонента смеси уравнения имеют вид:

,

.

Тогда, разделив эти уравнения почленно первое на второе, получим

. (114)

2.5.2. Основные характеристики политропных процессов. Уравнения политропного процесса. Соотношения между параметрами в политропном процессе. (АЗ: 2, СРС: 1)

Политропные процессы – это равновесные, обратимые процессы, которые протекают при постоянной теплоемкости c=const. Многие реальные процессы могут быть приближенно описаны уравнениями для политропных процессов.

Каждый политропный термодинамический процесс (ТП) имеет вполне определенный, присущий ему характер распределения энергетических составляющих, входящих в уравнение первого закона термодинамики: , Дж/кг. Это распределение энергетических составляющих будем интерпретировать графически. Например, для процесса V=const имеем:

Штриховка на рисунке означает изменение данной энергетической составляющей, а стрелка – направление ее изменения.

Политропный процесс – это процесс изменения состояния рабочего тела, в котором во внутреннюю энергию в течение всего процесса превращается одна и та же доля количества внешней теплоты:

, Дж/кг, (115)

где .

При этом на совершение внешней механической работы приходится доля теплоты, равная:

, Дж/кг, (116)

где - коэффициент распределения теплоты в политропном процессе.

Теплота, сообщенная газу в бесконечно малом политропном процессе, равна:

, Дж/кг (117)

или для конечного процесса: . (118)

Таким образом, получим теплоемкость политропного процесса: , Дж/кгК.

Зная значение коэффициента в политропном процессе, можно определить теплоемкость c, теплоту q, изменение внутренней энергии и работу расширения (сжатия).

Для вывода уравнения политропного процесса в p-v координатах используем уравнения первого закона термодинамики, выраженные через энтальпию и внутреннюю энергию:

, (119)

, (120)

или

, (121)

. (122)

Отсюда имеем:

, (123)

. (124)

Разделив почленно уравнение (123) на уравнение (124), имеем:

, (125)

где - показатель политропного процесса, который не изменяется в течение всего данного ТП. Из уравнения (125) имеем:

. (126)

Тогда после интегрирования для конечного участка процесса получим:

, (127)

или после потенцирования:

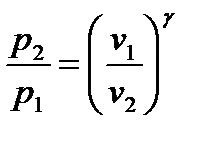, (128)

или . (129)

Это уравнение политропного процесса в координатах p-v. Показатель политропного процесса может иметь любое значение в интервале .

Из выражения (125)можно получить формулу для расчета теплоемкости политропного процесса

, или . (130)

Отсюда имеем , или , (131)

где к=сp/сV – показатель адиабатного процесса. Окончательно имеем:

. (132)

Таким образом, теплоемкость политропного процесса зависит от показателя политропы . Используя термическое уравнение состояния для идеального газа и уравнение (128), можно получить соотношения между параметрами:

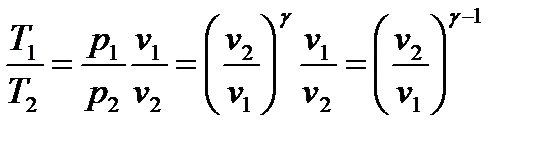. (133)

Учитывая, что , имеем:

. (134)

Расчет функции для политропного процесса. Частные случаи политропных процессов. Графическое представление политропных процессов. (АЗ: 2, СРС: 1)

Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.

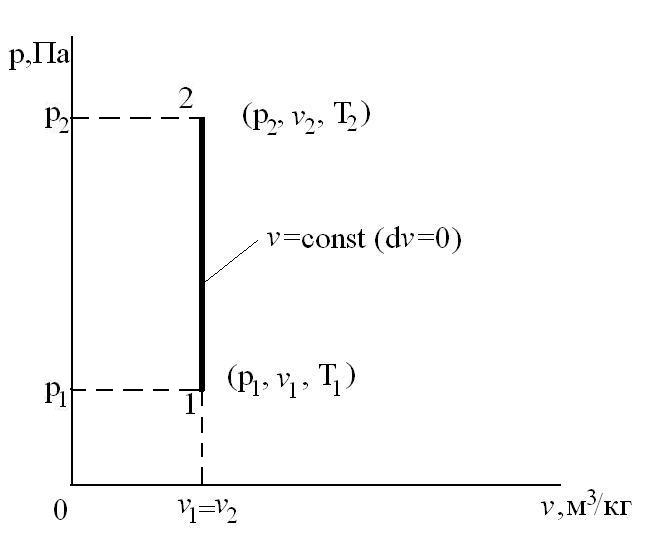
Этот процесс используется как подготовительный процесс в циклах.

Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: , который следует из уравнений состояния для точек 1 и 2: и при .

Поскольку работа расширения в этом процессе равна нулю: , т.к. , то из уравнения 1-го закона термодинамики следует, что:

. (135)

Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП коэффициент распределения теплоты , теплоемкость и показатель политропы:

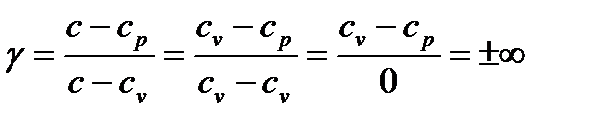. (136)

График распределения энергетических составляющих уравнения 1-го закона термодинамики в изохорном процессе имеет вид:

Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.

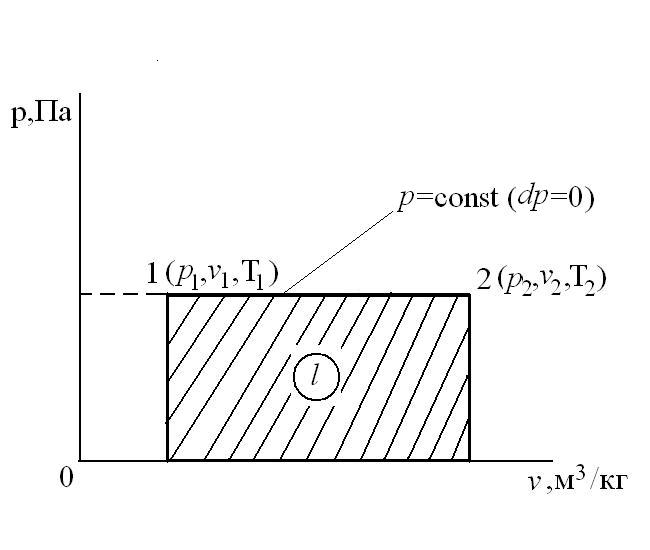
Соотношение между параметрами в процессе р=const: - закон Гей-Люссака, т.к.: , и .

Работа расширения . (137)

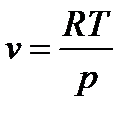Т.к. , то .

Следовательно, удельная газовая постоянная R- это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:

. (138)

Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.

Коэффициент распределения теплоты в процессе р=const равен:

, . (139)

Теплоемкость с=с_р и показатель политропы

. (140)

График распределения энергетических составляющих 1-го закона термодинамики в изобарном процессе имеет вид:

В T-s координатах взаимное положение изобары и изохоры имеет вид:

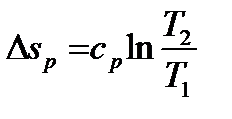, , т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.

Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре

При Т=const из уравнения состояния имеем: - это уравнение изотермического процесса является уравнением равнобокой гиперболы.

Тогда , и - закон Бойля-Мариотта.

Из уравнения 1-го закона термодинамики при имеем:

и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.

Изменение энтальпии в процессе T=const равно:

.

Работа расширения

. (141)

Коэффициент распределения теплоты

. (142)

Тогда теплоемкость и показатель политропы для процесса T=const будет равен , т.е. . (143)

График распределения энергии в процессе T=const имеет вид:

Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и (на конечном и бесконечно малом участке процесса).

Если записать для этого случая уравнения 1-го закона термодинамики в виде:

1. или ,

2. или , то после деления (1) на (2) получим:

- показатель адиабаты.

Тогда после интегрирования выражения для конечного процесса 1-2 будем иметь , или (144)

это есть уравнение адиабатного процесса в p-v-координатах, которое является уравнением неравнобокой гиперболы.

, т.к. Т , то ds=0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.

Соотношения между параметрами состояния в этом процессе:

и , (145)

а график распределения энергии в процессе имеет вид:

Из уравнения 1-го закона термодинамики следует, что , т.е. . Таким образом, работа расширения в адиабатном процессе совершается за счет уменьшения внутренней энергии газа, а его температура уменьшается .

Работа расширения по аналогии с политропным процессом будет равна:

, (146)

или . (147)

Коэффициент распределения теплоты в процессе q=0:

, а теплоемкость адиабатного процесса .

Показатель адиабаты для одноатомных газов равен к=1,66, для двухатомных к=1,4 и для трехатомных к=1,3.

Все политропные процессы можно разделить на три группы:

- I группа – политропы, показатель которых изменяется в пределах , а теплотa q в процессе подводится к рабочему телу (+q);

- II группа – политропы, показатели которых лежат в пределах , с подводом теплоты к рабочему телу (+q);

- III группа – политропы, показатели которых лежат в пределах с отводом теплоты от системы в холодильник (-q).

Взаимное положение групп политроп в p-v координатах имеет вид:

Взаимное положение групп политроп в T-s координатах имеет вид:

У каждой из групп политроп имеется свой собственный закон распределения энергетических составляющих уравнения 1-го закона термодинамики и собственное значение показателя политропы .

I группа

При расширении газа с ростом ослабевает роль источника теплоты и увеличивается роль внутренней энергии в производстве механической работы.

II группа ()

При расширении газа с ростом увеличивается доля теплоты, идущей на работу, и уменьшается доля теплоты, идущей на нагрев газа.

III группа ()

При расширении газа с ростом уменьшается доля внутренней энергии, идущей на работу, и увеличивается доля внутренней энергии, отдаваемая холодильнику.

2.10.1. Классификация и схемы компрессоров. Расчет затрат на сжатие газа в одноступенчатых и много ступенчатых компрессорах (АЗ: 2, СРС: 2)

Тепловые машины подразделяются на тепловые двигатели и тепловые трансформаторы, к которым относятся холодильные установки и тепловые насосы. В тепловых двигателях происходит превращение теплоты в работы. Тепловые трансформаторы переносят тепловую энергию от холодных тел к горячим телам при затрате работы. На следующей схеме показано направление переноса теплоты от холодного тела к горячему телу при затрате работы в холодильной установке и тепловом насосе.

Окружающая среда является горячим телом в холодильных установках и холодным телом в тепловых насосах.

Тепловые машины используют в качестве рабочего тела либо газ, либо пар, которые изменяют свои параметры при изменении своего состояния по циклу.

Циклы тепловых двигателей – прямые циклы, требующие для своего осуществления затраты теплоты. В них линия расширения лежит выше линии сжатия в p-v координатах, т.е. прямые циклы направлены по часовой стрелке, как показано на рисунке

Циклы трансформаторов - обратные циклы, направленные против часовой стрелки в p-v координатах.

Циклы бывают замкнутые и разомкнутые. Циклы двигателей внутреннего сгорания (ДВС) поршневых и реактивных двигателей являются разомкнутыми циклами. При термодинамических расчетах ДВС методом круговых процессов разомкнутые циклы этих двигателей условно рассматриваются как замкнутые циклы. Тепловые двигатели, работающие по замкнутому циклу, являются двигателями внешнего сгорания. Примером двигателя внешнего сгорания является двигатель Стирлинга, в котором рабочее тело (гелий или водород) постоянно находится в замкнутом пространстве и изменяет свой объем при нагревании и охлаждении, а теплота образуется вне этого замкнутого пространства. Этот двигатель разработан Р.Стирлингом в 1816г. в Великобритании.

Принципиальная схема тепловой машины, работающей по замкнутому циклу, имеет вид:

Для кругового процесса du=0 и . Для теплового двигателя q₁ есть сумма теплот, подведенных за цикл к термодинамическому рабочему телу (ТРТ) от источника, а q₂ – сумма теплот, отведенных за цикл от ТРТ в холодильник. Результирующая работа двигателя за цикл - совершается за счет разности теплот .

Для теплового трансформатора:

q₁ - есть теплота, отводимая от ТРТ к горячему телу;

q₂ – теплота, подводимая от холодного тела к ТРТ;

l_ц<0 – работа, затрачиваемая ТС на перенос тепловой энергии от холодного тела к горячему телу;

-l_ц=-q₁+q2, или q₁=l_ц+q₂.

Компрессоры предназначаются для сжатия газообразных рабочих тел. На осуществление обратного цикла, по схеме которого работают компрессоры, расходуется механическая работа.

Одноступенчатый компрессор

Давление р₃=р₂ и температура Т₃=Т₁.

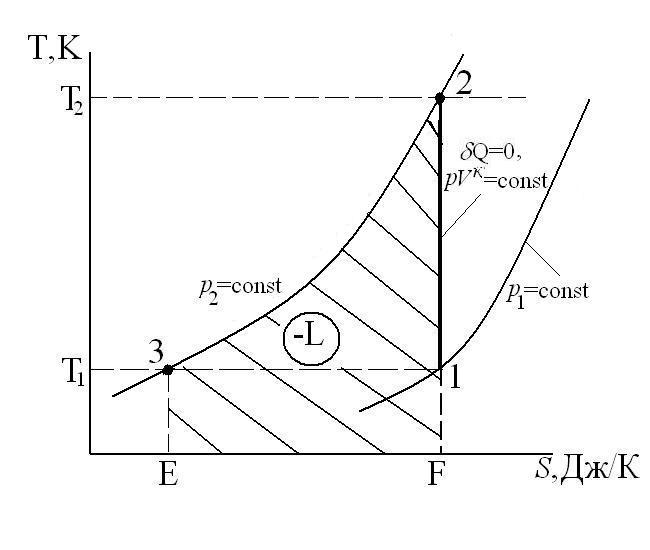
Процесс сжатия в компрессоре в p-v и T-s координатах имеет вид:

где А-1 – линия всасывания; 1-2 – процесс сжатия газа; 2-В – линия нагнетания сжатого газа в баллон; (-L) – работа, затрачиваемая на привод компрессора.

На диаграмме T-s работа, затрачиваемая на привод компрессора равна площади F23EF.

Линия А-1 и 2-В не изображают термодинамические процессы в координатах р[Па]-V[м3], так как количество рабочего тела на них переменно. При этом удельные параметры состояния газа (p, v, T) практически не изменяются. Основной характеристикой компрессора является степень повышения давления П=р2/р1. Для одноступенчатого компрессора П=8-12. Величина П=р2/р1 для одноступенчатого компрессора ограничивается максимальной температурой в конце процесса сжатия Т2max (3000C) из-за опасности возгорания масла и наличием вредного (мертвого) пространства между поршнем компрессора и днищем цилиндра из-за размещения в нем клапанов (всасывающего и нагнетательного), что учитывается объемным кпд компрессора , где V – фактический объем всасываемого газа. Для реальных компрессоров (всегда). Влияние вредного пространства на степень повышения давления в одноступенчатом компрессоре проиллюстрируем следующим рисунком:

где процесс В1-А1 – это процесс расширения газа, оставшегося во вредном пространстве; т.А1 – фактическое начало всасывания газа. С ростом давления р2 объемный кпд компрессора уменьшается и при фактический объем всасываемого газа равен нулю () и .

При расчете работы на привод компрессора принимается, что процесс сжатия газа – равновесный, вредное пространство отсутствует и потерями давления на всасывание и нагнетание газа можно пренебречь. Тогда цикл компрессора будет иметь вид:

Механическая работа, затрачиваемая в одноступенчатом компрессоре на сжатие 1 кг газа, равна:

, (148)

или , (149)

или , (150)

где показатель политропы .

При медленном сжатии (изотерма). При очень быстром сжатии (адиабата). Работа при адиабатном сжатии равна

. (151)

При изотермическом сжатии работа равна:

. (152)

Сжатие в многоступенчатом компрессоре

При расчете работы на привод многоступенчатого компрессора принимается, что Т2=Т , т.е. что температура газа в конце процесса сжатия в каждой ступени одинакова, и что работа сжатия в каждой из ступеней компрессора одинакова, т.е. l₁=l₂=l₃=l_ц/3, где 3 – число ступеней компрессора в рассматриваемом примере. Каждая ступень работает в одном и том же интервале температур от Т₁ до Т₂, как показано на следующей схеме:

При этом в каждой ступени имеет место один и тот же политропический процесс сжатия:

, и т.д., (153)

где П₁=П₂=П₃=П. Тогда р₂=П_р1, р =П_2р1, р =П_3р1 и т.д.

При этом конечное давление в многоступенчатом компрессоре с числом ступеней N будет равно:

.

Тогда для трехступенчатого компрессора (N=3) работа, затраченная на сжатие газа, будет равна:

, (154)

а для произвольного числа ступеней N будем иметь следующее выражение:

. (155)

Не нашли, что искали? Воспользуйтесь поиском: