Излучение абсолютно чёрного тела

Вследствие линейности уравнений электромагнитного поля любое их решение может быть представлено в виде суперпозиции монохроматических волн, каждая с определённой частотой . Энергия поля может быть представлена как сумма энергий соответствующих полевых осцилляторов. Как известно из квантовой механики, энергия осциллятора принимает дискретные значения согласно следующей формуле:

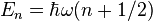
Поскольку рассматривается равновесное излучение, то, используя каноническое распределение Гиббса, можно определить вероятность состояния осциллятора с заданной энергией:

Статистическая сумма равна

Свободная энергия равна

Для средней (математическое ожидание) энергии воспользуемся уравнением Гиббса — Гельмгольца

Таким образом средняя энергия, приходящаяся на полевой осциллятор равна

(1)

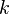где — постоянная Планка, — постоянная Больцмана.

Количество же стоячих волн в единице объёма в трёхмерном пространстве в интервале от равно^[1][2]:

(2)

Следовательно, для спектральной плотности мощности электромагнитного излучения получаем

Первое слагаемое в этой формуле связано с энергией нулевых колебаний, второе — это и есть формула Планка.

Формулу Планка также можно записать и через длину волны:

(5)

Не нашли, что искали? Воспользуйтесь поиском: