
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Способах задания её движения
Траекторией точки называется геометрическое место последовательных положений этой точки в пространстве.
Существует три способа задания движения точки: векторный, координатный и естественный.
При векторном способе задания движения положение точки М определяется заданием радиуса-вектора  , проведенного из некоторого заданного центра О (рис. 1):
, проведенного из некоторого заданного центра О (рис. 1):

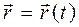 . (1.1)
. (1.1)
Выражение (1.1) является законом движения при векторном способе. Скорость точки равна первой производной от радиус-вектора точки по времени
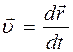 . (1.2)
. (1.2)
Вектор скорости 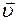 направлен по касательной к траектории в сторону движения точки.
направлен по касательной к траектории в сторону движения точки.
Ускорение точки равно первой производной от вектора скорости по времени или второй производной от радиус-вектора по времени
 . (1.3)
. (1.3)
Вектор ускорения 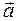 лежит в соприкасающейся плоскости траектории и направлен в сторону её вогнутости.
лежит в соприкасающейся плоскости траектории и направлен в сторону её вогнутости.
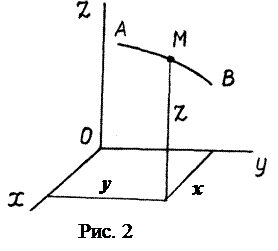
При координатном способе задания движения положение точки М в системе отсчёта Оxyz определяется тремя координатами x, y, z. При движении точки её координаты изменяются с течением времени, следовательно, они являются функциями от времени (рис. 2)
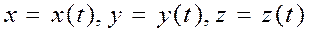 . (1.4)
. (1.4)
|
 определяются проекции скорости на оси координат как первые производные от соответствующих координат точки по времени
определяются проекции скорости на оси координат как первые производные от соответствующих координат точки по времени
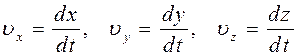 . (1.5)
. (1.5)
 После вычисления проекций скоростей определяются модуль и направление вектора скорости
После вычисления проекций скоростей определяются модуль и направление вектора скорости 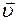 точки
точки
 , (1.6)
, (1.6)
и направляющие косинусы вектора 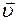
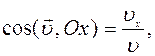
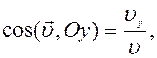
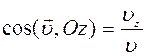 . (1.7)
. (1.7)
Скорость точки измеряется в м/с.
Проекции ускорения на оси координат равны первым производным от соответствующих проекций скорости по времени или вторым производным от соответствующих координат точки по времени
 . (1.8)
. (1.8)
Вычислив проекции ускорения на оси координат, можно определить модуль и направление вектора ускорения 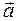 точки:
точки:
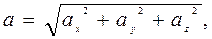 (1.9)
(1.9)

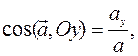
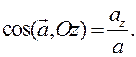 (1.10)
(1.10)
Ускорение точки измеряется в м/с2.
При естественном способе задания движения точки известны (рис. 3):
1. Траектория точки АВ.
2. Начало отсчёта О с указанием положительного «+» и отрицательного «-» направлений отсчёта дуговой координаты 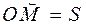 .
.
3. Закон изменения дуговой координаты  .
.
Выражение  является законом движения при естественном способе задания движения точки.
является законом движения при естественном способе задания движения точки.
Модуль скорости при естественном способе равен первой производной от дуговой координаты S по времени
 . (1.11)
. (1.11)
 Если
Если  , то вектор
, то вектор 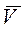 направляем в сторону положительного отсчёта дуговой координаты S, если
направляем в сторону положительного отсчёта дуговой координаты S, если 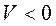 , то – в противоположную сторону.
, то – в противоположную сторону.
Вектор ускорения 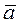 при естественном способе предстаёт как геометрическая сумма векторов касательного
при естественном способе предстаёт как геометрическая сумма векторов касательного 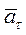 и нормального
и нормального 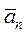 ускорений
ускорений
 . (1.12)
. (1.12)
Касательное ускорение 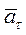 есть составляющая вектора ускорения, которая получается проектированием вектора
есть составляющая вектора ускорения, которая получается проектированием вектора 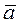 на касательную к траектории в точке
на касательную к траектории в точке 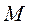 . Касательное ускорение
. Касательное ускорение 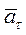 характеризует изменение модуля вектора скорости
характеризует изменение модуля вектора скорости 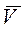 во времени. Модуль касательного ускорения равен первой производной от скорости точки
во времени. Модуль касательного ускорения равен первой производной от скорости точки 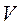 по времени или второй производной от дуговой координаты
по времени или второй производной от дуговой координаты 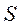 по времени
по времени
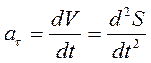 . (1.13)
. (1.13)
Если 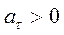 , то вектор
, то вектор 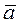 направляется в сторону положительного отсчёта дуговой координаты S, если
направляется в сторону положительного отсчёта дуговой координаты S, если  , то – в противоположную сторону.
, то – в противоположную сторону.
Нормальное ускорение 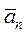 есть составляющая вектора ускорения, которая получается путём проектирования вектора
есть составляющая вектора ускорения, которая получается путём проектирования вектора 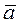 на направление главной нормали траектории в точке
на направление главной нормали траектории в точке 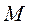 . Нормальное ускорение
. Нормальное ускорение 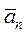 характеризует изменение вектора скорости
характеризует изменение вектора скорости 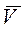 по направлению. Модуль нормального ускорения равен
по направлению. Модуль нормального ускорения равен
 , (1.14)
, (1.14)
где 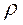 – радиус кривизны траектории в точке M.
– радиус кривизны траектории в точке M.
Вектор нормального ускорения 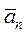 направлен всегда к центру кривизны траектории.
направлен всегда к центру кривизны траектории.
Учитывая, что  , модуль ускорения точки:
, модуль ускорения точки:
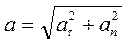 . (1.15)
. (1.15)
Рассмотрим частные случаи движения точки:
1. Равномерное прямолинейное движение. В этом случае 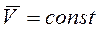 .
.
Тогда касательное ускорение
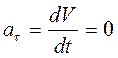 , так как
, так как  ;
;
нормальное ускорение
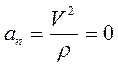 ,
,
так как радиус кривизны прямолинейной траектории 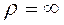 . Значит, согласно выражению (1.15), ускорение точки
. Значит, согласно выражению (1.15), ускорение точки 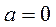 .
.
Учитывая, что 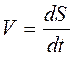 ,
, 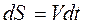 .
.
После интегрирования 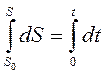 ,
,
получаем
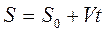 . (1.16)
. (1.16)
Выражение (1.16) является законом движения точки в рассматриваемом случае.
2. Равномерное криволинейное движение. В этом случае  .
.
Тогда 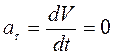 ;
; 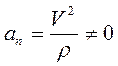 .
.
Ускорение точки  , т.е. по модулю и направлению совпадает с нормальным ускорением
, т.е. по модулю и направлению совпадает с нормальным ускорением 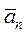 . Закон движения точки по траектории в этом случае определяется выражением (1.16).
. Закон движения точки по траектории в этом случае определяется выражением (1.16).
3. Равнопеременное прямолинейное движение. В этом случае 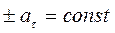 (знак «+» соответствует ускоренному движению точки, знак «–» соответствует замедленному движению).
(знак «+» соответствует ускоренному движению точки, знак «–» соответствует замедленному движению).
Учитывая, что 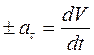 ,
, 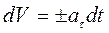 .
.
После интегрирования  получается
получается
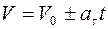 , (1.17)
, (1.17)
где 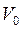 – скорость при
– скорость при  . Выражение (1.17) определяет закон изменения скорости в этом случае.
. Выражение (1.17) определяет закон изменения скорости в этом случае.
В рассматриваемом случае нормальное ускорение
 , так как
, так как 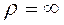 .
.
В этом случае ускорение точки  , т.е. по модулю и направлению совпадает с касательным ускорением
, т.е. по модулю и направлению совпадает с касательным ускорением 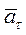 . После повторного интегрирования (1.17) получается выражение, которое описывает закон движения в этом случае
. После повторного интегрирования (1.17) получается выражение, которое описывает закон движения в этом случае
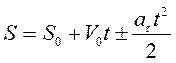 . (1.18)
. (1.18)
4. Равнопеременное криволинейное движение. В этом случае, в отличие от рассмотренного в п. 3, 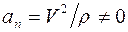 , ускорение
, ускорение 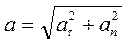 . Закон изменения скорости и закон движения точки определяется соответственно выражениями (1.17) и (1.18).
. Закон изменения скорости и закон движения точки определяется соответственно выражениями (1.17) и (1.18).
5. Общий случай движения. В этом случае 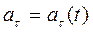 . Тогда закон изменения скорости определяется выражением
. Тогда закон изменения скорости определяется выражением
 . (1.19)
. (1.19)
Закон движения точки
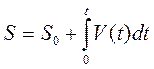 . (1.20)
. (1.20)
Рассмотрим переход от координатного способа к естественному. Пусть движения точки заданы координатным способом, т.е. известны функции (1.4). Найдем закон движения 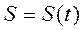 . Дифференциал дуги равен
. Дифференциал дуги равен
 (1.21)
(1.21)
где  ,
, 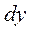 ,
, 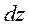 – дифференциалы координат точки:
– дифференциалы координат точки:  ,
, 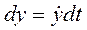 ,
,  .
.
Подставляем значения и интегрируем выражение (1.21)
 .
.
Окончательно получаем
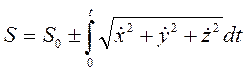 , (1.22)
, (1.22)
где S 0 – дуговая координата при 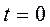 .
.
Введём понятие о годографе скорости точки.
Точка  , двигаясь по криволинейнойтраектории
, двигаясь по криволинейнойтраектории 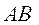 (рис. 4), занимаетна ней последовательные положения
(рис. 4), занимаетна ней последовательные положения 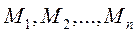 . Скорость точки в этих положениях равна соответственно
. Скорость точки в этих положениях равна соответственно 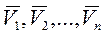 .
.
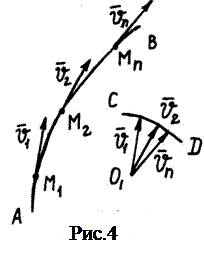 Выбираем в пространстве некоторую точку
Выбираем в пространстве некоторую точку 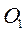 и откладываем от этой точки векторы, геометрически равные скоростям
и откладываем от этой точки векторы, геометрически равные скоростям 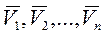 . Если от точки
. Если от точки 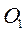 отложить векторы скорости, соответствующие всем положениям точки
отложить векторы скорости, соответствующие всем положениям точки 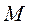 на траектории
на траектории 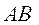 , и соединить концы этих векторов, то получится линия CD, которая является годографом скорости. Таким образом, годограф скорости представляет собой геометрическое место, где находятся концы векторов скорости движущейся точки, отложенных от одной и той же точки пространства.
, и соединить концы этих векторов, то получится линия CD, которая является годографом скорости. Таким образом, годограф скорости представляет собой геометрическое место, где находятся концы векторов скорости движущейся точки, отложенных от одной и той же точки пространства.
Если точку 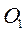 , от которой откладываются скорости движущейся точки, совместить с началом отсчёта системы координат
, от которой откладываются скорости движущейся точки, совместить с началом отсчёта системы координат 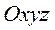 , то уравнения
, то уравнения
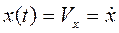 ,
, 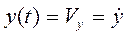 ,
, 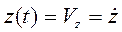 (1.23)
(1.23)
являются параметрическими уравнениями годографа скорости.
В главе «Кинематика точки» можно выделить два основных класса задач:
- определение уравнений движения точки, её траектории, а также скорости, ускорения и радиуса кривизны траектории в заданный момент времени;
- частные случаи движения точки.
Первый класс задач рассмотрим на следующем примере.
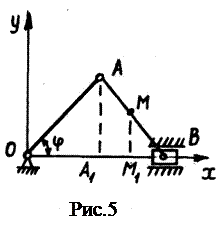 Пример 1. Кривошип
Пример 1. Кривошип 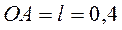 м кривошипно-ползунного механизма (рис. 5) вращается вокруг оси
м кривошипно-ползунного механизма (рис. 5) вращается вокруг оси  по закону
по закону 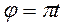 (
(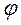 – в радианах,
– в радианах, 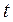 – в секундах). Для точки
– в секундах). Для точки 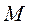 шатуна
шатуна 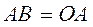 и
и 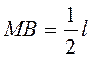 :
:
1. Найти уравнения движения в системе координат 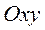 .
.
Для определения уравнений движения точки 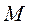 выбираем произвольное положение механизма (когда
выбираем произвольное положение механизма (когда  и
и  ) в системе отсчёта
) в системе отсчёта 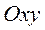 и выражаем координаты точки
и выражаем координаты точки 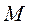 шатуна
шатуна
 ,
, 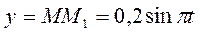 ,
,
где 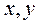 – выражены в метрах.
– выражены в метрах.
2. Определить траекторию точки, построить траекторию и указать положение точки 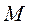 на траектории при
на траектории при 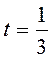 с.
с.
Для определения траектории точки 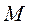 необходимо из полученных уравнений движения
необходимо из полученных уравнений движения 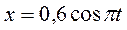 ,
, 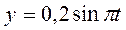 исключить параметр времени
исключить параметр времени 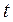 . В рассматриваемом случае это можно сделать следующим образом. Перепишем уравнения движения
. В рассматриваемом случае это можно сделать следующим образом. Перепишем уравнения движения
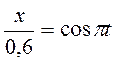 ;
; 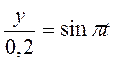 .
.
Возводя в квадрат эти выражения и складывая, получим уравнение траектории точки:
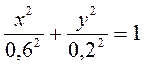 .
.
 Таким образом, траектория точки
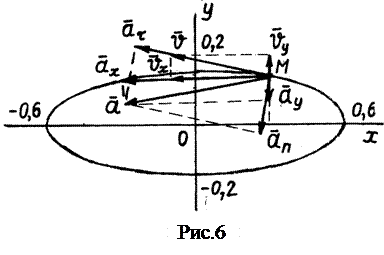
Таким образом, траектория точки  представляет собой эллипс с полуосями a = 0,6 м, b = 0,2 м (рис. 6).
представляет собой эллипс с полуосями a = 0,6 м, b = 0,2 м (рис. 6).
Находим положение точки  при
при 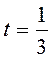 с. Для этого в полученные уравнения движения подставляем заданное время
с. Для этого в полученные уравнения движения подставляем заданное время
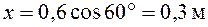 ,
, 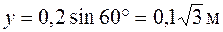 .
.
Указываем точку  на траектории.
на траектории.
3. Для момента времени 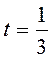 с найти скорость точки и построить вектор скорости
с найти скорость точки и построить вектор скорости 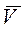 .
.
Определяем проекции скорости точки 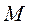 на оси координат
на оси координат
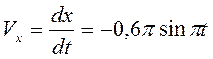 ,
,  .
.
При 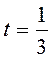 с
с 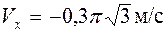 ;
;  .
.
Скорость точки 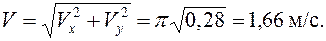
Зная проекции скорости 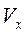 и
и 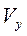 при
при 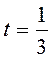 с, строим вектор
с, строим вектор 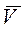 на рис. 6. Вектор
на рис. 6. Вектор 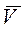 направлен по касательной к траектории в точке
направлен по касательной к траектории в точке 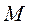 .
.
4. Для момента времени 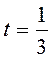 с найти ускорение точки и построить вектор
с найти ускорение точки и построить вектор 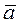 на рисунке.
на рисунке.
Определяем проекции ускорения точки 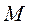 на оси координат
на оси координат
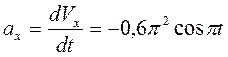 ,
, 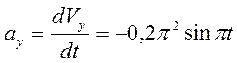 .
.
При  с
с  м/с²,
м/с²,  .
.
Ускорение точки 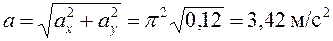 .
.
Зная проекции ускорения  и
и  , строим вектор ускорения
, строим вектор ускорения 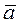 .
.
5. В момент времени 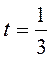 с найти радиус кривизны траектории
с найти радиус кривизны траектории 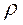 , нормальное an и касательное aτ ускорения точки.
, нормальное an и касательное aτ ускорения точки.
Радиус кривизны определяем из выражения для нормального ускорения 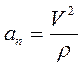 , откуда
, откуда 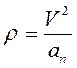 .
.
Нормальное ускорение
 ,
,
где касательное ускорение
 .
.
При 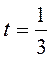 с
с
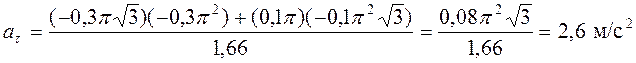 .
.
Находим нормальное ускорение
 .
.
Тогда радиус кривизны траектории
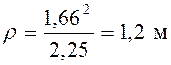 .
.
Покажем на рис. 6 векторы касательного ускорения 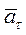 , спроектировав ускорение
, спроектировав ускорение 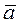 на направление касательной, и нормального ускорения
на направление касательной, и нормального ускорения 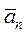 , спроектировав
, спроектировав 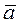 на направление нормали.
на направление нормали.
Методику решения задач на частные случаи движения точки рассмотрим на следующих двух примерах.
Пример 2. Точка начинает двигаться равноускоренно из состояния покоя по окружности радиусом R = 0,5 м и за первые 5 с проходит путь, равный 2 м. Определить закон движения точки по окружности, приняв за начало отсчёта начальное положение точки, а также её скорость и ускорение в конце 5 с.
Для решения задачи записываем выражения, по которым определяются скорость и закон движения точки при равноускоренном движении:
 ;
; 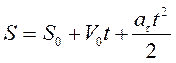 .
.
По условию данной задачи 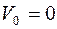 ,
, 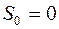 .
.
Отсюда  ,
, 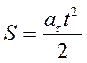 .
.
При 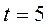 с
с 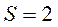 м. Тогда
м. Тогда 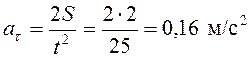 .
.
Скорость точки при 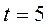 с равна
с равна 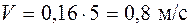 .
.
Находим нормальное ускорение точки
 .
.
Ускорение точки при 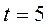 с равно
с равно
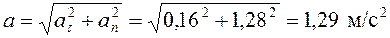 .
.
Пример 3. Точка движется так, что её касательное ускорение 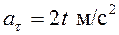 . Определить закон её движения, если при
. Определить закон её движения, если при 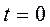 ,
, 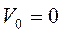 и
и 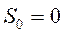 .
.
Касательное ускорение  , откуда
, откуда 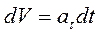 .
.
Интегрируем данное выражение
 .
.
Отсюда 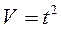 (м/с).
(м/с).
С другой стороны, 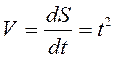 . Значит,
. Значит,  .
.
Интегрируя данное выражение, получаем:
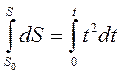 .
.
Закон движения точки в данном примере 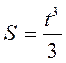 (м).
(м).
Примечание. Дуговую координату 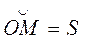 (рис. 3) не следует путать с проходимым точкой расстоянием. Путь
(рис. 3) не следует путать с проходимым точкой расстоянием. Путь  за время
за время 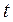 есть величина всегда положительная и равная сумме проходимых точкой отрезков за данный промежуток времени, в то время как координата
есть величина всегда положительная и равная сумме проходимых точкой отрезков за данный промежуток времени, в то время как координата 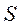 , характеризующая положение точки на траектории, может быть в данный момент времени и отрицательной. Это отличие видно из следующего примера.
, характеризующая положение точки на траектории, может быть в данный момент времени и отрицательной. Это отличие видно из следующего примера.
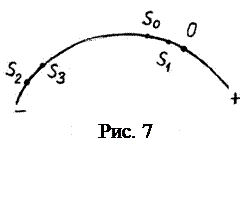
Пример 4. Точка 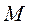 (рис. 7) движется по некоторой криволинейной траектории согласно закону
(рис. 7) движется по некоторой криволинейной траектории согласно закону 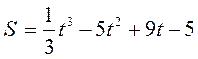 ,
, 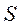 – в метрах,
– в метрах, 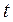 – в секундах. Определить путь
– в секундах. Определить путь 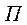 , пройденный точкой за время
, пройденный точкой за время 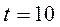 с.
с.
Находим моменты времени остановки точки
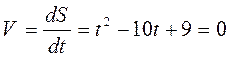 .
.
 Корни полученного квадратного уравнения
Корни полученного квадратного уравнения
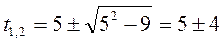 ;
;
 с;
с;
 с.
с.
Находим положения точки на траектории в моменты времени
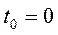 ,
, 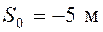 ;
;
 с,
с, 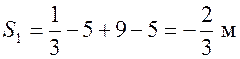 ;
;
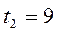 с,
с,  ;
;
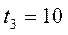 с,
с, 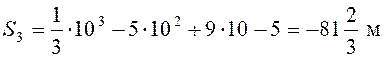 .
.
Путь за время 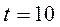 с равен сумме криволинейных отрезков
с равен сумме криволинейных отрезков
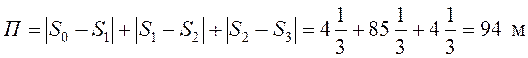 .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как задаётся движение точки при векторном, координатном и естественном способах?
2. Что называется траекторией точки?
3. Как определяется скорость точки при векторном, координатном и естественном способах задания движения?
4. Как определяется ускорение точки при векторном, координатном и естественном способах задания движения?
5. Что называется годографом скорости точки?
Не нашли, что искали? Воспользуйтесь поиском: