Центр тяжести твёрдого тела

Тело А (рис. 64) находится в однородном поле сил тяготения. Разбиваем это тело на бесконечно малые тела 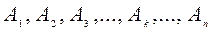, вес которых соответственно равен 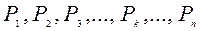. Отсюда следует, что на тело действует система параллельных сил. Равнодействующая этой системы сил есть вес тела

.

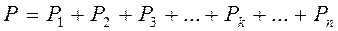Точка С, в которой приложен вес тела , называется центром тяжести тела.

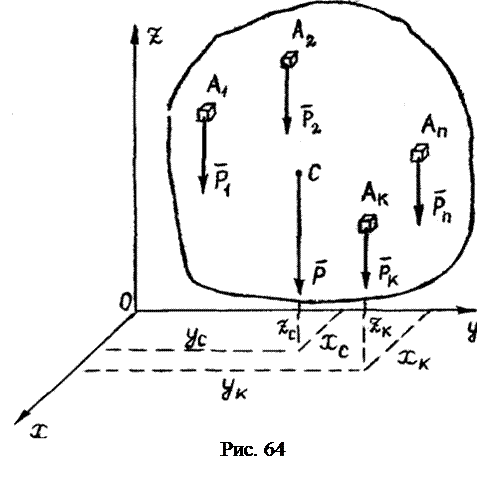
Согласно основному свойству центра параллельных сил, положение центра тяжести С относительно тела А не меняется при повороте тела в пространстве.

Следовательно, центром тяжести тела называется точка С, в которой приложен вес тела Р и положение которой относительно тела не меняется при повороте тела в пространстве.

Координаты центра тяжести С найдём, используя выражения (4.6) для координат центра параллельных сил:

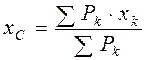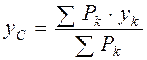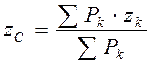, , . (4.7)

В общем случае для определения координат центра тяжести тела используют выражения (4.7). Однако если тела однородные, то эти выражения можно упростить.

Однородный объём

Обозначим через 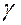вес единицы объёма тела (удельный вес).

Тогда вес k -го элемента тела с объёмом 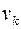равен 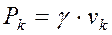. Вес тела объёмом V равен

.

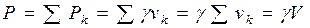Подставляя значения Р, Р_К в выражения (4.7), получаем координаты центра тяжести однородного объёма:

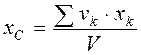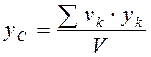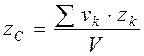, , , (4.8)

где 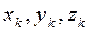– координаты центра тяжести k -го тела объёмом .

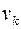Если тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то разбиваем тело на бесконечно малые объёмы 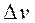и, переходя в выражениях (4.8) к пределу при 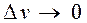, получаем выражение (4.9):

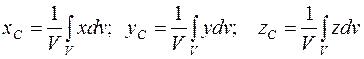. (4.9)

В выражениях (4.9) интегрирование осуществляется по всему объёму V.

Однородная площадь

Совмещаем тело с плоскостью Oxy. В этом случае координата центра тяжести тела .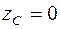

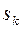Пусть – вес единицы площади тела. Вес k -го элемента тела площадью равен 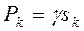, вес тела площадью S равен

.

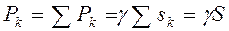Подставляя 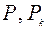в выражения (4.7), получаем координаты центра тяжести однородного плоского тела:

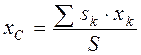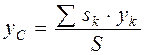, . (4.10)

Из выражений (4.10) получаем

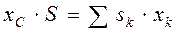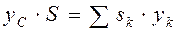, . (4.11)

Выражения (4.11) называются статическими моментами площади относительно осей Oy и Ox соответственно. Если начало отсчёта О системы осей Oxy совместить с центром тяжести – точкой С, то в этом случае координаты центра тяжести тела 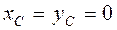. Из выражений (4.11) следует, что в этом случае статические моменты тела равны 0:

, .

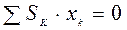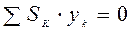Следовательно, статический момент площади относительно любой оси, проходящей через центр тяжести тела, равен нулю.

Если плоское тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) получаются выражения интегрального вида:

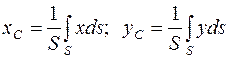. (4.12)

В выражениях (4.12) интегрирование проводится по площади тела S.

Однородная линия

Разбиваем тело на ряд тел, координаты центров тяжести из­вестны. Обозначим через 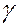вес единицы длины тела. Тогда вес 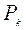тела длиной l_k равен 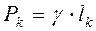, вес тела длиной L равен

.

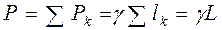Подставляя значения 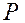, 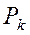в выражения (4.7), получаем после сокращения на 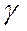координаты центров тяжести однородной линии:

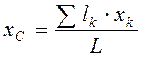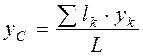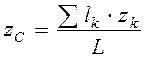, , . (4.13)

Если линия не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) и (4.12) получаются интегральные выражения:

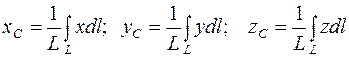. (4.14)

В выражениях (4.14) интегрирование осуществляется по всей длине линии L, т.е. это криволинейные интегралы.

Не нашли, что искали? Воспользуйтесь поиском: