Гармонические колебания. Рассмотрим движение пружинного маятника — материальной точки массой т, подвешенной на пружине с жесткостью k

Рассмотрим движение пружинного маятника — материальной точки массой т, подвешенной на пружине с жесткостью k. Если пружину оттянуть (сжать) на расстояние к от положения равновесия, то возникнет дополнительная упругая сила, величина и направление которой определяются законом Гука:

F = — k·x. (10.1)

Знак «—» показывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т. е. к положению равновесия.

Предположим, что силы сопротивления отсутствуют. Тогда, подставив выражение (10.1) в формулу второго закона Ньютона, получим дифференциальное уравнение свободных колебаний при отсутствии трения:

Преобразуем выражение (10.2) следующим образом: Отношение положительно, поэтому целесообразно заменить его квадратом некоторой величины:

Получили дифференциальное уравнение второго порядка:

Его решение приводит к гармоническому закону:

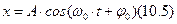
где А — амплитуда колебаний,

ω₀ — собственная круговая (циклическая) частота колебаний,

φ= (φ₀t + φ₀) — фаза колебаний,

φ₀—начальная фаза колебаний (при t = 0).

Амплитуда и начальная фаза колебаний определяются начальными условиями движения, т. е. положением и скоростью материальной точки в момент времени t = 0.

Гармоническими колебаниями называются колебания, при которых наблюдаемая величина изменяется во времени по закону синуса или косинуса.

Таким образом, пружинный маятник совершает гармонические колебания.

График зависимости смещения от времени при гармонических колебаниях для случая φ₀ = 0 представлен на рис. 10.2.

Наряду с круговой частотой ω₀используют и другие характеристики колебательного движения:

• частота колебаний v, равная числу колебаний, совершаемых за единицу времени:

v= (10.6)

• период колебаний Т, равный времени, в течение которого совершается одно полное колебание:

Рис. 10.2. График зависимости смещения от времени при гармонических колебаниях

Связь между указанными характеристиками определяется формулами:

Закон движения (10.5) позволяет определить скорость и ускорение колеблющегося тела в любой момент времени:

где v_max = А·ω₀ — максимальная скорость (амплитуда скорости);

где а_mах = A∙ω₀²— максимальное ускорение (амплитуда ускорения).

Колеблющаяся материальная точка в любой момент времени обладает кинетической энергией собственного движения — Е_к и потенциальной энергией E _п, связанной с деформацией пружины.

Полная энергия колеблющегося тела складывается из его кинетической и потенциальной энергий:

Как видно из (10.12), в этом случае полная механическая энергия системы не изменяется.

Не нашли, что искали? Воспользуйтесь поиском: