Затухающие колебания

Учет сил трения и сопротивления в реальных системах существенно изменяет характер движения: энергия движения постоянно убывает и колебания либо становятся затухающими, либо колебательное движение вообще не возникает.

Если в рассматриваемой системе появляются силы сопротивления среды (силы трения), то второй закон Ньютона можно записать так:

Предполагают, что при не очень больших амплитудах и частотах сила сопротивления пропорциональна скорости движения и, естественно, направлена противоположно ей:

где r — коэффициент трения, характеризующий свойства среды оказывать сопротивление движению. Учитывая (10.13) и (10.14),

или

где

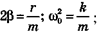β─коэффициент затухания; ω₀ - круговая частота собственных колебаний системы.

Решение полученного дифференциального уравнения зависит от знака разности ω²= ω₀²— β², т. е. от соотношения между величинами β и ω₀. Параметр есть круговая частота затухающих колебаний.

а) Если ω₀²— β²> 0 и круговая частота со является действительной величиной, то решение уравнения (10.15) имеет вид:

где ω = круговая частота затухающих колебаний. График таких колебаний представлен на рис. 10.3.

Рис. 10.3. График зависимости смещения от времени при затухающих колебаниях (φ₀ -. 0)

В этом случае колебательный характер движения сохраняется, но амплитуда колебаний уменьшается со временем по экспоненциальному закону А = Α₀·ехр(— β · t). Круговая частота колебаний становится меньше, чем при отсутствии силы трения. Период затухающих колебаний в этом случае возрастает и определяется формулой, показывающей зависимость от коэффициента трения:

Быстрота убывания амплитуды колебаний зависит от коэффициента затухания: чем больше р, тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда.

Количественно степень затухания характеризуется безразмерной величиной — логарифмическим декрементом затухания λ:

б) ω₀²< β² (сильное затухание), то колебательное движение не возникает. Период колебаний становится мнимой величиной. В этом случае запас механической энергии тела к моменту его возвращения в положение равновесия полностью или почти полностью расходуется на преодоление сил трения и тело останавливается. Такое движение называется апериодическим.

Не нашли, что искали? Воспользуйтесь поиском: