
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Абсолютная величина и направление вектора
Векторы.
Вектором мы будет называть направленный отрезок.
Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться срочными латинскими буквами a, b, c, …. Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова ‘‘вектор’’ над буквенным обозначением вектора иногда ставится стрелка или черта.
Векторы  и
и  называются одинаково направленными, если полупрямые AB и CD одинаково направлены. Векторы
называются одинаково направленными, если полупрямые AB и CD одинаково направлены. Векторы  и
и  называются противоположно направленными, если полупрямые AB и CD противоположно направлены. Векторы
называются противоположно направленными, если полупрямые AB и CD противоположно направлены. Векторы  и
и  одинаково направлены, а векторы
одинаково направлены, а векторы  и
и  противоположно направлены.
противоположно направлены.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора 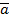 обозначается
обозначается  .
.
Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается  . О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.
. О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.
Равенство векторов
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает,что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине.
Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
Действительно, пусть  и
и  одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку C в точку A,совмещает полупрямую CD с полупрямой AB, так как они одинаково направлены.
одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку C в точку A,совмещает полупрямую CD с полупрямой AB, так как они одинаково направлены.
А так как отрезки AB и CD равны, то при этом точка D совмещается с точкой B, т. е. параллельный перенос переводит вектор  в вектор
в вектор  . Значит, векторы
. Значит, векторы  и
и  равны,что и требовалось доказать.
равны,что и требовалось доказать.
Координаты вектора
Пусть вектор 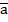 имеет началом точку
имеет началом точку  ,а концов ─ точку
,а концов ─ точку  . Координатами вектора
. Координатами вектора 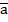 будем зазывать числа
будем зазывать числа  ,
, 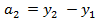 .
.
Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае 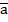 (
( ) или просто (
) или просто ( Координаты нулевого вектора равны нулю.
Координаты нулевого вектора равны нулю.
Из формулы выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами  равна
равна 
Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.
Действительно, пусть  , и
, и  начало и конец вектора
начало и конец вектора 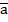 .Так как равный ему вектор
.Так как равный ему вектор  получает их вектора
получает их вектора 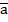 параллельным переносом, то его началом и концом будут соответственно
параллельным переносом, то его началом и концом будут соответственно  ,
, 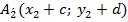 .
.
Отсюда видно, что оба вектора 
 имеют одни и те же координаты:
имеют одни и те же координаты:  .
.
Сложение векторов.
Суммой вектором 
 с координатами
с координатами  и
и  называется вектор
называется вектор  с координатами
с координатами  ,
,  т. е.
т. е.

Для любых векторов  ,
,  ,
, 
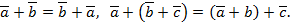
Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равным координатам равны.
Теорема. Каковы бы ни были точки A, B, C, имеет место векторное равенство
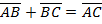
Доказательство. Пусть 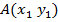

 данные точки. Вектор
данные точки. Вектор 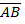 имеет координаты
имеет координаты  ,вектор
,вектор 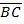 имеет координаты
имеет координаты  .Следовательно, вектор
.Следовательно, вектор  имеет координаты
имеет координаты  .А это есть координаты вектора
.А это есть координаты вектора  .
.
Значит, векторы  и
и  равны. Теорема доказана.
равны. Теорема доказана.
Теорема дает следующий способ построения суммы произвольных векторов 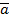 и
и  . Надо от конца вектора
. Надо от конца вектора 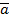 отложить вектор
отложить вектор  , равны вектору
, равны вектору  . Тогда вектор, начало которого совпадает с началом вектора
. Тогда вектор, начало которого совпадает с началом вектора  , а конец ─ с концом вектора
, а конец ─ с концом вектора  , будет суммой векторов
, будет суммой векторов 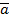 и
и  . Такой способ получения суммы двух векторов называется <<правилом треугольника >> сложения векторов.
. Такой способ получения суммы двух векторов называется <<правилом треугольника >> сложения векторов.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах (<<правило параллелограмма >>).
Действительно 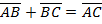 , а
, а 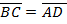 . Значит
. Значит  .
.
Разностью векторов  и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  :
:  . Отсюда находим координаты вектора
. Отсюда находим координаты вектора  :
:
 .
.
5.Умножение вектора на число
Произведем вектора 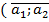 ) на число
) на число  называется вектором
называется вектором  ), т. е.
), т. е. 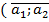 )
)  ).
).
Из определения операции умножения вектора на число следует, что для любого вектора  и чисел
и чисел  ,
, 

Для любых двух векторов 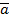 и
и  и числа
и числа 

Теорема. Абсолютна величина вектора  равна
равна  . Направление вектора
. Направление вектора  при
при 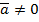 совпадает с направлением вектора
совпадает с направлением вектора  ,если
,если  и противоположно направлению вектора
и противоположно направлению вектора  , если
, если  .
.
Абсолютная величина вектора  равна:
равна:

Не нашли, что искали? Воспользуйтесь поиском: