Скалярное произведение векторов. Скалярным произведение векторов и называется число

Скалярным произведение векторов и называется число

Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение 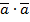обозначается и называется скалярным квадратом. Очевидно .

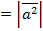Из определения скалярного квадрата произведения векторов следует, что для любых векторов , ,

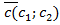
= a +

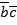
Действительно, левая часть равенства есть 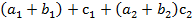, а правая . Очевидно, они равны.

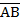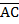Угол между ненулевыми векторами и называется угол BAC. Угол между любыми двумя ненулевыми векторами называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.

Теорема. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

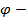Доказательство. Пусть данные векторы и угол между ними. Имеем:

=

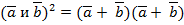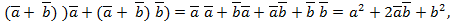
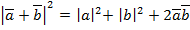
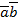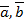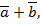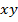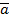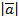Отсюда видно, что скалярноепроизведение выражается через длины векторов и а поэтому не зависит от выбора систем координат, т. е. скалярное произведение не изменится, если систем координат выбрать специальным образом. Возьмем систему координат .При таком выборе системы координат координатами вектора будут и 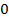, а координатами вектора 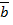будут и 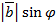.Скалярное произведение

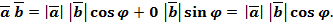
Теорема доказана. Из теоремы следует, что если векторы перпендикулярны, то их скалярная произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.

Не нашли, что искали? Воспользуйтесь поиском: