ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Разложение вектора по координатным осям
Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называют координатными векторами или ортами. Мы будем их обозначать 
(1;0) на оси 
и 
(0;1) на оси 
.
Так как координатные векторы отличны от нуля и не коллинеарные, то любой вектор 
допускает разложение по этим векторам:
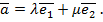
Найдем коэффициенты 
и 
этого разложения. Умножим обе части равенства 
на вектор 
.
Так как:
Аналогично, умножая обе части равенства на вектор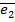 
,получаем 
Таки образом, для любого вектора 
получается разложение:
.
Не нашли, что искали? Воспользуйтесь поиском: