Достаточное условие экстремума).

Билет № 1

1. Матрицы. Виды матриц.

2. Условия постоянства и монотонности функции.

3. Задачи 3, 4, 5 из приложения к билету.

1)Определение матрицы. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.

Квадратной матрицей n-го порядка называется матрица размера n×n.

Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

Нулевой называется матрица, все элементы которой равны нулю.

2) Пусть функция имеет производную в каждой точке интервала . Для того, чтобы этафункция была постоянной на интервале , необходимо и достаточно выполнение условия для .

Билет № 2

1. Действия над матрицами.

2. Числовая последовательность и её предел.

3. Задачи 3, 4, 5 из приложения к билету.

1) Суммой двух матриц одинаковой размерности AVLB называетсяматрица С такой же размерности, получаемая из этих матриц сложением соответствующих элементов

С = А+В.

Разность матриц есть действие обратное сложению, т.е. чтобы найти разность двух матриц одинаковой размерности, следует произвести вычитание соответствующих элементов

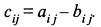
Умножение матрицы на матрицу. Под произведением матрицы А размерности на матрицу В размерности понимается матрица С размерности 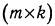, получаемая перемножением элементов матрицы А на элементы матрицы В по

правилу т. е. по правилу «строки на столбец».

n=n 2* 2 = 2 *3

2) Числовой последовательностью называется бесконечное множество чисел

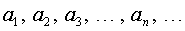следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого 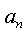задается как функция целочисленного аргумента, т.е. .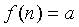

Число А называется пределом последовательности, если для любого 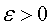существует число 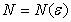, такое, что при выполняется неравенство . Если число А есть предел последовательности, то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Билет № 3

1. Определители 2-го и 3-го порядков. Основные свойства.

2. Взаимное расположение прямой и плоскости.

3. Задачи 3, 4, 5 из приложения к билету.

1) Определителем 2-го порядка называется число, обозначаемое выражением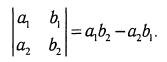

Определителем 3-го порядка называется число, обозначаемое выражением

Определителем п-го порядка называется число

2) взаимное расположение прямой и плоскости ,

Билет № 4

1. Канонические уравнения прямой в пространстве.

2. Замена переменной в неопределённом интеграле.

3. Задачи 3, 4, 5 из приложения к билету.

1) Уравнение прямой в каноническом виде

направляющий вектор прямой 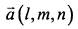; 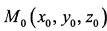-точка ч/з которую проходит прямая

2) метод интегрирования- метод подстановки(замены переменной) x=φ(t) dx= φ’(t)dt- это формула замены переменной в неопределенном интеграле

Билет № 5

1. Уравнение плоскости «в отрезках на осях».

2. Таблица основных производных.

3. Задачи 3, 4, 5 из приложения к билету.

1) уравнение плоскости в отрезках на осях 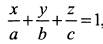где отрезки, которые отсекает плоскость на координатных осях

2) таблица основных производных:

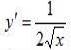
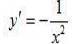
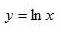
Билет № 6

1. Общее уравнение плоскости в пространстве.

2. Вычисление пределов по правилу Лопиталя.

3. Задачи 3, 4, 5 из приложения к билету.

1) Общее уравнение плоскости. Всякая плоскость определяется уравнением первой степени с тремя неизвестными 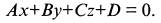А, В, С не равны 0

2) Если при функции 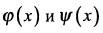одновременно стремятся к нулю или 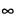, то предел их отношения равен пределу отношения их производных, т. е. При этом предполагается, что 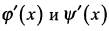существуют и конечны.

Если же отношение производных также будет представлять случай или , можно снова и снова применять правило Лопиталя.

Билет № 7

1. Парабола.

2. Определённый интеграл, его основные свойства.

3. Задачи 3, 4, 5 из приложения к билету.

1) Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой ее фокусом и от данной прямой, называемой ее директрисой. Каноническое уравнение параболы имеет вид 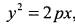где р— параметр параболы, равный расстоянию от фокуса до директрисы.

эксцентриситет любой параболы равен единице

Общее уравнение параболы, ось симметрии которой параллельна оси ординат, имеет вид

2) Определенным интегралом от функции f(x) на отрезке [а,b] называется число, равное общему пределу всех интегральных сумм при стремлении к нулю максимального отрезка разбиения Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, отрезок [а,Ь] —промежутком интегрирования.

Свойства: 1. Определенный интеграл зависит только от вида функции /(х) и пределов интегрирования, но не зависит от обозначения переменной интегрирования, т. е.

2. Определенный интеграл меняет знак при перестановке пределов интегрирования

3. Интеграл с одинаковыми пределами интегрирования равен нулю

4. Постоянный множитель можно выносить за знак интеграла

5. Интеграл от суммы функций равен сумме интегралов от этих функций

6. Отрезок интегрирования можно разбивать на части

Билет № 8

1. Гипербола.

2. Необходимое и достаточное условия экстремума функции.

3. Задачи 3, 4, 5 из приложения к билету.

1) Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная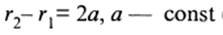

Каноническое уравнение гиперболы имеет вид

где а —действительная полуось; b — мнимая полуось гиперболы.

Эксцентриситетом гиперболы называется отношение фокусного расстояния гиперболы с к ее действительной оси, то есть

Уравнения директрис

Если полуоси гиперболы равны, то гипербола называется равносторонней и ее уравнение имеет вид Уравнение равносторонней гиперболы, отнесенной к своим

асимптотам, как к осям координат, имеет вид

2) Необходимое условие экстремума). Если функция y =f(x) в точке х₀ имеет экстремум, то производная f^/(x ₀ ) равна нулю.

Точка, в которой производная равна нулю, называется стационарной.

Стационарная точка необязательно является точкой экстремума функции.

Точка в которой производная функции равна 0 или не существует, называется критической точкой.

Достаточное условие экстремума).

Пусть функция f(x) непрерывна на отрезке [a, b], а точка x₀ из этого отрезка является критической. Тогда:

1) если f^/(x) < 0 на (a;x₀) и f^/(x) > 0 на (x₀;b), то точка x₀–точка минимума функции f(x);

2) если f^/(x) > 0 на (a;x₀) и f^/(x) < 0 на (x₀;b), то точка x₀–точка максимума функции f(x).

Билет № 9

1. Эллипс.

2. Основная формула интегрального исчисления (Ньютона – Лейбница).

3. Задачи 3, 4, 5 из приложения к билету.

1) Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек плоскости, называемых фокусами эллипса, есть величина постоянная

Каноническое уравнение эллипса имеет вид где — большая и малая полуоси эллипса.

Эксцентриситетом эллипса называется отношение фокусного расстояния эллипса с к его большой оси

Директрисами эллипса называются прямые параллельные его малой оси и отстоящие от нее на расстоянии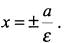

Отношение расстояния любой точки эллипса до фокуса к расстоянию ее до соответствующей этому фокусу директрисы есть величина постоянная, равная эксцентриситету эллипса

Фокальные радиусы некоторой точки М могут быть найдены по формулам

2) Пусть функция y=f(x) интегрируема на [a;b], тогда она интегрируема на всех [a;x], где x принадлежит [a;b]. 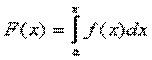- определенный интеграл с переменным верхним пределом x.

Если функция f(x) интегрируема на [a;b], то имеет место формула:

- где F(x) - первообразная.

Билет № 10

1. Окружность на плоскости.

2. Интегрирование «по частям» в неопределённом интеграле.

3. Задачи 3, 4, 5 из приложения к билету.

1) Окружностью называют геометрическое место точек, равноудаленных от одной точки, называемой центром окружности. Уравнение окружности имеет вид

Где 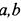— координаты центра окружности — радиус окружности.

2) Формула интегрирования по частям

Для применения формулы интегрирования по частям подынтегральное выражение следует представить в виде произведения двух множителей За выбирается функция, которая

при дифференцировании упрощается, а за выбирается такое выражение, содержащее 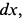из которого посредством интегрирования можно найти

Билет № 11

1. Каноническое уравнение прямой на плоскости.

2. Таблица основных неопределённых интегралов.

3. Задачи 3, 4, 5 из приложения к билету.

1) 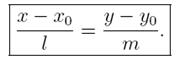здесь =(m, n)-вектор, параллельный прямой. Он называется направляющим вектором прямой

2)

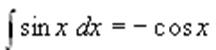
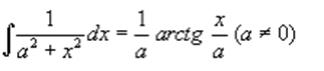
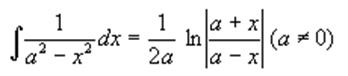
Билет № 12

1. Общее уравнение прямой на плоскости.

2. Предел функции в точке и на бесконечности. Свойства пределов.

3. Задачи 3, 4, 5 из приложения к билету.

1) Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А² + В² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

2) Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Не нашли, что искали? Воспользуйтесь поиском: