Основные правила нахождения производной

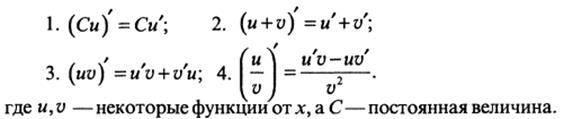
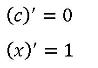
Билет № 17

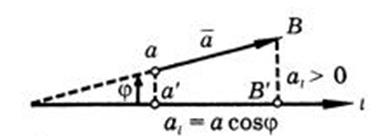
1. Проекция вектора на ось.

2. Наибольшее и наименьшее значения функции на отрезке.

3. Задачи 3, 4, 5 из приложения к билету.

1) Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора

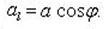
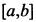2) Наибольшим значением функции а некотором отрезке называется самое большое, а наименьшим значением — самое меньшее из всех ее значений.

Если функция непрерывна в некотором интервале и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале (конечном или бесконечном).

Билет № 18

1. Базис и координаты вектора в пространстве.

2. Производная функции, заданной параметрически.

3. Задачи 3, 4, 5 из приложения к билету.

1) Базисом в пространстве называются три некомпланарных вектора 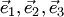, взятые в определённом порядке. Эти векторы 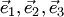называются базисными.

Коэффициенты 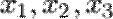в разложении называются координатами вектора 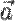относительно базиса 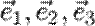(число 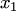, называют абсциссой, 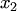— ординатой, а 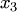— аппликатой вектора).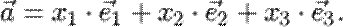

2) Если функциональная зависимость между переменными 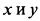задана параметрически. 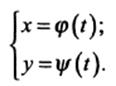TO производная от 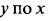равна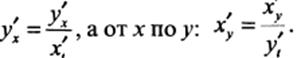

Билет № 19

1. Базис и координаты вектора на плоскости.

2. Сравнение и эквивалентность бесконечно малых.

3. Задачи 3, 4, 5 из приложения к билету.

1) Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определённом порядке. Эти векторы называются базисными.

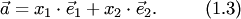
Коэффициенты 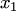и 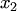в разложении (1.3) называются координатами вектора а относительно базиса (число 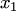называют абсциссой, а 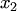— ординатой вектора ).

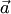2) Ф-ция 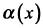назыв бесконечно малой при 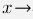x0, если lim 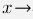x0 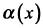=0 Отношение бесконечно малых величин образует так называемую неопределённость .

Если 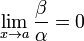, то β — бесконечно малая высшего порядка малости, чем α.

Если 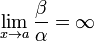, то β — бесконечно малая низшего порядка малости, чем α.

Если 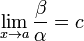(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.

Если 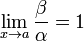, то бесконечно малые величины α и β называются эквивалентными ().

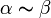При 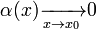справедливы следующие соотношения эквивалентности

·

·

·

·

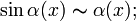
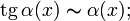
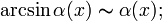
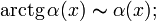
Билет № 20

1. Векторы. Линейные действия над векторами.

2. Непрерывность функции в точке. Точки разрыва.

3. Задачи 3, 4, 5 из приложения к билету.

1) Вектором 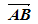называется направленный отрезок с началом в точке A и концом в точке B.

Суммой векторов 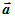и 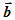называется вектор 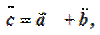который получается при совмещении конца вектора 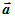с началом вектора 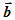. Тогда началом вектора 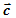будет начало вектора 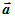, а концом вектора 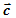- конец вектора .

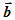Сумма векторов обладает свойствами сочетательности и переместительности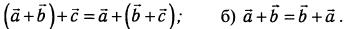

Вектор 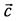называется разностью векторов 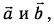если сумма векторов 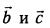равна вектору 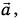т. е. если

2) Функция 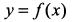непрерывна в точке х = а, если пределы слева и справа равны и равны значению функции в этой точке, т. е.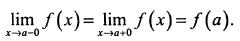

Функция 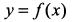непрерывна в точке х = а, если она определена в этой точке и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, 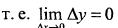вблизи точки а.

Сумма, разность и произведение конечного числа непрерывных функций есть функция непрерывная.

Непрерывная на отрезке 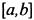функция принимает любое промежуточное значение между ее наименьшим т и наибольшим М значением, то есть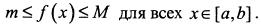

Значения аргумента, которые не удовлетворяют условиям непрерывности, называются точками разрыва функции. При этом различают два рода точек разрыва функции.

Если при 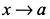слева функция имеет конечный предел 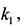а при 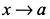справа функция имеет конечный предел 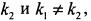то говорят, что функция при 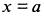имеет разрыв первого рода.

Если значение функции при 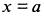равно 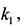то говорят, что функция непрерывна слева; если же 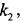то говорят, что функция непрерывна справа.

Если 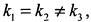говорят, что функция имеет в точке а устранимый разрыв.

Если при 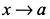справа или слева, предел функции не существует или равен бесконечности, то есть 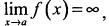то говорят, что при 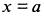функция имеет разрыв второго рода.

Билет № 21

1. Миноры и алгебраические дополнения. Теорема разложения.

2. Бесконечно малые и бесконечно большие функции, связь между ними.

3. Задачи 3, 4, 5 из приложения к билету.

1) Минором некоторого элемента определителя называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых этот элемент находится. Так для элемента 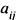минор обозначается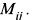

Алгебраическим дополнением некоторого элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых находится этот элемент—число четное и со знаком минус, если эта сумма — число нечетное. Алгебраическое дополнение элемента 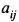будет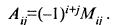

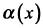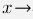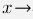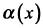2) Ф-ция назыв бесконечно малой при x0, если lim x0 =0

Ф-ция 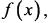называется бесконечно большой при 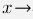x0, если lim 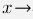x0 =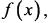

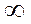
(1/0)= 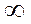обратная к бесконечно малой при 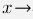x0, бесконечно большая и наоборот (1/ 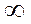)=0

Билет № 22

1. Обратная матрица и её вычисление.

2. Понятие функции. Классы функций. Сложная функция.

3. Задачи 3, 4, 5 из приложения к билету.

1) Обратной матрицей по отношению к заданной квадратной матрице А называется такая квадратная матрица, обозначаемая 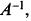которая удовлетворяет равенствам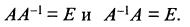

Нахождение обратной матрицы :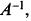

1) находим определитель |А| = 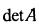Если он не равен нулю, то

2) находим алгебраические дополнения 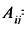всех элементов матрицы А

3) составляем из них матрицу А*

4) транспорируем ее (А*)^Т

5) получаем обратную матрицу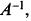

2) Переменную х называют независимой переменной или аргументом, а у — функцией. Функция может задаваться аналитически, графически и таблично.

К основным элементарным функциям относятся пять классов функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.

Пусть каждому значению переменной х ставится в соответствие определенное значение переменной 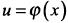а каждому уже определенному значению и ставится в соответствие определенное значение 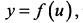тогда соответствие между значениями имеет вид 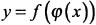и определяет у как сложную функцию от х, т. е. функцию от функции.

Утверждено на заседании кафедры «16 09 2011 г., протокол № 2. Заведующий кафедрой ____________________________М.Е.Исин

_______________________________________________________________________________________________________________________________

Павлодарский государственный университет имени С.Торайгырова

Кафедра математики

Экзаменационный билет по дисциплине «Математика I»

Составитель доц. Тихомиров Ю.В.

Билет № 23

1. Системы линейных алгебраических уравнений.

2. Взаимное расположение прямых в пространстве.

3. Задачи 3, 4, 5 из приложения к билету.

1) Система 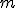линейных алгебраических уравнений с 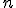неизвестными — это система уравнений вида 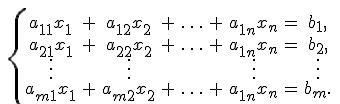Матрица коэффициентов системы; столбец неизвестных Х(х1 х2 х_n); В(b1 b2 b_n) столбец свободных членов

2) Взаимное расположение прямых

y=k₁x+b₁ y= k₂x+b₂

k1=k2-параллельны, k1k2=-1-перпендикулярны

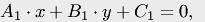
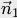={А₁, В₁} 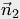={А₂, В₂}

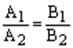-параллельны прямые (прямые не совпадают и не пересекаются)

Необходимым и достаточным условием перпендикулярности прямых

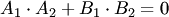
Утверждено на заседании кафедры «16 09 2011 г., протокол № 2. Заведующий кафедрой ____________________________М.Е.Исин

_______________________________________________________________________________________________________________________________

Павлодарский государственный университет имени С.Торайгырова

Кафедра математики

Экзаменационный билет по дисциплине «Математика I»

Составитель доц. Тихомиров Ю.В.

Билет № 24

1. Матричный метод решения систем линейных алгебраических уравнений.

2. Касательная и нормаль к плоской кривой.

3. Задачи 3, 4, 5 из приложения к билету.

1) Пусть дана система линейных уравнений

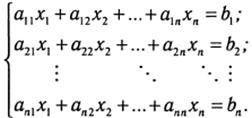
Если ввести матричные обозначения

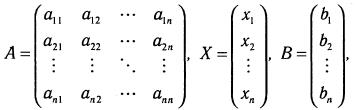
то систему можно записать матричным уравнением 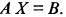Решение системы матричным методом определяется соотношением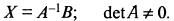

2)Из геометрического смысла производной следует, что угловой коэффициент касательной к кривой 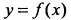в точке 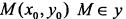равен значению производной в этой точке, т. е. 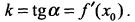касательной к кривой в точке имеет вид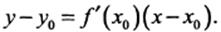

Нормалью к кривой в точке 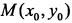называется прямая, проходящая через точку М перпендикулярно касательной к кривой в этой точке. В силу условия перпендикулярности двух прямых 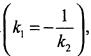уравнение нормали имеет вид

Утверждено на заседании кафедры «16 09 2011 г., протокол № 2. Заведующий кафедрой ____________________________М.Е.Исин

Павлодарский государственный университет имени С.Торайгырова

Кафедра математики

Экзаменационный билет по дисциплине «Математика I»

Составитель доц. Тихомиров Ю.В.

Билет № 25

1. Метод Крамера решения систем линейных алгебраических уравнений.

2. Вычисление площадей при помощи определённого интеграла.

3. Задачи 3, 4, 5 из приложения к билету.

1) Решение системы двух линейных уравнений с двумя неизвестными

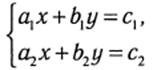по формулам Крамера имеет вид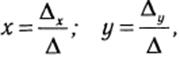

Где основной и дополнительные определители системы.

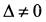— система совместна, имеет единственное решение;

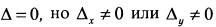— система несовместна, не имеет решения;

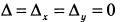— система неопределенна, т. е. имеет бесчисленное множество решений (система сводится к одному уравнению).

Однородная система трех линейных уравнений с тремя неизвестными

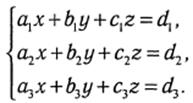
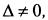система имеет единственное решение, определяемое по формулам Крамера решению

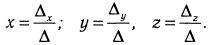
2) Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a; b ] функции f (x), осью Ох и прямыми х=а и х= b:

.

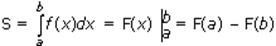Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a; b ] функции f (x), осью Ох и прямыми х=а и х= b: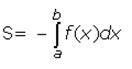

Площадь фигуры, ограниченной графиками непрерывных функций f (x), 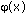и прямыми х=а, х= b:

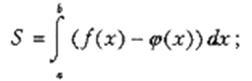
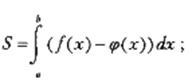
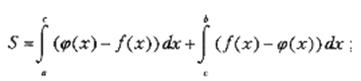
Площадь фигуры, ограниченной графиками непрерывных функций f (x), 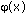и осью Ох: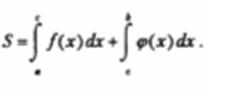

Не нашли, что искали? Воспользуйтесь поиском: