Обозначение предела функции

Предел функции обозначается как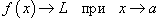

или через символ предела функции: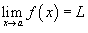

Свойства пределов функции:

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела: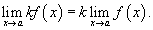

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

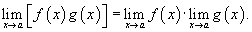
Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

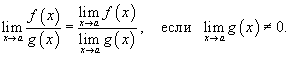
Билет № 13

1. Уравнение прямой с угловым коэффициентом.

2. Первообразная и неопределённый интеграл, их основные свойства.

3. Задачи 3, 4, 5 из приложения к билету.

1) 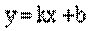называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

2) Функция называется первообразной от функции на отрезке если во всех точках этого отрезка выполняется равенство

Если функция является первообразной для 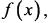то выражение 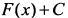называется неопределенным интегралом от функции 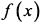и обозначается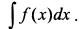

Таким образом, по определению 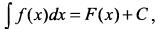если

Билет № 14

1. Смешанное произведение векторов, его свойства.

2. Производная функции в точке, её геометрический и механический смысл.

3. Задачи 3, 4, 5 из приложения к билету.

1) Смешаным произведнием трех векторов называется выражение вида Если векторы заданы своими координатами, то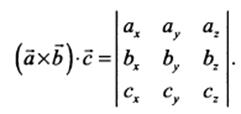

2) Производной от функции в точке называется предел отношения приращения функции к приращению аргумента Если этот предел конечный, то функция называется дифференцируемой в точке

Геометрический смыл

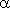- угол наклона секущей

Механический смысл

v (t₀) = x’ (t₀), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по

времени: a = v’ (t).

Билет № 15

1. Векторное произведение векторов, его свойства.

2. Первый и второй замечательные пределы.

3. Задачи 3, 4, 5 из приложения к билету.

1)Векторное произведение векторов назыв вектор, обозначаемой ([ 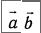],[ ]) и удовлетворяющий трем св-вам:

1) длина векторного произведения равна-

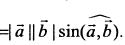
2) вектор перпендикулярен векторам

3) вектор направлен в ту сторону с которой поворот от 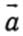к 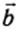видится против часовой стрелки.

Св-ва геометрические

1) длина векторного произведения численно равна площади параллелограмма, построенного на векторах

2) векторы коллинеарны тогда и только тогда, когда 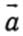* 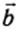=0. В частности 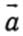* 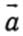=0

Алгебраические:

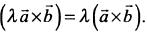
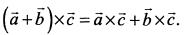
2. Замечательные пределы 1. Первый замечательный предел

2. Второй замечательный предел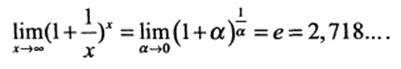

Билет № 16

1. Скалярное произведение векторов, его свойства.

2. Основные правила нахождения производных. Примеры.

3. Задачи 3, 4, 5 из приложения к билету.

1) Скалярным произведением двух векторов называется скаляр (число), равное произведению модулей перемножамых векторов на косинус угла между ними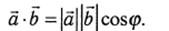

Свойства

1. Переместительность
2. Распределительность

3.Скалярный множитель можно выносить за знак скалярного произведения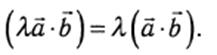

4. Скалярный квадрат вектора равен квадрату его модуля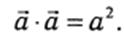

5. Скалярное произведение единичных векторов определяется формулами

Не нашли, что искали? Воспользуйтесь поиском: