
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Формула Бине и некоторые ее применения
Напомним (см. 11.3, формула (5)), что производящая функция для последовательности чисел Фибоначчи имеет вид
F (z) = F 0 + F 1 z + F 2 z 2 + … =
z.
 1 − z − z 2
1 − z − z 2
Корнями характеристического многочлена
k (z) = z 2 – z –1
являются числа

 б 1 5
б 1 5

 и в 1− 5.
и в 1− 5.
Число Фибоначчи как функция своего номера
представляется в виде:
или
Fn =
б n − в n
 5
5
, (4)
n
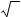 1 5
1 5
n
 1− 5
1− 5

 −
−
2 2
Fn
,
 5
5
Формула (4) называется формулой Бине.
Так как 2 = + 1, то любую степень числа можно представить в виде целочисленной комбинации a + b. Оказывается, коэффициентами служат числа Фибоначчи:
k +2 = Fk +2 + Fk +1.
Формула Бине позволяет убедиться в этом прямой проверкой.
Приведем несколько оценок чисел Фибоначчи.
|
 Число Фибоначчи Fn есть ближайшее целое к чи слу.
Число Фибоначчи Fn есть ближайшее целое к чи слу.
|
Следовательно,


|
б n − в n б n
 −
−
 5 5
5 5


|
5 2
Из (4) вытекает также следующее свойство.
 С ростом n числа Фибоначчи неограниченно сближаются с
С ростом n числа Фибоначчи неограниченно сближаются с
 членами геометрической прогрессии с начальным членом 1 и
членами геометрической прогрессии с начальным членом 1 и
знаменателем
5 1:
 2
2
n
lim F − б
0.

|
|
Отношение соседних чисел Фибоначчи (следующего к
|
Действительно,
2 ≈ 0,618.

 5 1
5 1

 Fn
Fn
б n − в n
1− (в / б).
Fn 1
б n 1 −в n 1
б − в(в / б) n
Так как / < 1, то (/) n с ростом n стремится к нулю.
Следовательно,

 lim
lim
Fn 1
≈ 0,618.
n →∞ Fn 1 б
Из предыдущего равенства следует, что

 lim
lim
Fn 1
≈ 0,382.
n →∞ Fn 2 б 2
Установим справедливость формулы, которая дает представление чисел Фибоначчи в виде суммы биномиальных коэффициентов, и как ее следствие получим одно тождество для биномиальных коэффициентов.
При любом n справедливо следующее равенство:
Fn 1
∑ C k − k. (6)
|
Заметим сначала, что при четном n равенство (6) имеет вид
0 1 n / 2
а при нечетном –
Fn 1 Cn
Cn −1 ... Cn / 2,
0 1 (n −1) / 2
Например:
Fn 1 Cn
Cn −1 ... C (n 1) / 2.
0 1 2
0 1 2
F 5 C 4
C 3 C 2;
F 6 C 5
C 4 C 3.
Для доказательства (6) воспользуемся производящей функцией последовательности чисел Фибоначчи:
z
F (z) = F 0 + F 1 z + F 2 z 2 +… =
 1− z − z 2
1− z − z 2
. (7)
Используя формулу для суммы членов бесконечно убывающей геометрической прогрессии, преобразуем правую часть равенства (7):
z
 1− z − z 2
1− z − z 2
z ⋅
 1− (z z 2)
1− (z z 2)
= z (1 + (z + z 2) + (z + z 2)2 +…) =
|
низких, чем n + 1. Так как
|
z p 1 ∑ C k z k k ≤ p
∑ C k zk p 1,
k ≤ p
то коэффициент при zn +1 получается суммированием по p всех
|
C k, что k + p +1 = n + 1 и k ≤ p.
Последние условия означают, что p = n – k и 2 k ≤ n. Таким
|
C k k, 2 k ≤ n, и
получаем сумму, стоящую в правой части (6), что и доказывает это равенство.
С учетом формулы Бине равенство (7) может быть записано
следующим образом:
1 1
n 1
 5
5
1 −
n 1
 5
5
|
|


|
|
|
− .
|
Золотое сечение
Разделим отрезок AB на части так, чтобы большая часть была бы средним пропорциональным между всем отрезком и
меньшей его частью. Иными словами, мы ищем точку C такую,
что AC: BC = BC: AB (рис. 1).
 A C D B
A C D B
Рис. 1
Пусть BC = x ⋅ AB. Тогда AC = x ⋅ BC = x 2⋅ AB. Так как
AC + BC = AB, то
 x 2 + x = 1. (9)
x 2 + x = 1. (9)
Уравнение (9) имеет два решения:

 − 1
− 1
5 ≈ 0,618
и −1−
 2
2
5 ≈ −1,618.
Точка C соответствует положительному решению

 x −1 5.
x −1 5.
Разбиение отрезка AB на две части точкой C называют
золотым сечением этого отрезка.
Точно так же можно получить золотое сечение отрезка AB
точкой D такой, что BD: AD = AD: AB.
Оказывается, точка D дает золотое сечение отрезка BC.
Действительно:
BC = x ⋅ AB, AD = x ⋅ AB, BD = (1 – x)⋅ AB,
и, значит, CD = BC – BD = (2 x – 1)⋅ AB. Таким образом,



 CD 2 x −1;
CD 2 x −1;
BD 1− x.
BD 1 − x BC x
 Так как x служит корнем уравнения x 2 + x – 1 = 0, то, как
Так как x служит корнем уравнения x 2 + x – 1 = 0, то, как
легко проверить,
2 x −1 1− x. Следовательно,
 1 − x
1 − x
 −1 5
−1 5
x
 CD
CD
BD
 BD.
BD.
BC
Заметим, что x 2
– это предел, к которому стремится
отношение соседних чисел Фибоначчи Fn / Fn +1. Приближение золотого сечения, изображенного на рис. 1, можно получить,
взяв точки C ′ и D ′ такие, что
 AC ′ 1−
AC ′ 1−
F
|
Fn 2
Fn
 Fn 2
Fn 2
AB;
AD ′ F n 1
 Fn 2
Fn 2
 AB.
AB.
К «золотому» пределу
−1 5
1, где
б
б 1 5
, отношение
un / un +1 стремится для любой последовательности с положительными членами, удовлетворяющей рекуррентному соотношению un +2 = un +1 + un. В самом деле, члены любой такой последовательности имеют вид
 un = a n + b n,
un = a n + b n,
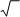 где
где
б 1 5
и в
1− 5
– корни характеристического уравнения
x 2 – x – 1 = 0. Поскольку все члены последовательности (un)
положительны, a ≠ 0. Так как || 1, то () n →0 при n →∝.
Следовательно,
б n в n
1 b в n

 un a b
un a b


 a б
a б

un 1
a б n 1 b в n 1
б b в n в б
a б
Таким образом, аппроксимировать золотое сечение можно с помощью любой положительной последовательности (un), члены которой удовлетворяют рекуррентному соотношению un +2 = un +1 + un.
Золотое сечение используется в техническом анализе при
торговли ценными бумагами на инвестиционных рынках.
Центральную роль в так называемом анализе Фибоначчи играют Фиб-узлы (или уровни Ди Наполи). На ценовой волне берутся две крайние точки A и B и отрезок AB делится точками C и D (рис. 2) подобно тому, как это сделано на рис. 1. Полученные точки называются Фиб-узлами. Считается, что в этих точках происходит значительное сопротивление изменению цен при обратном движении.


 B
B





 D (F 3) 0.618
D (F 3) 0.618




 C (F 5)
C (F 5)
0.382


 A
A
Рис. 2
В качестве Фиб-узлов используются также близкие к ним точки – F 3 и F 5 – Фиб-узлы, расположенные на уровнях 3/8 и 5/8:
F 3
A F 4 B − A ;
 F 6
F 6
F 5
A F 5 B − A .
 F 6
F 6
Некоторое теоретическое объяснение эмпирически обоснованному выбору Фиб-узлов дается в следующем параграфе.
Не нашли, что искали? Воспользуйтесь поиском: