Числа Каталана. Случайное блуждание

В этом параграфе мы исследуем рекуррентное соотношение, которое встречается во многих задачах (см., например, далее подсчет числа бинарных деревьев), в том числе в задачах финансового анализа.

Рассмотрим биномиальную решетку цен актива. Пусть, как и ранее, u > 1 – повышающий коэффициент, а d < 1 – понижающий. Если стоимость актива повышалась p раз и понижалась q раз, то она станет равной S 0 updq.

Сопоставим каждому пути на решетке, последовательность

вида

(a 1, a 2, …, am), (16) состоящую из –1 и 1, в которой –1 соответствует понижению стоимости, а 1 – повышению. Пусть a = a 1 + a 2 +…+ am. Число a показывает на сколько число повышений больше числа понижений. Число «минус единиц» q в последовательности (16) равно (n – a)/2, число «единиц» p равно (n + a)/2. Стоимость актива с последовательностью повышений-понижений (16) к моменту m равна

S 0 updq = S 0 u (n + a)/2 d (n – a)/2.

Предположим, что p + q = 2 n – четное число. Наибольшее

ведет в узел S

0 undn. На этих путях число

понижений равно числу повышений. Если считать, что ud = 1, то стоимость актива в результате развития событий по пути, приводящему в узел S 0 undn, остается неизменной: S 0 undn = S 0. Мы займемся подсчетом числа путей, на которых стоимость актива ни разу не опускается ниже S 0. Иными словами, нас интересует число последовательностей

(a 1, a 2, …, a 2 n), (17)

для которых сумма всех элементов равна нулю:

a 1 + a 2 +…+ a 2 n = 0,

а все частичные суммы неотрицательны:

s 1 = a 1 ≥ 0, s 2 = a 1 + a 2 ≥ 0, …,

s 2 n –1 = a 1 + a 2 +…+ a 2 n –1 ≥ 0.

Про такие последовательности будем говорить, что они сбалансированы. Графически последовательность вида (17) может быть представлена диаграммой частичных сумм. На рис. 2 представлены две сбалансированные последовательности длины 4 (при n = 2); на рис. 3 – пять сбалансированных последовательностей длины 6 (при n = 3). Сбалансированность означает, что диаграмма не опускается ниже нулевого уровня.

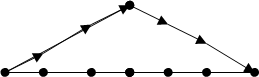
Рис. 2

Рис. 3

Обозначим через Cn – число различных сбалансированных последовательностей длины 2 n. Ясно, что C 0 = 1 (имеется ровно одна пустая последовательность) и С 1 = 1. Мы видели также, что С 2 = 2 и С 3 = 5.

При n > 0 всякая сбалансированная последовательность начинается с единицы и заканчивается минус единицей:

a 1 = 1, a 2 n = –1.

Если все частичные суммы сбалансированной последовательности (17) положительны, то последовательность (a 2, …, a 2 n –1), имеющая длину 2 n – 2, также оказывается сбалансированной. Обратно, любую сбалансированную последовательность длины 2 n – 2 можно дополнить до сбалансированной последовательности длины 2 n, приписав к ней слева единицу, а справа – минус единицу. Тем самым между множеством сбалансированных последовательностей длины 2 n с положительными частичными суммами и множеством всех сбалансированных последовательностей длины 2 n – 2 устанавливается взаимно однозначное соответствие. Следовательно, число сбалансированных последовательностей длины 2 n с положительными частичными суммами равно Cn –1 – общему числу сбалансированных последовательностей длины 2 n – 2.

Рассмотрим теперь произвольную сбалансированную последовательность (17), имеющую нулевые частичные суммы. Пусть 2 k < 2 n – номер последней частичной суммы, равной нулю. Последовательность (17) можно разбить на две сбалансированные последовательности

(a 1, a 2, …, a 2 k), (a 2 k +1, a 2, …, a 2 n), (18) длины которых суть 2 k и 2 n, при этом частичные суммы второй последовательности положительны. Обратно, имея две сбалансированные последовательности (18) длин 2 k и 2 n,

можно составить из них сбалансированную последовательность (17) длины n. Если вторая из последовательностей (18) имеет положительные частичные суммы, то последней нулевой частичной суммой последовательности (17) окажется частичная сумма с номером 2 k. По правилу произведения число последовательностей (17), для которых последняя нулевая частичная сумма имеет номер 2 k, составляет Ck ⋅ Cn – k –1.

Таким образом, суммируя по всем k < n и учитывая, что

C 0 = 1, приходим к равенству

Cn = C 0 Cn –1 + C 1 Cn –2 + … + Cn –1 C 0. (19)

В частности,

C 1 = C 02 = 1; C 2 = C 0 C 1 + C 1 C 0 = 2;

C 3 = C 0 C 2 + C 1 C 1+ C 2 C 0 = 5; ….

Составим производящую функцию:

C (z) = C 0 + C 1 z + C 2 z 2 + ….

Используя (19), получаем:

C (z)2 = C 02 + (C 0 C 1 + C 1 C 0) z + (C 0 C 2 + C 1 C 1+ C 2 C 0) z 2 … =

= C 1 + C 2 z + C 3 z 2 + ….

Умножая обе части последнего равенства на z и добавляя 1,

приходим к соотношению

z ⋅ C (z)2 +1 = C (z).

Таким образом, y = C (z) удовлетворяет квадратному уравнению

z ⋅ y 2 – y +1 = 0.

Решая его, находим:

y  1

2 z

1 

1 − 4 z 

Для функции y = C (z) должно выполняться соотношение

lim C (z)  1. Для

z →0

y  1

2 z

1 

1 − 4 z 

предел при z →0 не

существует. Следовательно,

C (z)  1

2 z

1 −

1 − 4 z .

Воспользовавшись биномом Ньютона, находим:

1  1/ 2  

1/ 2 

C (z) 

1− ∑ 

(−4 z) k  

∑ (−1) k −1

⋅22 k −1 zk −1,

т.е.

2 z 

k ≥0  k 

 k ≥1

 k 

 1/ 2 

C (z) 

∑ (−1) k 

⋅22 n 1 zn.

Таким образом,

n ≥ 0

 n 1

C  (−1) k  1/ 2 ⋅22 n 1.

 

n  n 1



Несложно проверить, что

 1/ 2 



1 2 n 

(−1) k 

⋅22 n 1 

 .

 n 1

Окончательно получаем:

n 1 n 

1 2 n 

Cn 



n 1

. (20)

n 

Числа Cn называются числами Каталана. Числа Каталана часто встречаются при решении задач перечисления (см. далее перечисление бинарных деревьев).

Формула (20) позволяет установить и некоторые другие факты о числе путей.

Для начала напомним, что при выводе (20) мы пришли к заключению, что число сбалансированных последовательностей длины 2 n с положительными частичными суммами равно Cn –1.

Любая последовательность (17) с положительными

частичными суммами после умножения на –1 превращается в последовательность с отрицательными частичными суммами и обратно. Следовательно, число последовательностей (17) с отрицательными частичными суммами и нулевой суммой s 2 n столько же, сколько и сбалансированных последовательностей с положительными частичными суммами, т. е. Cn –1. Таким образом, число последовательностей (17), для которых s 2 n = 0 и ни одна частичная сумма не обращается в ноль, равно 2 Cn –1.

Если пути на биномиальной решетке соответствует

последовательность (17) такая, что s 2 n = 0, а все частичные суммы отличны от нуля, говорят, что первое возвращение в ноль происходит в момент 2 n.

Сумма

t

∑ 2 Ck −1 = 2 C 0 + 2 C 1 +…+ 2 Ct –1

k 1

дает число путей, на которых первое возвращение в ноль происходит в один из моментов 2, 4, …, 2 t. Соответственно

t

22 t – ∑ 2 Ck −1–

k 1

это число путей длины 2 t, для которых возвращения в ноль до момента 2 t (включая его) не происходит. Из них половина путей расположена выше нулевого уровня, а половина – ниже. Следовательно, количество путей, для которых число повышений превосходит число понижений в любой момент

времени от 1 до 2 t, равно

22 t –1 –

t

∑ Ck −1.

k 1

Анализ (как правило, довольно сложный) подобного рода величин позволяет оценить вероятность того или иного варианта развития событий, связанных с изменением цены актива.

Числа Фибоначчи

Не нашли, что искали? Воспользуйтесь поиском: