Биномиальный ряд. Производящие функции

Степенные ряды

Хотя название «бином Ньютона» и закрепилось за формулой

(x  y) n 

n

k  0

истинная заслуга Ньютона состоит в том, что ему удалось обобщить формулу (1) на случай произвольных показателей степени. Изучением этого обобщения мы займемся в п. 10.2. Ниже излагаются необходимые сведения о степенных рядах.

Формальным степенным рядом (от переменной z)

называется выражение вида

∞

∑ ak z k, (2)

k  0

где ak – члены числовой последовательности, называемые коэффициентами степенного ряда (2). Символ суммирования в (2), вообще говоря, формальный. Тем не менее (2) записывают также в виде

a 0 + a 1 z + a 2 z 2 + a 3 z 3 +….

Пусть даны формальные ряды

∞

∑ ak z k

k  0

∞

и ∑ bk z k. (3)

k  0

Их суммой по определению является ряд

∞

∑ (ak k  0

 bk) z k.

Произведением рядов (3) называется ряд

∞

∑ сk z k,

k  0

такой, что

ck = a 0 bk + a 1 bk –1 +…+ akb 0

для всех k = 0, 1, 2,…. Заметим, что коэффициенты ck получаются так, как если бы в произведении рядов были раскрыты скобки и приведены подобные:

(a 0 + a 1 z + a 2 z 2 +…)(b 0 + b 1 z + b 2 z 2 +…) =

= a 0 b 0 + (a 0 b 1 + a 1 b 0) z + (a 0 b 2 + a 1 b 1 + a 2 b 0) z 2 +…

Производная ряда (2) определяется как ряд

a 1 + 2 a 2 z + 3 a 3 z 2 +….

Несложно проверить, что так определенные сложение, умножение и дифференцирование рядов обладают привычными свойствами. Сложение и умножение ассоциативны и коммутативны, сложение дистрибутивно относительно умножения. Производная суммы равна сумме производных. Справедливо также соотношение (uv)′ = u ′ v + uv ′.

Говорят, что ряд (2) сходится при z = t, где t – некоторое

числовое значение, если существует предел

lim

n

∑ ak t k. (4)

n →∞ k  0

Предел (4) в случае, когда он существует, называют суммой

∞

ряда при z = t и обозначают ∑ ak t k.

k  0

Любой степенной ряд сходится при z =0. Суммой ряда (2) в нуле является число a 0. Если ряд сходится при z = t 1, то он сходится и при любом z = t 2, для которого | t 2| < | t 1|. Таким образом, если степенной ряд сходится в некоторой точке, отличной от нуля, то он сходится во всех точках некоторого открытого промежутка вида (– r, r), где r ∈(0; +∞]. На промежутке, в точках которого ряд сходится, его сумма задает

функцию. Пишут

f (z) 

∞

∑ ak z k,

k  0

имея в виду, что ряд в правой части сходится в некоторой окрестности нуля, и в каждой точке t из этой окрестности

∞

выполняется равенство

f (t) 

∑ ak t k.

k  0

Пример. Ряд

1 + z + z 2 + z 3 + …

сходится во всех точках промежутка (–1, 1). В каждой точке t ∈(–1, 1) этот ряд представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем t. В

соответствии с известной формулой

1 + z + z 2 + z 3 + … =

1. (5)

1 − z

∞

Если степенные ряды ∑ ak z k

k  0

∞

и ∑ bk z k

k 0

сходятся в

некоторой общей точке, то в этой точке сходятся их сумма и

∞

произведение; если степенной ряд

∑ ak z k k  0

сходится в

некоторой точке, отличной от нуля, то в этой точке сходится и

его производная. Пусть,

Тогда:

f (z) 

∞

∑ ak z k;

k  0

g (z) 

∞

∑ bk z k.

k  0

 ∞   ∞ 

 ∑ ak z k    ∑ bk z k  

f (z)  g (z);

 k 0

  k 0 

 ∞  ∞ 

 ∑ ak z k  ∑ bk z k  

f (z) g (z);

 k 0

 k 0 

∞

∑ kak z k −1 

k 1

f ′(z).

Биномиальный ряд

Начнем с того, что запишем формулу (1) в виде

(1  z) n 

 n  k

∑   z

k

(6)

k ≥0 

трактуются как биномиальные коэффициенты,

 n 

обычно используется обозначение 

).

 k 

Заменяя в формуле (5) z на – z, получаем:

1 – z + z 2 – z 3 + … =

1. (7)

1  z

По аналогии с (7) запишем последнее соотношение в виде

 − 1

(1  z)−1 

Сравнивая (7) и (8), получаем:

∑ 

k ≥ 0  k

 z k. (8)



 − 1

 − 1

Вообще,

   1; 

 0  

  −1, ….

1 

   (−1).

 

Возьмем производную от обеих частей равенства (8):

 − 1

− (1  z)−2 

∑ k 

 z k −1.

Полагая

 − 2 

 − 1

k ≥1

 − 2 

 k 

 − 1 

   −

; …; 

  −(k  1) ⋅

; …,

 0 

 1 

 k 

 k  1

получаем равенство

 − 2 

(1  z)−2

 ∑ 

k ≥0 k

 z k.



Продолжая подобным образом, мы будем получать

равенства вида

 − n 

(1  z)− n

 ∑ 

k ≥ 0  k

 z k. (9)



Чтобы получить рекуррентные соотношения, связывающие биномиальные коэффициенты, продифференцируем обе

части (9):

 − n 

− n (1  z)−(n 1) 

∑ k 

 z k −1.

Следовательно,

k ≥1  k 

k  − n 

k  1 

− n 

(1  z)−(n 1)  ∑ − 

 z k −1  ∑ −

  z k.

k ≥1

n  k 

k ≥ 0

n  k  1

Сравнивая это равенство с равенством вида (9) для

показателя n + 1, приходим к следующему соотношению:

 − (n  1) 

k  1 

− n 

   −

 . (10)

 k 

n  k  1

Используя (8) и (10) и применяя метод математической

индукции, нетрудно придти к следующему заключению:

 − n 

k n (n  1) ⋅K⋅(n  k − 1)

k C k

   (−1)

 k 

 (−1)

n  k −1. (11)

Равенство (11) можно записать в следующем виде:

  

⋅(− n − k  1). (12)

 

Формулу для числа сочетаний и (12) можно свести в одну общую формулу:

  , (13)

 

 k  k!

 

где  – положительное или отрицательное целое число.

На самом деле в качестве  можно взять любое

действительное число. При этом справедливо соотношение

 б 

 б 

 б 

(1  z)б

 1  

 z  

 z 2  

 z 3 .... (14)

 1 

 2 

 3 

Чтобы из (14) получить (13) достаточно продифференцировать k раз обе части равенства (14) и

подставить z =0:

 б 

 б 

б(б − 1)K(б − k  1)(1  z)б − k

 k!

  (k  1)!

 z  K;

 k 

 б 

 k  1

б(б − 1)K(б − k  1)  k! k .

 

Пример. Покажем, что

 

 k 

 1 2   (−1) k  2 

(k  1)22 k 1. (15)

 k  1

 k 

   

В соответствии с (13) имеем:



  1 2 (1 2 − 1) ⋅K⋅(1 2 − k)  (−1) k 1⋅1⋅3 ⋅K⋅(2 k − 1).

 k  1

(k  1)!

2 k 1(

 1)!

  k

Умножив числитель и знаменатель последней дроби на

2 ⋅ 4 ⋅⋅ 2 k = 2 k ⋅ k!,

получаем доказываемое соотношение:

 1 2



(2 k)!

 (−1) k

1 (2 k)!.

22 k 1 k!(k  1)!

22 k 1(k  1)

k! k!



Используя предыдущую формулу, вычислим начальные

коэффициенты разложения в ряд функции (1 + z)1/2. Получаем:

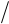1 2 

1 2 

1 1 2 

1 1 2 

1 1 2  5

   1; 

 0  

 ; 

1  2 

  −; 

2  8 

 ; 

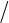3  16 

  −.

4  128

Таким образом,

1  z

 1  1 z − 1 z 2  1 z 3 − 5 z 4  K.

2 8 16

Не нашли, что искали? Воспользуйтесь поиском: