
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производящие функции линейных рекуррентных последовательностей
Наша ближайшая цель – определить, какой вид имеет производящая функция произвольной линейной рекуррентной последовательности.
Рассмотрим в качестве примера производящую функцию последовательности чисел Фибоначчи:
F (z) = F 0 + F 1 z + F 2 z 2 + …. (4)
Умножим F (z) на z и на z 2:
zF (z) = F 0 z + F 1 z 2 + F 2 z 3 + …;
z 2 F (z) = F 0 z 2 + F 1 z 3 + F 2 z 2 + ….
Так как F 2 = F 1 + F 0; F 3 = F 2 + F 1;…, то
zF (z) + z 2 F (z) = F 0 z + F 2 z 2 + F 3 z 3 + ….
Учитывая, что F 0 = 0 и F 1 =1, получаем:
z + zF (z) + z 2 F (z) = F (z).
Отсюда получается компактная формула:
 F (z) = z. (5)
F (z) = z. (5)
1 − z − z 2
Используя (5), можно найти явные выражения для чисел
Фибоначчи. Начнем с того, что представим дробь из (5) в виде
Тогда
z
1 − z − z 2
A
= A +
1 − б z
n
B


 1 − в z
1 − в z
 B
B
. (6)
n
 1 − б z
1 − б z
A ∑ (б z)
n ≥ 0
;
1 − в z
B ∑ (в z),
n ≥ 0
и, значит,
z
= A ∑(б z) n + B ∑(в z) n = ∑(A б n B в n) z n.
1 − z − z 2
 n ≥ 0
n ≥ 0
n ≥ 0
n ≥0
Таким образом,
Fn = A n + B n.
Чтобы найти неизвестные коэффициенты A, B, и , приведем дроби из (6) к общему знаменателю и приравняем коэффициенты при одинаковых степенях z. Получаются следующие уравнения:
+ = 1; = –1; A + B = 0; A + B = –1.
 Решая полученную систему, находим:
Решая полученную систему, находим:

 б 1
б 1
5; в 1 −
 2
2
5; A =
1; B = − 1.

 5 5
5 5
Окончательно получаем:
 1 1 5 n
1 1 5 n
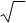
|
5
 Fn
Fn
|
Пусть теперь
−
|
2 . (7)
u 0, u 1, u 2,… – (8) произвольная рекуррентная последовательность, удовлетворяющая соотношению
un + r = a 1 un + r –1 + a 2 un + r –2 +…+ arun, (9)
и
f (z) = u 0 + u 1 z + u 2 z 2 +… –
ее производящая функция. Рассмотрим произведение f (z) на
многочлен
h (z) = 1 – a 1 z – a 2 z 2 –…– arzr.
Коэффициент при zn + r равен
un + r – a 1 un + r –1 – a 2 un + r –2 –…– arun,
и, значит, обращается в ноль в силу (9). Таким образом, в произведении h (z) f (z) все коэффициенты при степенях z, больших или равных r, обращаются в ноль, т. е. g (z) = h (z) f (z) – это многочлен степени не выше чем r – 1. Производящая функция последовательности (8) оказывается равной дробно-
рациональной функции
f (z)
 g (z).
g (z).
h (z)
 Примеры. 1. Для геометрической прогрессии со знаменателем q имеем
Примеры. 1. Для геометрической прогрессии со знаменателем q имеем
f (z) = u 0 + u 0 qz + u 0 qz 2 +…; h (z) = 1 – qz; h (z) f (z) = u 0,
откуда получается хорошо известная формула:
f (z)
u 0.
1− qz
2. Пусть теперь u 0, u 1, u 2,… – арифметическая прогрессия.
Так как un +2 = 2 un +1 – un, то
h (z) = 1 – 2 z + z 2
и
Следовательно,
h (z) f (z) = u 0 + (u 1 – 2 u 0) z 2.
 f (z) u 0 (u 1 − 2 u 0) z. (10) (1 − z)2
f (z) u 0 (u 1 − 2 u 0) z. (10) (1 − z)2
Рассмотрим, в частности, последовательность положительных целых чисел 1, 2, 3, …. Запишем ее производящую функцию:
f (z) = 1 + 2 z + 3 z 2 + …. (11)
По формуле (10) получаем:
f (z)
 (1− z)2
(1− z)2
. (12)
К тому же результату можно придти по-другому. Ряд (11)
получается как производная ряда
z + z 2 + z 3+ …,
сумма которого (как сумма геометрической прогрессии) равна
z
 1− z
1− z
. (13)
Дифференцируя (13), получаем (12).
Наряду с многочленом h (z) рассмотрим многочлен
k (z) = zr – a 1 zr –1 – a 2 zr –2 –…– ar,
называемый характеристическим (для последовательности, члены которой удовлетворяют рекуррентному соотношению (1)).
Многочлены h (z) и k (z) связаны простым соотношением:
h (z) = zrk (1/ z).
Пусть 1, 2, …, s – корни характеристического многочлена
(возможно, комплексные) с кратностями p 1, p 2, …, ps. Тогда
k (z) (z − б1
и, соответственно,
) p 1 (z − б 2
) p 2 K(z − б s
) ps,
h (z) (1−б1
z) p 1 (1− б2
z) p 2 K(1− б s
z) ps.
Рациональная функция
f (z)
g (z)
 h (z)
h (z)
может быть представлена в
виде суммы простых дробей вида
в
 (1− б z) p
(1− б z) p
, (14)
где = i – один из корней характеристического многочлена, p
лежит в промежутке от 1 до pi, а – некоторое число.
Разлагая (14) по формуле бинома, получаем:
в − p
n n n
 (1 б z) p
(1 б z) p
∑в
(−1) б z.
n
−
Относительно n выражение
n ≥ 0
− p n n n
n n p −1
(−1)
n
(−1)
C p n −1 ⋅(−1)
C p n −1 C p n −1
является многочленом степени не выше p – 1 и, тем более, не выше pi – 1. Следовательно, сумма всех дробей вида (14),
относящихся к одному и тому же корню = i, может быть
представлена в виде
∑ P (n)б nzn, причем степень многочлена
i i
n ≥0
Pi (n) не превышает pi – 1. Суммируя по всем i = 1, 2, …, s,
получаем:
s n n
f (z)
∑ ∑ Pi (n) i z.
n ≥ 0 i 1
Сравнивая полученное выражение с
f (z) = u 0 + u 1 z + u 2 z 2 +…,
приходим к заключению, что
s
un ∑
i 1
|
. (15)
Пример. Рассмотрим последовательность 6, 0, 12, …,
удовлетворяющую рекуррентному соотношению
un +3 = 3 un +1 + 2 un.
Многочлен
k (z) = z 3 –3 z – 2
является характеристическим для этой последовательности.
Раскладывая его на множители получаем:
k (z) = (z + 1)2(z – 2).
Следовательно, члены рассматриваемой последовательности имеют вид
un = P (n)⋅(–1) n + Q ⋅2 n,
где P (n) – многочлен степени не выше первой, а Q – степени не выше нулевой (т. е. ноль или некоторое число).
Будем искать un в виде
un = (An + B)⋅(–1) n + Q ⋅2 n.
Поскольку u 0 = 6, u 1 = 0, u 2 = 12, получаем следующие уравнения относительно A, B и Q:
B + Q = 6; –(A + B) + 2 Q = 0; 2 A + B + 4 Q = 12.
Решая систему, находим:
Следовательно,
A = 0; B = 4; Q = 2.
un = (–1) n ⋅4 + 2 n +1.
Пример. Используя (15), найдем формулу для суммы квадратов первых n натуральных чисел.
Суммы квадратов связаны рекуррентным соотношением
sn +4 = 4 sn +3 – 6 sn +2 + 4 sn +1 – sn. Характеристический многочлен последовательности сумм квадратов
k (z) = z 4 – 4 z 3 + 6 z 2 – 4 z +1 = (z – 1)4
имеет единственный корень 1 кратности четыре.
Следовательно, sn представимо в виде
sn = An 3 + Bn 2 + Cn + D.
Так как
то
s 0 = 0, s 1 = 1, s 2 = 5, s 3 = 14,
D = 0; A + B + C = 1;
8 A + 4 B + 2 C = 5; 27 A + 9 B + 3 C = 14.
Вычисляем определитель системы уравнений, содержащих неизвестные A, B, C, и определители, соответствующие переменным:
1
∆ 8
1 1
4 2 −12;
1
|
1 1
|
|
|
14 9
1
∆ B 8
1 1
5 2 −6; ∆ С
1
|
1 1
|
|
|
27
9 14
Находим: A = 1/3; B = 1/2; C = 1/6. Следовательно,
s 1 n 3 1 n 2 1 n n (n 1)(2 n 1).
 n 3 2 6 6
n 3 2 6 6
Не нашли, что искали? Воспользуйтесь поиском: