Равносильность формул логики высказывания. Законы логики. Выражение импликации и эквиваленции через конъюнкцию, дизъюнкцию и отрицание

1.

Понятие множества — является одним из тех фундаментальных понятий математики, которым трудно дать точное определение, используя элементарные понятия. Поэтому ограничимся описательным объяснением понятия множества.

Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое. Создатель теории множеств Георг Кантор давал следующее определение множества — «множество есть многое, мыслимое нами как целое».

Высказывания и логические связки

Отдельные объекты, из которых состоит множество, называются элементами множества.

Множества бывают конечные и бесконечные. Множества называются конечным, если число его элементов конечно, т.е. если существует натуральное число n, являющееся числом элементов множества. А={a₁, a₂,a ₃,..., a_n}. Множество называется бесконечным, если оно содержит бесконечное число элементов. B={b₁,b₂,b₃,...}. Например, множество букв русского алфавита — конечное множество. Множество натуральных чисел — бесконечное множество.

Пустое множество — множество, не содержащее ни одного элемента — ∅. Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и тоже множество. Множества не равны X ≠ Y, если в Х есть элементы, не принадлежащие Y, или в Y есть элементы, не принадлежащие Х. Символ равенства множеств обладает свойствами:

• Х=Х; — рефлексивность
• если Х=Y, Y=X — симметричность
• если X=Y,Y=Z, то X=Z — транзитивность.

Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество.

Счетное множество — это такое множество А, все элементы которого могут быть занумерованы в последовательность (м.б. бесконечную) а₁, а₂, а₃,..., а_n,... так, чтобы при этом каждый элемент получил ишь один номер n и каждое натуральное число n было бы в качестве номера дано одному и лишь одному элементу нашего множества.Множество, эквивалентное множеству натуральных чисел, называется счетным множеством.

2. Для произвольных множеств А, В, и С справедливы следующие соотношения (табл. 1):

Таблица 1

1. Коммутативность объединения	1’. Коммутативность пересечения
2. Ассоциативность объединения	2’. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
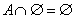
5. Закон идемпотентности объединения	5’. Закон идемпотентности пересечения
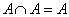
6. Закон де Моргана	6’. Закон де Моргана
7. Закон поглощения	7’. Закон поглощения
8. Закон склеивания	8’. Закон склеивания
9. Закон Порецкого	9’. Закон Порецкого
10. Закон двойного дополнения

3.

Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то, и другое вместе. Высказывания в математической логике обычно обозначаются прописными латинскими буквами: , , и т. д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - Логические связки. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит, указать, в каких случаях оно истинно, а в каких ложно. Отрицание — это высказывание, которое получается из данного высказывания с помощью слова «Не». Отрицание можно обозначать по-разному: , , . Отрицанием высказывания называется такое высказывание, которое принимает значение (ложно), если высказывание истинно, и значение (истинно), если высказывание ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, = «Завтра Не пойдет дождь». Дизъюнкция - Это высказывание, которое получается из двух Данных высказываний и с помощью союза «или». Дизъюнкция Обозначается . Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция истинна, когда истинно, по крайней мере, одно из высказываний и или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны. Конъюнкция - это высказывание, которое получается из двух данных высказываний и с помощью союза «и». Конъюнкция обозначается . Конъюнкция справедлива в том и только в том случае, когда оба высказывания истинны. Импликация Образуется из высказываний и с помощью слов «если... то...». Получается высказывание вида «если то ». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается. На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если , то » предполагает между и отношение посылки и следствия, или же причины и обусловленного ею действия. В логике импликация связывает любые два высказывания. Эквиваленция образуется из высказываний и с помощью слов «...тогда и только тогда, когда...»: Утверждение « тогда и только тогда, когда » не означает в логике, что составляющие высказывания и имеют одно и то же значение или один и тот же смысл.

4.

Законы логики

1) Идемпотентность дизъюнкции и конъюнкции:
, .

2) Коммутативность дизъюнкции и конъюнкции:
.

3) Ассоциативность дизъюнкции и конъюнкции:

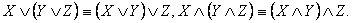
4) Дистрибутивность операций дизъюнкции и конъюнкции относительно друг друга:

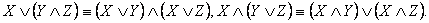
5) Двойное отрицание:
.

6) Закон де Моргана:

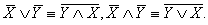
7) Склеивание:

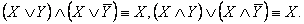
8) Поглощение:

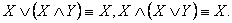
9) Действие с логическими константами 0 и 1:

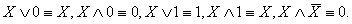
10) Закон исключения третьего:

11) Тождество:

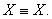
12) Отрицание противоречия:

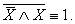
13) Контрапозиция:

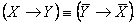
14) Цепное заключение:

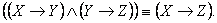
15) Противоположность:

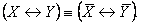
16) Модус поненс (modus ponens):

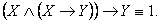
5.

Равносильность формул логики высказывания. Законы логики. Выражение импликации и эквиваленции через конъюнкцию, дизъюнкцию и отрицание

Формула F₁ равносильна формуле F₂, если при любых наборах входящих в них переменных формулы принимают одинаковые значение истинности.

Формула F₁ равносильна формуле F₂, если их эквиваленция есть тавтология, или , если - тавтология.

Свойства равносильности:

1) Рефлексивность ( )

2) Симметричность (Если , то )

3) Транзитивность ( )

6.

Законы де Моргана:

1.

2.

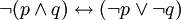
Закон контрапозиции:

1.

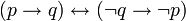
Законы поглощения:

1.

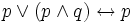
2.

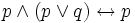
Законы дистрибутивности:

1.

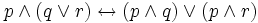
2.

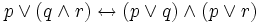
7. Рассуждения называют правильными, если из конъюнкции посылок следует заключение, т.е. всякий раз, когда все посылки истинны, заключение тоже истинно.

Пусть посылки, заключение. Тогда для определения правильности рассуждения по схеме , т.е. утверждения о том, что из данных посылок следует заключение , требуется установить тождественную истинность формулы .

Распространенными схемами правильных рассуждений являются следующие схемы: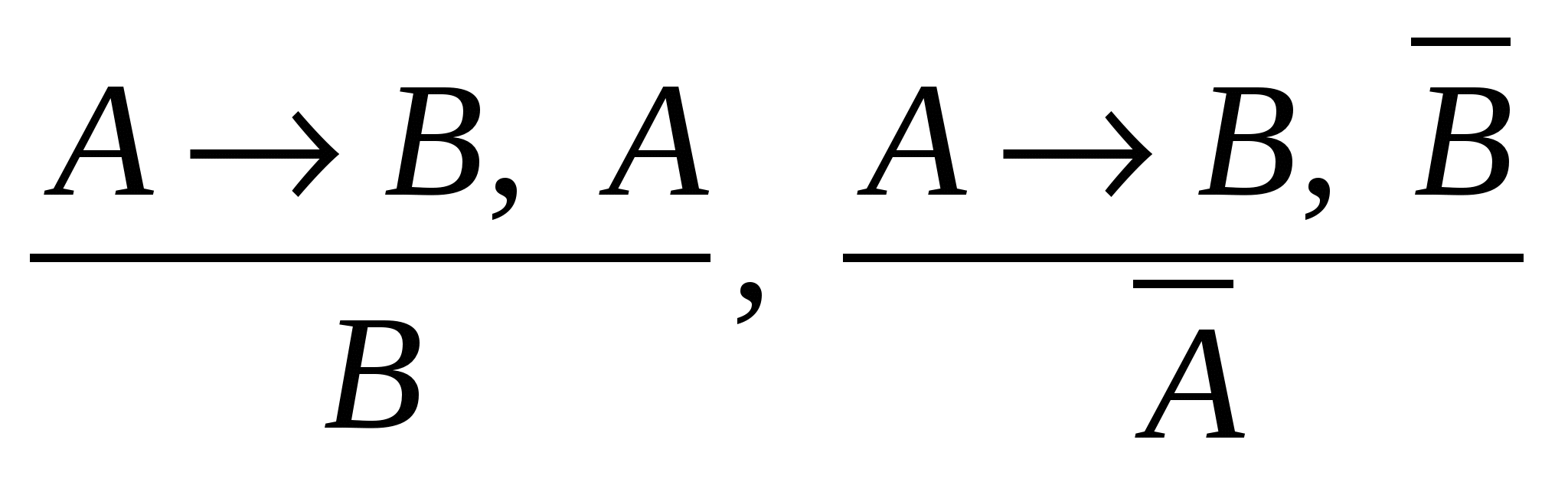

8.

Перестановками называют комбинации, состоящие из одних тех же различных элементов и отличающиеся только порядком их расположения.
Число всех возможных перестановок находится по формуле:
,
при этом, по определению, полагают, что .
Размещениями называют комбинации, составленные из различных элементов по элементов, которые отличаются либо составом элементов, либо их порядком.
Число всех возможных размещений вычисляется по формуле:
.
Сочетаниями называют комбинации, составленные из различных элементов по элементов, которые отличаются хотя бы одним элементом.
Число всех возможных сочетаний находится по формуле:
.
Число размещений, число перестановок и число сочетаний связаны формулой
.
При решении задач комбинаторики используют правила суммы и произведения.
Правило суммы. Если некоторый объект может быть выбран из совокупности объектов способами, а другой объект может быть способами, то выбрать либо , либо можно 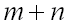способами.
Правило произведения. Если некоторый объект может быть выбран из совокупности объектов способами и после каждого такого выбора другой объект может быть выбран способами, то пара объектов в указанном порядке может быть выбрана способами.

9.

Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .

Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов по элементов обозначается через 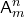(от начальной буквы французского слова “arrangement”, что означает размещение), где и .

Теорема. Число размещений множества из элементов по элементов равно

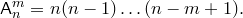
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

10.

Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

13.

Не нашли, что искали? Воспользуйтесь поиском: