Формула включения — исключения

Определение. Число элементов множества называется мощностью множества и обозначается .

Теорема. Пусть даны множества . Тогда количество элементов в объединении этих множеств можно найти по формуле:

Доказательство проводится по индукции. Пусть . Нужно доказать формулу

Действительно, множество состоит из всех элементов множества и тех элементов множества , которые не содержатся в множестве . Тогда, сложив количества элементов во множествах и , мы два
раза посчитаем количество элементов, общих для множеств и .

Предположим, что формула включения — исключения справедлива для множеств.
Докажем ее для множеств. Множество 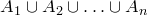можно представить в виде

Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):

Используя формулу

и формулу включения — исключения для множеств, получаем

В эту формулу подставляем выражение, полученное ранее, и теорема доказана.

15.

Пусть - непустое конечное множество. Обозначим через 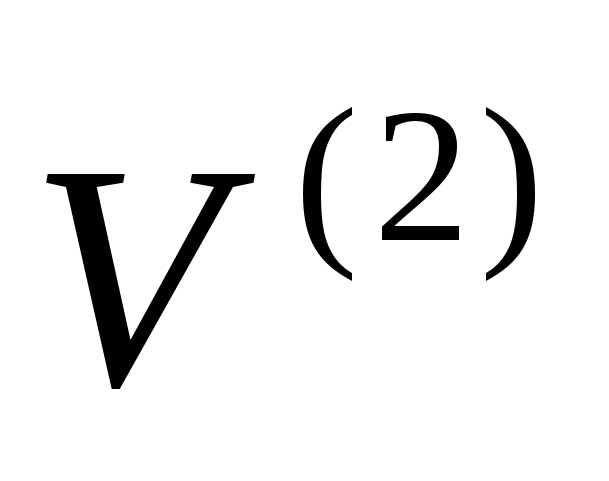множество всех его двухэлементных подмножеств (порядок элементов в двухэлементных подмножествах не имеет значения), т.е. .

1.
Пара , где – произвольное подмножество , называется графом (неориентированным графом). Элементы множества называются вершинами графа, а элементы множества – ребрами.

Итак, граф – это конечное множество вершин и множество ребер.
Множества вершин и ребер графа 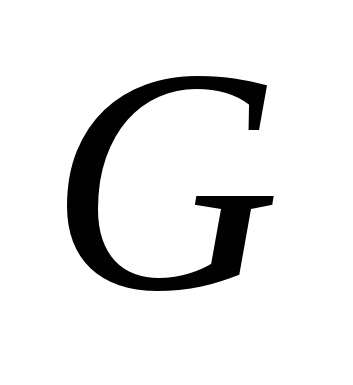будем соответственно обозначать и 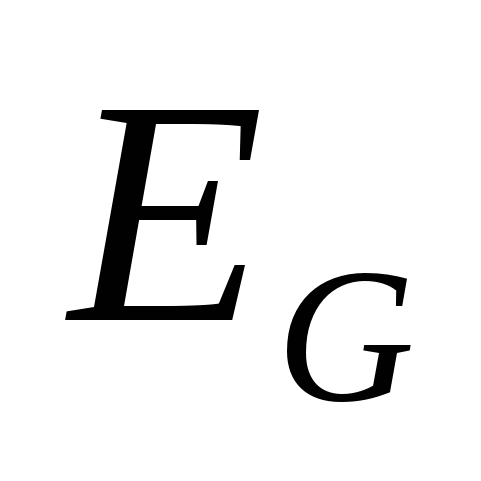. Вершины и ребра графа называются его элементами. Число вершин графа 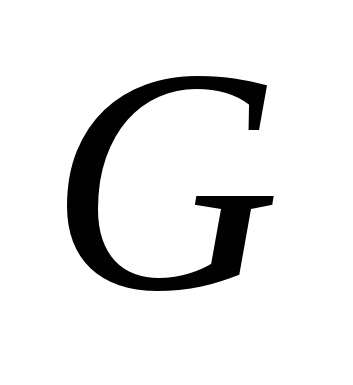называется его порядком и обозначается 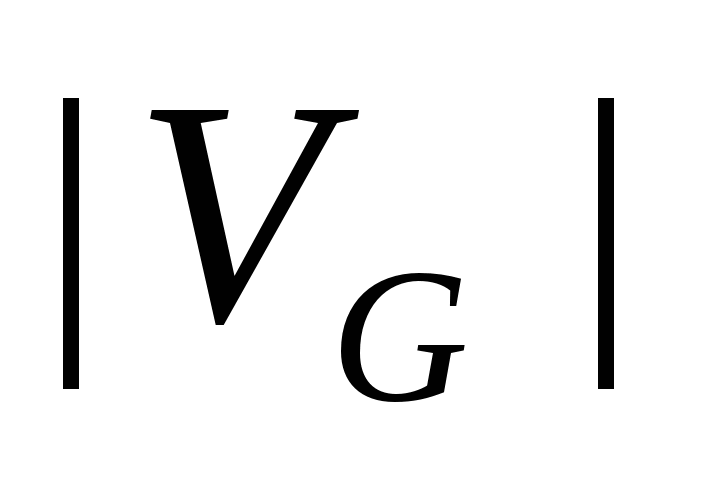. Если , , то граф 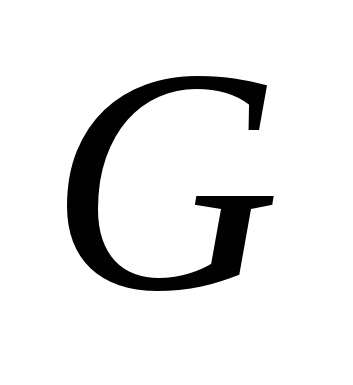называют 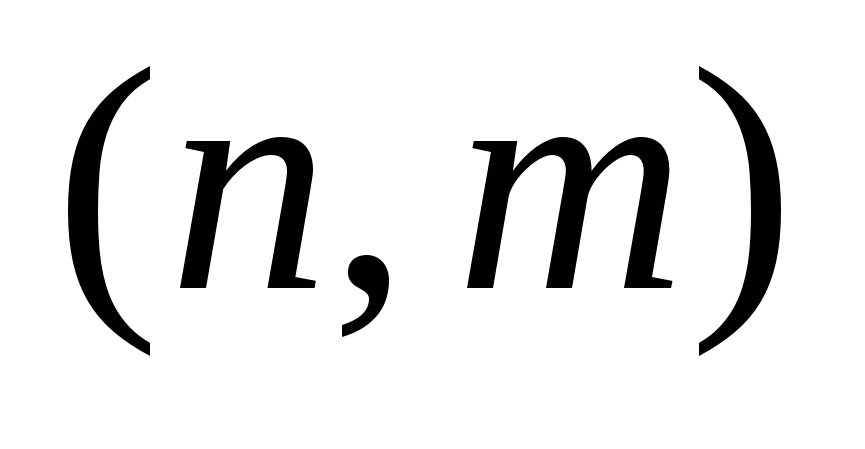–графом.

2. Говорят, что две вершины и 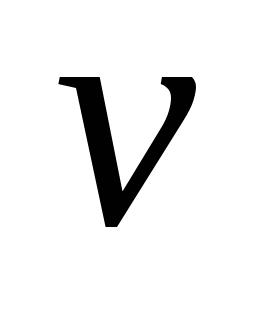графа смежны, если множество 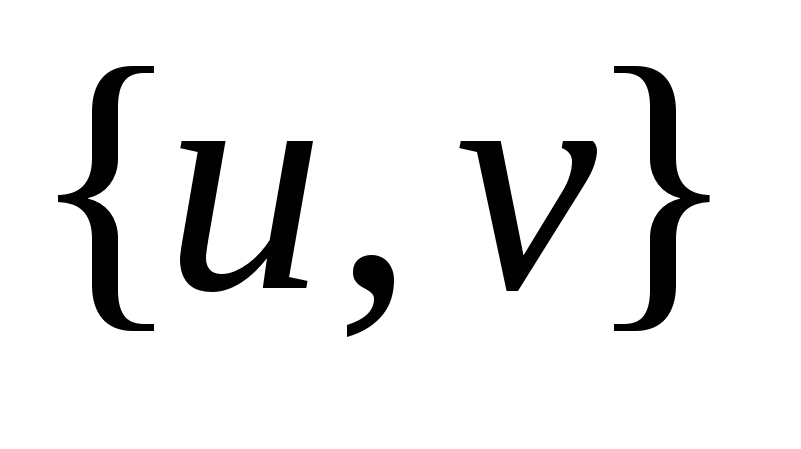является ребром, и не смежны в противном случае.

3. Если 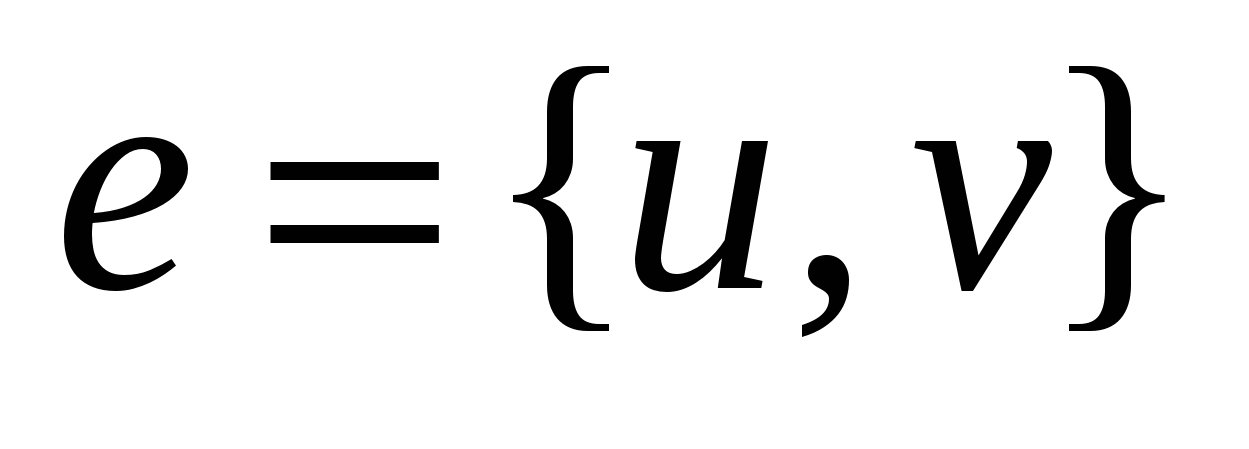– ребро, то вершины и 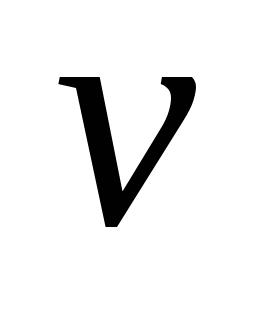называют его концами.

4. Два ребра называются смежными, если они имеют общий конец.

5. Вершина 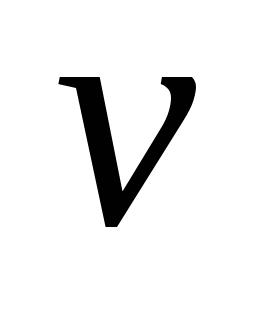и ребро 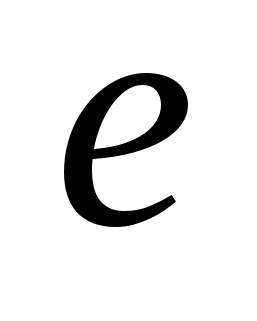называются инцидентными, если 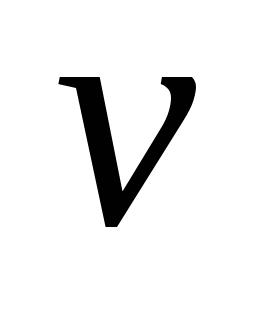является концом ребра .

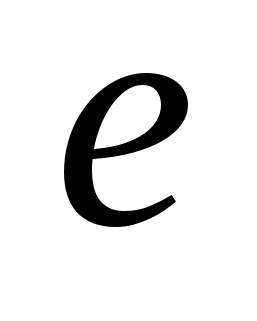6. Множество всех вершин графа 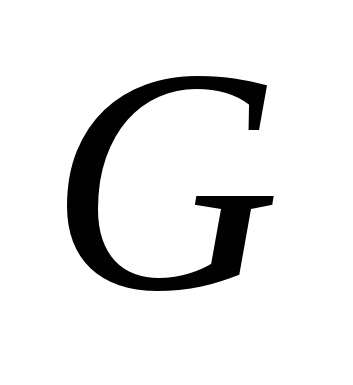, смежных с некоторой вершиной 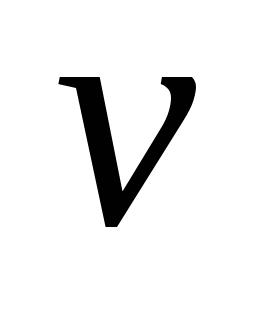, называется окружением вершины 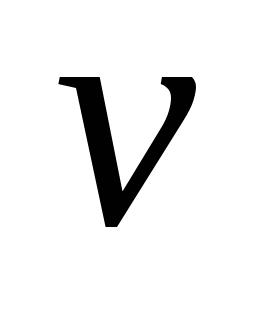и обозначается через .

7. Граф порядка называется помеченным, если его вершинам присвоены некоторые метки, например, номера 1,2,3,…, .

Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии – ребрам.

16.

Теория графов неоднократно переоткрывалась разными авторами при решении различных прикладных задач.
1.Начало теории графов относят к 1736 г., когда Эйлер решил популярную в то время задачу о кенигсбергских мостах (сегодня Калининград). Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку.

2. Задача о трех домах и трех колодцах. Имеется 3 дома и 3 колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эта задача была решена Куратовским в 1930г.

17.

Не нашли, что искали? Воспользуйтесь поиском: